আজকে আমরা আলোক তড়িৎ ক্রিয়া সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৮ এর আধুনিক পদার্থবিজ্ঞান এর অন্তর্ভুক্ত।
আলোক তড়িৎ ক্রিয়া
আলো তড়িৎ ক্রিয়া (Photo Electric Effect)
কোনো ধাতব পৃষ্ঠে উপযুক্ত তরঙ্গদৈর্ঘ্যের আলো ফেললে তার থেকে ইলেকট্রন নির্গত হয়। এই ঘটনাকে আলোক তড়িৎ ক্রিয়া বলে। আলো তড়িৎ ক্রিয়ায় নিঃসৃত ইলেকট্রনগুলোকে ফটোইলেকট্রন (Photoelectron) বলে।
উপযুক্ত ব্যবস্থার সাহায্যে ফটোইলেকট্রনগুলোর একমুখী স্রোত তৈরি করা যায়। এর ফলে যে তড়িৎ প্রবাহের সৃষ্টি হয় তাকে আলোতড়িৎ প্রবাহ ( Photoelectric current) বলে।
আলোক তড়িৎ ক্রিয়ার পরীক্ষা (Experiment of Photo Electric Effect)
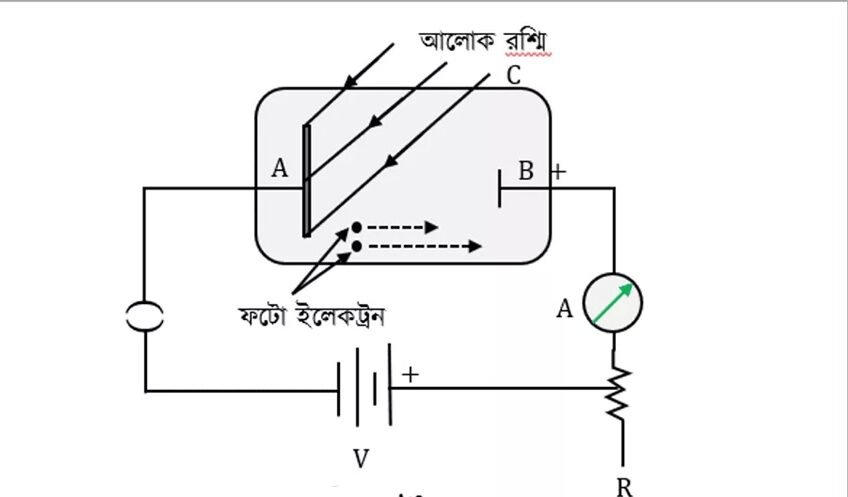
চিত্রে আলোক তড়িৎ ক্রিয়া পরীক্ষার যন্ত্রের দেখানো হয়েছে। আলো সংবেদনশীল ধাতব পাত A এবং এর বিপরীত পার্শ্বে অপর একটি ধাতব পাত B কে একটি বায়ু শূন্য কাচ নল C এর মধে রাখা হয়। পাতদুটি তড়িৎদ্বার হিসাবে কাজ করে এবং বিভব পার্থক্য সৃষ্টির জন্য ব্যাটারীর সাথে যুক্ত করা হয়। এই কাচ নলের সাথে হেলানো ভাবে যুক্ত কাচ নলের অপর মাথায় কোয়ার্জ (quartz) এর তৈরী জানালা D থাকে। আলোক উৎস S থেকে অতি বেগুনী রশ্মি জানালা D দিয়ে আলো সংবেদনশীল ধাতব পাত Aতে এসে পড়লে ফটোইলেকট্রন নির্গত হয়।
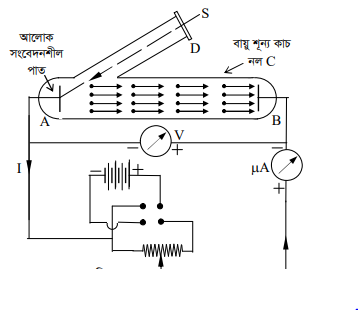
যখন A পাতের বিভব পার্থক্য (P.D) B পাতের তুলনায় ঋণাত্মক থাকে তখন A পাত থেকে নির্গত ফটো ইলেকট্রন ত্বরিত (accelerating) হয়ে B পাতের দিকে ধাবিত হয় ফলে আলো তড়িৎ প্রবাহ (Photo-electric current) | বর্তনীতে প্রবাহিত হয় এবং তা মাইক্রো অ্যামেটার [LIA দিয়ে মাপা হয়। দুই তড়িৎ-দ্বারের ত্বরান্বিত বিভব পার্থক্য ভোল্ট মিটার V দিয়ে মাপা হয় ।
যদি বিভব পার্থক্যকে বিপরীতমুখী করা হয় অর্থাৎ B পাতকে A পাতের তুলনায় ঋণাত্মক করা হয় তবে তড়িৎদ্বারে মন্দীভূত (retarding) বিভব পার্থক্যের কারণে ফটোইলেকট্রন B পাত দ্বারা বিকর্ষিত হয়ে A পাতের দিকে ফিরতে থাকবে ফলে আলো তড়িৎ প্রবাহ হ্রাস পাবে। মন্দীভূত বিভব বাড়াতে থাকলে এক সময় আলোক তড়িৎ প্রবাহের মান শূন্য হয়ে যাবে। এ বিভবকে নিবৃত্তি বিভব (stopping potential) vo বলে ।
আলোক তড়িৎ প্রবাহ নিম্নলিখিত বিষয়ের উপর নির্ভর করে ।
(ক) আপতিত বিকিরণের প্রাবল্য
(খ) আপতিত বিকিরণের কম্পাংক
(গ) দুই তড়িৎ দ্বারের বিভব পার্থক্য
(ঘ) ফটোইলেকট্রন নির্গতকারী পাতের প্রকৃতি।
আলো তড়িৎ ক্রিয়া পরীক্ষার সিদ্ধাড়
১। ধাতব পৃষ্ঠ থেকে প্রতি সেকেন্ডে নির্গত ফটোইলেকট্রনের সংখ্যা আপতিত বিকিরণের প্রাবল্যের সমানুপাতিক ।
২। স্থির কম্পাংকে কোন নির্দিষ্ট ধাতবের জন্য স্টপিং বিভব আপতিত বিকিরণের প্রাবল্যের উপর নির্ভরশীল নয়।
৩। কোন নির্দিষ্ট ধাতবের জন্য কম্পাংক বৃদ্ধির সাথে সাথে স্টপিং বিভব বা নিবৃত্তি বিভব বৃদ্ধি পায় ।
ধাতব পৃষ্ট থেকে নির্গত ফটো ইলেকট্রনের বেগ শূন্য থেকে সর্বোচ্চ একটা মানের মধ্যে সীমাবদ্ধ । স্টপিং বিভব Vo সর্বোচ্চ গতিশক্তি সম্পন্ন ইলেকট্রনকেও B পাতে পৌছাতে দেয় না। যদি e চার্জ বিশিষ্ট m ভরের ইলেকট্রন A পাত থেকে সর্বোচ্চ Vimax বেগে নির্গত হয় তবে ইলেকট্রনের সর্বোচ্চ গতি শক্তি 1/2 mv max = eVo । যে ইলেকট্রনগুলো এর চেয়ে কম বেগে 0 নির্গত হবে সেগুলো স্টপিং বিভব Vo এর চেয়ে কম মন্দীভূত বিভবে B পাতে যাওয়া বন্ধ হয়ে যায়।
পরীক্ষা লব্ধ ফলাফল থেকে আলো তড়িৎ প্রবাহ সম্পর্কিত বৈশিষ্ট্য সূচক সিদ্ধান্ত্ সমূহ
হলওয়াশ, স্টোলেটভ, লেনার্ড ও অন্যান্য বিজ্ঞানীরা পরীক্ষা লব্ধ ফলাফল থেকে নিম্নলিখিত সিদ্ধাড়ে উপনীত হন।
১। এটি একটি তাৎক্ষনিক ঘটনা। আলো আপতিত হওয়া ও ইলেকট্রন নির্গত হওয়ার মধ্যে সময়ের পার্থক্য শূন্য। (3×10 সেকেন্ড মাত্র)
২। আলোক তীব্রতা বৃদ্ধির সাথে সাথে কোন ধাতব তল থেকে প্রতি সেকেন্ডে নির্গত ফটো-ইলেকট্রনের সংখ্যা বৃদ্ধি পায়। কিন্তু নিৰ্গত ফটো-ইলেকট্রনের গতি শক্তি বৃদ্ধি পায়না।
৩। ধাতুর বৈশিষ্ট্যের উপর ভিত্তি করে নির্দিষ্ট সূত্রপাতকারী কম্পাংক (Thresold frequency) অতিক্রম না করা পর্যন্ত্ আলোক তীব্রতা যতই বৃদ্ধি করা হোক না কেন ধাতব তল থেকে কোনো ফটো-ইলেকট্রন নির্গত হয় না ।
৪। নির্দিষ্ট সূত্রপাতকারী কম্পাংক অতিক্রম করার পর কম্পাংক যতই বৃদ্ধি করা হয় নির্গত ফটো-ইলেকট্রনের গতিশক্তি ততই বৃদ্ধি পেতে থাকে ।
আলো তড়িৎ ক্রিয়া সম্পর্কিত যে বৈশিষ্ট্য সূচক সিদ্ধাগুলো পাওয়া যায় তাদের মধ্যে চিরায়ত বলবিদ্যার অসংগতি
তাড়িতচৌম্বক তরঙ্গ তত্ত্ব অনুসারে তরঙ্গ তলে তরঙ্গ শক্তি সমভাবে বন্টিত থাকে। বস্তুর ইলেকট্রন এই তরঙ্গ তলের খুব ক্ষুদ্র অঞ্চল জুড়ে সংস্পর্শে আসে। সুতরাং সেই অঞ্চল থেকে শক্তি শোষণ করে নিউক্লিয়াস থেকে বিচ্ছিন্ন হওয়ার মত প্রয়োজনীয় শক্তি সংগ্রহ করার জন্য যথেষ্ট সময় প্রয়োজন। কিন্তু আলোক-তড়িৎ ক্রিয়া একটি তাৎক্ষণিক ঘটনা। সুতরাং তাড়িতচৌম্বক তরঙ্গ তত্ত্ব অনুসারে আলোক তড়িৎ ক্রিয়ায় তাৎক্ষণিক ঘটনার ব্যাখ্যা দেয়া সম্ভব নয়।
ধাতব তল থেকে নির্গত ফটোইলেকট্রনের গতিশক্তি আলোর তীব্রতার উপর নির্ভরশীল নয় কম্পাংকের উপর নির্ভরশীল। তাড়িতচৌম্বক তরঙ্গ তত্ত্ব অনুসারে আলোক তীব্রতা বৃদ্ধির সাথে সাথে গতিশক্তি বৃদ্ধি পাবে যা পরীক্ষা লব্ধ ফলাফলের সাথে মিলে না।
ধাতুর বৈশিষ্ট্যের উপর ভিত্তি করে নির্দিষ্ট সূত্রপাতকারী কম্পাংকের নীচে যতই তীব্রতা থাকুক না কেন আপতিত আলোক তরঙ্গ ধাতব তল থেকে কোন ফটোইলেকট্রন নির্গত করতে পারে না। কিন্তু তাড়িতচৌম্বক তরঙ্গ তত্ত্ব অনুসারে যথেষ্ট প্রয়োজনীয় তীব্রতা থাকলে যে কোন কম্পাংকের আলোক তরঙ্গ ধাতব তল থেকে ফটোইলেকট্রন নির্গত করতে সক্ষম যা পরীক্ষা লব্ধ ফলাফলের অনুরূপ নয়।
পণ্ঢণ্ঢ্যাংকের কোয়ান্টাম তত্ত্ব ব্যবহার করে আইনস্টাইনের আলোক তড়িৎ ক্রিয়া ব্যাখ্যা
আইনস্টাইন আলোক তড়িৎ ক্রিয়ার ফলাফল পণ্ঢণ্ঢ্যাংকের কোয়ান্টাম তত্ত্বের উপর ভিত্তি করে যুক্তি সঙ্গত ব্যাখ্যা দেন । পণ্ঢণ্ঢ্যাংকের স্বীকার্য অনুযায়ী বিকিরণ ঝাঁক ঝাঁক কণার সমষ্টি। প্রতিটি কণার শক্তি E = hf । (এখানে h হলো পণ্ঢণ্ঢ্যাংকের ধ্রুবক যার মান 6.63×10-34Js এবং f হলো কম্পাংক) এই শক্তি অখন্ড এবং একে কোয়ান্টা বলে । বিকিরণ শক্তি শুধু কোয়ান্টা আকারে শোষিত বা নিঃসৃত হয় না, স্থানাড়রের সময়ও কোয়ান্টা আকারে প্রবাহিত হয়। শূন্য মাধ্যমে এর বেগ আলোর বেগের সমান। এই কোয়ান্টার নাম ফোটন।
এই জন্য এই তত্ত্বকে আইনস্টাইনের ফোটন তত্ত্বও বলে। তিনি প্রস্তাব করেন যে, একটি ফোটনের যখন কোনো পরমাণুর ইলেকট্রনের সাথে সংঘাত ঘটে সে সংঘাত সর্বদাই স্থিতিস্থাপক অর্থাং এই সংঘাতে কোন শক্তির অপচয় হয়না। এই সংঘাতের ফলে হয় ইলেকট্রনটি ফোটনের সমস্ড শক্তি শোষণ করে নতুবা কোনো শক্তি শোষণ করে না। সমড় শক্তি শোষণ করলে ইলেকট্রন hf শক্তি লাভ করে ।
পরমাণুর ইলেট্রনগুলো নিউক্লিয়াসের আকর্ষণে নিউক্লিয়াসের সাথে আবদ্ধ থাকে। সুতরাং ধাতুর পরমাণু থেকে ইলেট্রনকে মুক্ত করতে হলে নিউক্লিয়াসের এই আকর্ষণ বলের বির“দ্ধে কিছু কাজ সম্পন্ন করতে হয় অর্থাৎ কিছু শক্তি ব্যয়িত হয়। এই শক্তিকে ধাতুর আলোক-তড়িৎ কার্যাপেক্ষক (Work function) বলে। এই কাজের পরিমাণকে Wo দিয়ে নির্দেশ করা 0 হয়।
এখন ইলেকট্রনের ফোটন থেকে শোষিত শক্তি hf যদি কার্যাপেক্ষক W, এর চেয়ে কম হয় তবে ধাতু থেকে কোনো 0 ইলেকট্রন নির্গত হবে না। hf যদি Wo এর সমান হয় তবে শূন্য গতি শক্তি সম্পন্ন ইলেকট্রন নির্গত হবে এবং এই ইলেকট্রন নির্গত হয়ে ধাতুব পৃষ্ঠে অবস্থান করবে। আর hf যদি W, এর চেয়ে বেশী হয় তবে W, এর চেয়ে বেশী শক্তিটুকু ইলেকট্রনটি গতিশক্তি 2 0 হিসাবে লাভ করবে।
ধরা যাক, ফো’টন থেকে hf শক্তি গ্রহন করে m ভরের একটি ইলেকট্রন সর্বোচ্চ Vmax বেগে ধাতুর পৃষ্ঠ থেকে নির্গত হলো। তাহলে ইলেকট্রনটি সর্বোচ্চ = 1/2mv2max গতিশক্তি লাভ করবে। যদি ধাতুর আলোক-তড়িৎ কার্যাপেক্ষক W, তবে আমরা লিখতে পারি,
ফোটনের শক্তি, hf = Wo + 1/2mv2max ………………..(1)
একে আইনস্টাইনের আলো তড়িৎ তত্ত্বের সমীকরণ বলে। (৮.৫২) নং সমীকরণ থেকে লেখা যায়, ইলেকট্রনটি সর্বোচ্চ গতিশক্তি,
1/2mvmax2 = hf -Wo ………………..(2)
যে কম্পাংকের ফোটনের শক্তি শোষণ করে কোনো ধাতুর পৃষ্ট থেকে শূন্য গতি শক্তি সম্পন্ন ইলেকট্রন নির্গত হবে অর্থাৎ সম্পূর্ণ শোষিত শক্তিটি কার্যাপেক্ষক W এর জন্য ব্যয়িত হবে তাকে সূত্রপাতকারী কম্পাংক (Thresold frequency) বলে এবং একে fo দ্বারা প্রকাশ করা হয়।
অতএব, hfo = Wo ………………..(3)
(3) নং সমীকরণের মান (2) নং সমীকরণে বসালে,
hf -hfo = 1/2mv2max ………………..(4)
বা, h(c/λ – c/λo) = 1/2mv2max ………………..(5)
বা, hc(1/λ – 1/λo) = 1/2mv2max ………………..(6)
Vo নিবৃত্তি বিভব প্রয়োগ করলে কোনো ইলেকট্রন যদি ধাতব পৃষ্ঠ থেকে শূন্য গতিশক্তি নিয়ে নির্গত হয় তবে,
1/2mv2max = evo ………………..(7)
(5) ও (6) নং সমীকরণ থেকে লেখা যায়,
hc(1/λ – 1/λo) = eVo ………………..(8))
(3), (4), (5), (6), (7) ও (8) নং সমীকরণগুলো আইনস্টাইনের আলোক তড়িৎ ক্রিয়া সমীকরণের বিভিন্ন রূপ ।
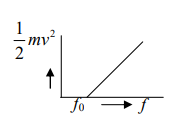
চিরায়ত বলবিদ্যার সাথে অসংগতিপূর্ণ অবস্থাগুলোর কোয়ান্টাম ধারণার সাহায্যে ব্যাখ্যা
আলোক তড়িৎ ক্রিয়ার পরীক্ষা থেকে প্রাপ্ত ফলাফল ব্যাখ্যায় চিরায়ত বলবিদ্যার সাথে অসংগতিপূর্ণ অবস্থাগুলো হলো- আলোক তড়িৎ ক্রিয়ায়,
১। আলোক তীব্রতার সাথে ইলেকট্রনের গতিশক্তির সম্পর্ক না থাকা,
২। সূত্রপাতকারী কম্পাংকের নীচের কম্পাংকে ইলেকট্রন নির্গত না হওয়া
৩। আলোক তড়িৎ ক্রিয়া একটি তাৎক্ষণিক ঘটনা।
চিরায়ত বলবিদ্যা ব্যাখ্যা দিতে অসমর্থ। আইনস্টাইনের আলোক তড়িৎ তত্ত্ব এগুলো সঠিক ব্যাখ্যা দেয়।
কোয়ান্টাম ধারণার সাহায্যে আলোক তড়িৎ ক্রিয়ার ব্যাখ্যা
১) কোয়ান্টাম তত্ত্ব অনুসারে, f কম্পাংক বিশিষ্ট বিকিরণ রশ্মির তীব্রতার অর্থ হলো প্রতি একক ক্ষেত্রফলের মধ্য দিয়ে প্রতি সেকেন্ডে লম্ব ভাবে অতিক্রমকারী hf শক্তি সম্পন্ন ফোটন সংখ্যা। তীব্রতা কখনই শক্তির উপর নির্ভরশীল নয়। সুতরাং তীব্রতা বৃদ্ধির সাথে সাথে প্রতি একক ক্ষেত্রফলে ফোটন সংখ্যার বৃদ্ধি । ফোটন সংখ্যা বৃদ্ধি পেলে সংঘাতকারী ইলেকট্রনের সংখ্যা বৃদ্ধি পাবে ফলে নির্গত ইলেকট্রনের সংখ্যা বাড়বে এবং নির্গত ইলেকট্রনের শক্তি পূর্বের মতই অপরিবর্তীত থাকবে।
২) কোয়ান্টাম তত্ত্ব অনুসারে, নির্দিষ্ট ধাতুপৃষ্ঠে সূত্রপাতকারী কম্পাংক (Thresold frequency) fo (যার শক্তি hfo) এসে পড়লে ইলেকট্রন নিউক্লিয়াস থেকে শুধু মাত্র শূন্য গতি শক্তি নিয়ে নির্গত হয়ে ধাতুপৃষ্ঠে অবস্থান করবে। আমরা Wo আইনস্টাইনের সূত্র থেকে লিখতে পারি 0 = hfo – Wo বা, fo । সুতরাং এর চেয়ে কম কম্পাংকের যত = h প্রাবল্যের (ফোটন ঘনত্বের) বিকিরণ আপতিত করা হোক না কেন ধাতুপৃষ্ঠ থেকে কোন ইলেকট্রন নির্গত হবে না ।
৩) কোয়ান্টাম তত্ত্ব অনুসারে f কম্পাংক বিশিষ্ট ফোটন (এখানে f> fo ধরা হয়েছে) hf শক্তি সম্পন্ন একটি কণার ন্যায় আচরণ করে। সুতরাং ফোটনটি ইলেকট্রনকে আঘাত করা মাত্রই (যেহেতু f> f0) ইলেকট্রনটি পরমাণু থেকে ছিটকে (কণার ধর্ম অনুসারে) বের হয়ে আসবে। সুতরাং এটি একটি তাৎক্ষণিক ঘটনা।
উদাহরণ ১:
একটি ধাতুর সূচন কম্পাঙ্ক 3.3×104Hz । যদি 8.2×104Hz কম্পাঙ্কের আলো ঐ ধাতুর উপর আপতিত হয় তবে ফটোতড়িৎ নিঃসরণে নিবৃত্ত বিভব কত হবে বের কর—ন।
সমাধান :
দেয়া আছে, vo =3.3×1014Hz, v = 8.2×104Hz এবং V = ?
আমরা জানি, E = hv=Wo+=1/2mv2 = hvo + 1/2mv2
বা, h(v-vo) =1/2mv2 = ev
বা, V = h(v-vo)/e
মান বসালে, V = 6.63 x10-34 x ( 8.2 x 1014 – 3.3×104 )/ 1.6×10-1 = 6.63×4.99/1.6 x 10 = 2.03V
উ: 2.03V
উদাহরণ ২:
কোনো পদার্থের কার্যাপেক্ষক 1.85 eV হলে ঐ পদার্থের সূচন কম্পাঙ্ক কত ?
সমাধানঃ
দেয়া আছে, Wo =1.85eV=1.85×1.6×10-19 J =2.96×10-19 J এবং fo =?
আমরা জানি,
কার্য অপেক্ষক, Wo = hfo
বা, fo = Wo/h
মান বসালে, fo = (2.96×10-19/6.63×10-34) = 4.465×10 4 Hz
উ: 4.465×104Hz
উদাহরণ ৩:
সোডিয়ামের কার্যাপেক্ষক 2.3eV । এর উপর 2000Å তরঙ্গদৈর্ঘ্যের আলোক রশ্মি আপতিত হলে নির্গত ইলেকট্রনের সর্বোচ্চ গতিশক্তি নির্ণয় করন।
সমাধানঃ
দেয়া আছে, Wo = 2.3ev = 2.3×1.6×109 J = 3.68×10 J
λo = 2000Å = 2000 x 10-10m এবং Ekmax = ?
আমরা জানি,
আইনস্টাইনের আলোক তড়িৎ সমীকরণ থেকে, hf = 1/2mv2 max + Wo = Ekmax + Wo
বা, Ekmax = hf – Wo = hC/λ – Wo
মান বসালে, Ekmax = 6.63×10-34 × (3×108/( 2000×10-10) -3.68×10-19
Ekmax = 6.63×10-34 x 15 x 10-14 -3.68×10-19
Ekmax = 9.95×10-19 -3.68×10-19 J
Ekmax = = 6.27×10-19J= (6.27×10-19)/( 1.6×10-19)eV = 3.92eV
উ: 3.92eV
উদাহরণ ৪:
কোন ধাতুর নিবৃতি বিভবের মান কত হলে ঐ ধাতু হতে নিঃসৃত 2000kms বেগে একটি ইলেকট্রন নিবৃত্ত হবে ?
সমাধানঃ
দেয়া আছে, v = 2000kms-1 = 1×106ms-1, me =9.11×10-31kg, e=1.6×10-19 C এবং Vo = ?
আমরা জানি,
1/2mv2 = eVo
বা, Vo = mv2/2e
মান বসালে, Vo = {9.1×10-31 ×(2×106)2}/( 2×1.6×10-19) =11.375V
উ: 11.375V
সার-সংক্ষেপ :
আলো তড়িৎ ক্রিয়া :
কোনো ধাতব পৃষ্ঠে উপযুক্ত তরঙ্গদৈর্ঘ্যের আলো ফেললে তার থেকে ইলেকট্রন নির্গত হয়। এই ঘটনাকে আলোক তড়িৎ ক্রিয়া বলে।
ফটোইলেকট্রন:
আলোতড়িৎ ক্রিয়ায় নিঃসৃত ইলেকট্রনগুলোকে ফটোইলেকট্রন বলে ।
আলোতড়িৎ প্রবাহ:
উপযুক্ত ব্যবস্থার সাহায্যে ফটোইলেকট্রনগুলোর একমুখী স্রোত তৈরি করা যায়। এর ফলে যে তড়িৎ প্রবাহের সৃষ্টি হয় তাকে আলোতড়িৎ প্রবাহ বলে ।
বহুনির্বাচনী প্রশ্ন:
নিচের অনুচ্ছেদটি পড়ো এবং ১ ও ২ নং প্রশ্নগুলোর উত্তর দাওঃ
4000° A তরঙ্গদৈর্ঘ্যের আলো কোনো ধাতব পৃষ্ঠে আপতিত হলে যে ইলেকট্রন নির্গত হয় তার সর্বোচ্চ গতিশক্তির মান 0.4eV ।
১. ধাতব পৃষ্ঠের উপর আপতিত ফোটনের শক্তি-
ক. 4.1078eV
খ. 2.7810eV
গ. 3.1078eV
ঘ. 1.30eV
২.ঐ ধাতুর কার্যাপেক্ষক-
ক. 2.70 ev
খ. 3.707 ev
গ. 3.5078 eV
ঘ. 4.3078 ev
