আজকে আমরা আলোর অপবর্তন ও সমবর্তন সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৭ ভৌত আলোকবিজ্ঞান এর অন্তর্ভুক্ত।

আলোর অপবর্তন ও সমবর্তন
আলোর অপবর্তন (Diffraction of light):
আমরা জানি শব্দ তরঙ্গ কোনো প্রতিবন্ধকের ধার ঘেঁষে বেঁকে যেতে পারে। কোনো ছিদ্রের মধ্য দিয়ে যাবার সময় চারিদিকে ছড়িয়ে পরে। আলোক তরঙ্গের ক্ষেত্রেও একই ঘটনা ঘটে। সূর্যরশ্মি অসীম থেকে আসে বলে আলোক রশ্মিগুলো সমাাল থাকে। সূর্যরশ্মিতে কোনো তীক্ষ্ণ ধার বিশিষ্ট টিনের পাত রেখে তার ছায়া কোনো দেয়ালে ফেলা হলো।
জ্যামিতিক আলোকবিজ্ঞান অনুসারে আলো সরলরেখায় চলে। সুতরাং তীক্ষ্ণ ধার বিশিষ্ট টিনের পাতের একটি সুস্পষ্ট (sharp) ছায়া পাওয়া উচিৎ। কিন্তু ছায়াটিকে খুব সুক্ষ্ম ভাবে লক্ষ্য করলে দেখা যাবে যে ছায়াটির ধারগুলো সুস্পষ্ট নয়। এই ঘটনা থেকে আমরা এই সিদ্ধান্ত্ে পৌছাতে পারি যে, তীক্ষ্ণ ধার বিশিষ্ট টিনের পাতের ধার ঘেঁষে যাবার সময় আলোক রশ্মি বেঁকে যায়। পরীক্ষায় দেখা গেছে কোনো প্রতিবন্ধকের ধার ঘেঁষে অথবা কোনো সূক্ষ্ম ছিদ্র বা চিড়ের মধ্য দিয়ে যাবার সময় যেকোনো তরঙ্গের গতিমুখ পরিবর্তিত হয়। একে তরঙ্গের অপবর্তন বলে। আলো তরঙ্গধর্মী হওয়ায় আলোরও অপবর্তন ঘটে।
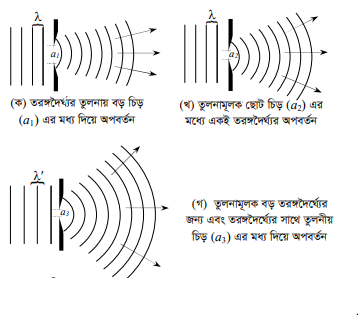
অপবর্তনঃ
আলোক রশ্মির সম্মুখে কোনো তীক্ষ্ণ ধার বিশিষ্ট অস্বচ্ছ বস্তু থাকলে বা কোনো সুক্ষ্ম চির বা ছিদ্র থাকলে বাধা বা ছিদ্রের ধার ঘেঁষে বাঁক ঘুরে জ্যামিতিক ছায়ার মধ্যে আলোর অনুপ্রবেশ ঘটে। বাঁক ঘুরে জ্যামিতিক ছায়া অঞ্চলে আলোর অনুপ্রবেশের ঘটনাকে আলোর অপবর্তন বলে।
অপবর্তনের শর্তঃ
১। তীক্ষ্ণ ধারের ক্ষেত্রে ধার খুব তীক্ষ্ণ হতে হবে যেন এর বেধ বা প্রস্থ আলোর তরঙ্গ দৈর্ঘ্যের সাথে তুলনীয় হয়। ২। সূক্ষ্ম চিড়ের ক্ষেত্র চিড়ের বেধ খুব সুক্ষ্ম হতে হবে যেন এর বেধ বা প্রস্থ আলোর তরঙ্গ দৈর্ঘ্যের সাথে তুলনীয় হয় এবং ছিদ্রের ক্ষেত্রে ছিদ্র খুব ক্ষুদ্র হতে হবে যেন এর বেধ আলোর তরঙ্গ দৈর্ঘ্যের সাথে তুলনীয় হয়।
ব্যতিচার ও অপবর্তনের মধ্যে তুলনা (Comparison between Interference and Diffraction of Light):
(ক) সাদৃশ্য:
আলোর ব্যতিচার ও অপবর্তন উভয় ঘটনাই আলোকতরঙ্গের উপরিপাতনের ঘটনা। অপবর্তনে ঝালর গঠনের কারণ হলো ব্যাতিচার ।
(খ) বৈসাদৃশ্য:
সাধারণ ব্যাতিচারের সঙ্গে অপবর্তনের কিছু পার্থক্য আছে। ব্যতিচার ও অপবর্তনের মধ্যে পার্থক্য নিম্নে দেয়া হলো ।
ব্যতিচার | অপবর্তন |
| ১। একই বিড়ার ও একই তরঙ্গদৈর্ঘ্যের দুটি আলোক উৎস থেকে একই দশা পার্থক্যের দুটি তরঙ্গ নির্গত হয়ে উপরিপাতনের ফলে লব্ধি আলোক তরঙ্গে কোথাও উজ্জ্বল এবং কোথাও অন্ধকারের সৃষ্টি হয় একে ব্যতিচার বলে । | ১। একটি তরঙ্গমুখের বিভিন্ন অংশের গৌণ আলোক উৎস থেকে অনুতরঙ্গ নির্গত হয়ে উপরিপাতনের ফলে লব্ধি আলোক তরঙ্গে কোথাও উজ্জ্বল এবং কোথাও অন্ধকারের সৃষ্টি হয়। একে অপবর্তন বলে। |
| ২। ব্যতিচার সজ্জার উজ্জ্বল ও অন্ধকার পট্টিগুলোর বেধ সমান থাকে। | ২। অপবর্তন সজ্জার পট্টিগুলোর বেধ কখনো সমান থাকে না । |
| ৩। ব্যতিচার সজ্জার অন্ধকার পট্টিতে কোনো আলো থাকে না । | ৩। অপবর্তন সজ্জার অন্ধকার পট্টিতে কিছু আলো থাকে এবং পট্টির ক্রম যত বেশী হয় আলোর পরিমাণ তত বাড়তে থাকে। |
| ৪। ব্যতিচার সজ্জার উজ্জ্বল পট্টিগুলোর আলোক প্রাবল্য সমান থাকে । | ৪। অপবর্তন সজ্জার ক্ষেত্রে কেন্দ্রীয় উজ্জ্বল পট্টির উজ্জ্বলতা সর্বাধিক। পরবর্তী উজ্জ্বল পট্টিগুলোর উজ্জ্বলতা ক্রমশ কমতে থাকে । |
অপবর্তনের প্রকার (Type of Diffraction):
অপবর্তন দুই প্রকার, যথা: ক) ফ্রনহপার শ্রেণী অপবর্তন এবং (খ) ফ্রেনেল শ্রেণী অপবর্তন। ফ্রনহফার শ্রেণী অপবর্তনঃ যে সব অপবর্তনের ক্ষেত্রে প্রতিবন্ধক বা চিড় বা ছিদ্র থেকে আলোক উৎস এবং পর্দা উভয়ই কার্যকরভাবে অসীম দূরত্বে থাকে তাদেরকে ফ্রনহফার শ্রেণী অপবর্তন বলে। এক্ষেত্রে আপতিত তরঙ্গমুখ সমতল হয়।
ফ্রেনেল শ্রেণী অপবর্তনঃ
যে সব অপবর্তনের ক্ষেত্রে প্রতিবন্ধক বা চিড় বা ছিদ্র থেকে আলোক উৎস এবং পর্দা উভয়ই কার্যকরভাবে সসীম দূরত্বে থাকে তাদেরকে ফ্রেনেল শ্রেণী অপবর্তন বলে। এক্ষেত্রে আপতিত তরঙ্গমুখ গোলীয় বা চোঙ আকৃতির হয় ।
একক চিড়ের জন্য ফ্রনহফার অপবর্তন (Fraunhofer Diffraction by Single Slit):
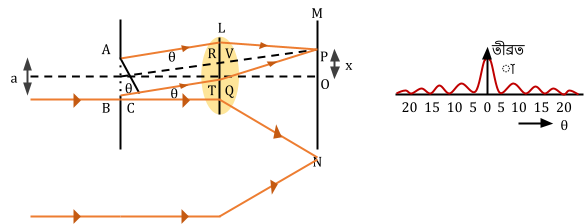
ফ্রনহফার একক চিড় অপবর্তনের জন্য a প্রস্থের অতি ক্ষুত্র একটি চিড় AB (চিত্রে অনেক বড় করে দেখানো হয়েছে) এর সম্মুখে L। লেন্স রেখে লেন্সের অপরদিকে তার ফোকাসে একবর্ণী আলোক উৎস S স্থাপন করা হয়। ফলে MN সমতল তরঙ্গমুখ বিশিষ্ট প্রতিসৃত সমাাল একবর্ণী আলোক রশ্মি পাওয়া যাবে। এই সমাড় রাল একবর্ণী আলোক রশ্মি AB চিড়ের মধ্য দিয়ে L2 লেন্সে আপতিত হয় এবং সবশেষে L2 লেন্স দ্বারা প্রতিসরিত হয়ে L2 এর ফোকাস তলে ও কাগজ তলের সাথে লম্ব OP পর্দার উপর আপতিত হয়।
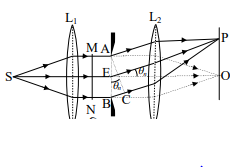
SO রেখা OP পর্দার উপর লম্ব এবং AB চিড়ের এর মধ্য বিন্দু E গামী। চিড় NB AB এর তলে সমতল তরঙ্গমুখের প্রতিটি বিন্দু হাইগেসের নীতি অনুসারে গৌণ উৎস হিসাবে ক্রিয়া করে সবদিকে অণুতরঙ্গ ছড়িয়ে পড়ে। সুতরাং AB চিড় থেকে অপবর্তিত অণুতরঙ্গগুলো সমাাল রশ্মির গোষ্ঠী সৃষ্টি করে সমদশায় চলতে শুর— করবে। যে সব সমাাল অণুতরঙ্গগুলো আপতিত রশ্মির সমাাল সেগুলোর পথপার্থক্য না থাকায় সকলেই সমদশায় L দিয়ে প্রতিসৃত হয়ে O বিন্দুতে মিলিত হবে এবং তীব্রতা সর্বোচ্চ হবে। একে কেন্দ্রীয় চরম (central maxima) বিন্দু বলে।
যে সব সমাাল উপতরঙ্গগুলো ৪ কোণে অপবর্তিত হবে সেগুলোর পথপার্থক্য থাকায় সকলেই ভিন্ন সমদশায় L2 দিয়ে প্রতিসৃত হয়ে P বিন্দুতে মিলিত হবে। এদের তীব্রতা নির্ভর করবে সমাাল অণুতরঙ্গগুলোর পথ পার্থক্যের উপর।
8n কোণে অপবর্তিত সমারাল অণুতরঙ্গগুলো সমতল তরঙ্গমুখ AC ।
সুতরাং A ও B বিন্দুর সমারাল অণুতরঙ্গ দুটির পথ পার্থক্য BC।
চিত্রানুসারে, BC = a sin8n
কিন্তু ৪n কোণে অপবর্তিত সমাাল অণুতরঙ্গগুলোর সকলের পথপার্থক্য সমান নয়।
চিরের মধ্যবিন্দু E তে পথপার্থক্য BC/2 = a/2sin8
এখন চিড়ের মধ্যে a/2 দূরত্বের অসংখ্য জোড়া জোড়া বিন্দু বিবেচনা করা যায় যাদের পথপার্থক্য সমান।
আমরা ব্যতিচারের ধর্ম থেকে পাই, যদি পথপার্থক্য λ এর পূর্ণ গুণিতক হয় তবে চরম (উজ্জ্বল) এবং যদি পথপার্থক্য
λ/2 এর বিজোড় গুণিতক হয় তবে অবম (অন্ধকার) ব্যতিচার সৃষ্টি করে।
যখন n=1 তখন 8 = 81 অর্থাৎ প্রথম ক্রম। এই অবস্থায় AP ও CP এর মধ্যে পথপার্থক্য BC = λ, ফলে এই দুটি λ অনুতরঙ্গের উপরিপাতলের ফলে পর্দা উজ্জ্বল হবে। কিন্তু AP ও EP কিংবা EP ও CP এর মধ্যে পথপার্থক্য λ/2। এছাড়া AC চিড়ের মধ্যে AE কংবা EC এর সমান অসংখ্য জোড়া জোড়া বিন্দু আছে যাদের অণুতরঙ্গের মধ্যে পথপার্থক্য λ/2। এদের সকল জোড়ার উপরিপাতনের ফলে পর্দার একই বিন্দুতে অন্ধকার হবে। ফলে সামগ্রিক ভাবে ঐ স্থানে অন্ধকার থাকবে।
সুতরাং, n = 1 হলে প্রথম অবম (অন্ধকার) বিন্দু সৃষ্টি হবে।
অতএব, a/2sin81 = λ/2
বা, asin8 = λ
এখন যদি পথপার্থক্য BC = nλ হয় তবে 8 = 8n হবে। সেক্ষেত্রে n তম অবম (অন্ধকার) বিন্দু পাওয়া যাবে।
সুতরাং / তম অবম (অন্ধকার) বিন্দু গঠনের জন্য,
a sin8n = nλ ……………………(19)
একইভাবে যদি পথ পার্থক্য BC = (2n+1)/2λ তবে একই কারণে চরম (উজ্জ্বল) বিন্দু সংঘটিত হবে।
সুতরাং n তম চরম (উজ্জ্বল) বিন্দু গঠনের জন্য,
a sin8n = (2n+1)/2λ ……………………(20)
আমরা আগেই আলোচনা করেছি যে অপবর্তন পেতে হলে চিড়ের প্রস্থ আলোর তরঙ্গদৈর্ঘ্যর সাথে তুলনীয় হতে হবে।
উদাহরণস্বরূপ ধরা যাক, সোডিয়াম বাতি থেকে নির্গত হলুদ একবর্ণী আলোর তরঙ্গদৈর্ঘ্য 5890Å = 5890 x 10-10 m = 5.89×107m এবং পরীক্ষণের জন্য যে চিড় ব্যবহার করা হয় তার প্রস্থ 0.2 mm = 2×10-4 m তাহলে প্রথম ক্রম অন্ধকার বিন্দু পেতে হলে যে কৌণিক সরণ লাগবে তা হলো 2×10-4 sin8n = 5.89 x 10-7
বা, sin8n = 5.89×10-7 /2×10-4 = 2.45×10-3
বা, 8n = 5.89×10-7/ 2×10-4 = sin-12.45×10-3 = 0.17°
এখান থেকে সহজেই বোঝা যায় যে কোণের মান খুব ক্ষুদ্র হয়। সেক্ষেত্রে আমরা লিখতে পারি sin 0 ≈ 0 । তাহলে আমরা 18 নং সমীকরণকে লিখতে পারি,
8n = nλ /a ……………………(21)
কেন্দ্রীয় চরম বিন্দু O থেকে n তম অবম বিন্দুর দূরত্ব OP = x, এবং চিড় থেকে পর্দার দূরত্ব _ OE = D হলে,
tan8n = 8n = xn/D
সুতরাং, xn/D = nλ/a
বা, x = nλD/a
(9.08) ……………………(22)
(22 নং) সমীকরণের সাহায্যে কেন্দ্রীয় চরম বিন্দু থেকে n তম অবম বিন্দুর দূরত্ব নির্ণয় করা যায়।
আবার কেন্দ্রীয় চরম বিন্দু উভয় পার্শ্বে প্রথম অবম বিন্দুদ্বয়ের মধ্যে কৌণিক দূরত্বকে কেন্দ্রীয় চরম বিন্দুর কৌণিক বেধ বলে ।
(21 নং) সমীকরণে n = 1 বসালে কেন্দ্রীয় চরম বিন্দুর প্রতি পার্শ্বে কৌণিক বেধ পাওয়া যাবে কারণ n = 1 বসালে প্রথম অবম বিন্দু পাওয়া যায় ।
সুতরাং, (৭.৩৩ নং) সমীকরণে n = 1 বসালে, 8 = λ/a
তাহলে, কেন্দ্রীয় চরম বিন্দুর কৌণিক বেধ,
28= 2λ/a ……………………(23)
ফ্রনহফার একচিড় অপবর্তনের ক্ষেত্রে কেন্দ্রীয় চরম বিন্দুর দুই দিকে প্রথম অবম বিন্দুর কৌণিক অবস্থান sin 6 = 1 a
সুতরাং, নির্দিষ্ট তরঙ্গদৈর্ঘ্যের আলোক রশ্মির জন্য প্রথম অবম বিন্দুর কৌণিক অবস্থান চিড়ের প্রস্থের সমানুপতিক। তাই চিড়ের বেধ a যত ছোট হবে ৪ মান তত বৃদ্ধি পাবে ফলে কেন্দ্রীয় চরম বিন্দু তত ছোট হবে।
যখন 0 = 90° তথন sin 90 = λ /a = 1
বা, a = λ
অর্থাৎ, যদি a = λ হয় তবে 8 = 90°, ফলে সমগ্র পর্দা কেন্দ্রীয় চরম বিন্দু দখল করে নিবে।
আলোর সমবর্তন (Polarisition of Light):
আলোর ব্যতিচার ও অপবর্তন থেকে প্রমাণিত হয় যে, আলোক তরঙ্গ আকারে সঞ্চালিত হয়। কিন্তু এই তরঙ্গ তির্যক না লম্বিক সেটি এই ঘটনাগুলো থেকে বোঝা সম্ভব নয়। আলোর সমবর্তন বা পোলারায়নের ঘটনা নিশ্চিৎ ভাবে প্রমাণ করে যে আলোক তরঙ্গ হলো এক প্রকার তির্যক তরঙ্গ। এটি লম্বিক তরঙ্গ নয়, কারণ লম্বিক তরঙ্গের সমবর্তন সম্ভব নয়। আলোর সমবর্তন সম্পর্কে আলোচনার আগে তির্যক তরঙ্গের সমবর্তন ও সমবর্তিত তরঙ্গ সম্পর্কে জানা প্রয়োজন ।
আলো কোন মাধ্যমের মধ্য দিয়ে গমনের পর আলোক তরঙ্গের কম্পন একটি নির্দিষ্ট দিকে বা তলে হওয়ার ঘটনাকে বলা হয় আলোর সমবর্তন। কোনো আলোক রশ্মির কম্পন কেবল মাত্র একটি নির্দিষ্ট দিকে বা তলে হলে ঐ আলোকে বলা হবে সমবর্তিত।
নিচে তির্যক তরঙ্গের সমবর্তন ব্যাখা করা হলো।
যান্ত্রিক তরঙ্গের সমবর্তন (Polarisition of Mechanical Wave):
দুটি কার্ড বোর্ডের মাঝখানে পাতলা ফালি করে কেটে C ও C2 চিড় তৈরি করা হলো। লম্বা দড়ি OE -কে একটি দৃঢ় অবলম্বন E সাথে বেঁধে C ও C, চিড়ের ভিতর দিয়ে পার করে দড়ির অপর প্রার্ল্ড O-কে ধরে টেনে অনুভূমিক করে রাখা হলো। এবার দড়ির অপর প্রার্ল্ড O-কে ধরে OE -এর সঙ্গে লম্বভাবে কাঁপানো হলো। এর ফলে একটি তির্যক তরঙ্গ দড়ি বরাবর OE -এর দিকে অগ্রসর হবে (চিত্র ৭.১৩-এর ক ও খ)।
তির্যক তরঙ্গটি OE বরাবর X – অক্ষের দিকে অগ্রসর হচ্ছে ধরা হলে দড়ির কণাগুলোর কম্পন হবে X – অক্ষের সাথে লম্বভাবে অর্থাৎ YZ – সমতল বরাবর। দড়ির o প্রাড় ধরে এলোমেলো ভাবে অর্থাৎ YZ – সমতলের যেকোনো দিকে বরাবর কাঁপানো যেতে পারে। তাহলে O থেকে C এর মধ্যবর্তী অংশে অবস্থিত দড়ির কণাগুলোর প্রতিটি তির্যক কম্পন জনিত বেগের Y ও Z – অক্ষ বরাবর দুটি লম্ব উপাংশ থাকবে ।
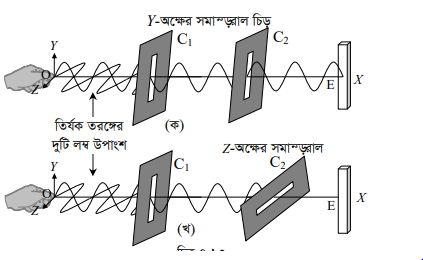
C1 চিড়টি Y -অক্ষের সমান্দ্রালে রাখা আছে। ফলে C চিড়টি এই কম্পনের Z -অক্ষ বরাবর কম্পনকে বাধাগ্রস্থ করবে। ফলে শুধু Y – অক্ষের সমাাল উপাংশটি বিনা বাধায় এই চিড় দিয়ে সঞ্চালিত হবে। সুতরাং OC, অংশে দড়ির কম্পন যতই এলোমেলো হোক না কেন CC, অংশে দড়িটি শুধু Y -অক্ষ বরাবরই কম্পিত হবে। এলোমেলো কম্পনযুক্ত তির্যক কম্পনকে একটি নির্দিষ্ট অক্ষ বরাবর সীমাবদ্ধ করার ঘটনাকে সমবর্তন বলে। তাহলে বলা যায় OC, অংশে দড়ির কম্পন অসমবর্তিত এবং C, চিড়টি দিয়ে অতিক্রম করার পর C,C, অংশে দড়ির কম্পন সমবর্তিত।
আবার যেহেতু ৭.১৩ -এর ক নং চিত্রে C, চিড়টিও Y -অক্ষের সমান্ত্ রাল এবং CC, অংশে দড়িটি শুধু Y -অক্ষ বরাবরই কম্পিত হচ্ছে সেহেতু এই তরঙ্গ বিনা বাঁধায় C, চিড় অতিক্রম করে E পর্যড্ বিার লাভ করবে। তাই C E অংশের দড়িটিও শুধু Y -অক্ষ বরাবরই কম্পিত হবে। ৭.১৩ -এর খ নং চিত্রে C, চিড়টিও Z -অক্ষের সমাাল এবং CC, অংশে দড়িটি শুধু Y -অক্ষ বরাবরই কম্পিত হচ্ছে সেহেতু এই তরঙ্গকে C, চিড় অতিক্রম করতে বাঁধা দিবে ফলে C, চিড় এই তরঙ্গ অতিক্রম করতে পারবে না। তাই C,E অংশের দড়িটিতে কোনো তরঙ্গ থাকবে না। এর থেকে এটিও প্রমাণিত হয় যে, তারে যদি লম্বিক তরঙ্গ হতো Y (খ)
অর্থাৎ এর কম্পন যদি X – অক্ষের সমাাল তাহলে C ও C, চিড় দুটি যে অক্ষ বরাবরই থাকুক না কেন তরঙ্গ ( থেকে E পর্যড্ বিস্তৃর লাভ করতো। কোনো চিড়ই একে বাঁধা দান করতো না। তাহলে বলা যায় যে, লম্বিক তরঙ্গের কোনো সমবর্তন হয় না। তাই শব্দ তরঙ্গের সমবর্তন হয় না।
টুরম্যালিন কেলাসের পরীক্ষা (Experiment with Tourmaline Crystal) :
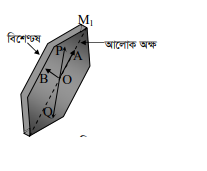
টুরম্যালিন এক ধরণের ষড়ভুজাকৃতির কেলাস বা স্ফটিক (tourmaline crystal)। পাতলা পাতের আকারে কাটা কেলাসটি প্রায় স্বচ্ছ পদার্থের ন্যায় আচরণ করে। ষড়ভুজের বৃহত্তম কর্ণটিকে কেলাসের আলোক-অক্ষ (Optical Axis) বলে। চিত্র নং ৭.১৪ ক-তে CT ও C দুটি টুরম্যালিন কেলাসের পাতলা পাত এবং যথাক্রমে M,M¥ ও M2M এদের আলোক-অক্ষ ।
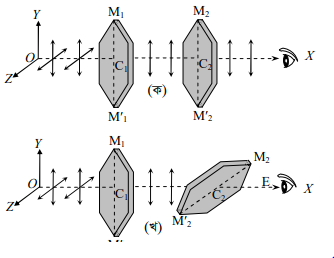
M₁ ধরা যাক, কোনো উৎস O থেকে X – অক্ষ বরাবর আলো টুরম্যালিন কেলাস C, এর উপর আপতিত হচ্ছে। C কেলাসটি এমন ভাবে অবস্থিত যেন এর আলোক- অক্ষ M M¥ টি X -অক্ষের সাথে লম্ব থাকে। উৎস থেকে আলোকরশ্মি C, কেলাস অতিক্রম করে চোখে এসে পৌছালে কেলাসের কারণে আলোর উজ্জ্বলতা খানিকটা হ্রাস পায়। এই অবস্থায় OX রশ্মির সাপেক্ষে C কেলাসটিকে ঘোরালে উজ্জ্বলতার আর কোনো পরিবর্তন হবে না।
এবার C, কেলাসটিকে OX রশ্মির পথের উপর এমন ভাবে বসানো হলো যেন এর আলোক-অক্ষ M2M2 টি M,M আলোক-অক্ষের সমাালে থাকে (চিত্র নং ৭.১৪ ক)। এই অবস্থায় পূর্বে যে পরিমান উজ্জ্বলতা চেখে এসে পড়ছিল এখনো তাই পড়বে ।
এখন C, কেলাসটিকে স্থির রেখে C, কেলাসটিকে ধীরে ধীরে ঘোরানো হলো। দেখা যাবে আলোর উজ্জ্বলতা ক্রমশ হ্রাস পাচ্ছে এবং C2 কেলাসটিকে যখন আলোক-অক্ষের সাথে 90° কোণ করে অর্থাৎ Y -অক্ষ বরাবর অবস্থান করে তখন উৎস থেকে কোনো আলো চোখে পড়ে না (চিত্র নং ৭.১৪ খ)। C, কেলাসটিকে আরো ঘোরালে আবার উজ্জ্বলতা বাড়তে থাকে এবং 180° কোণে আসলে আবার উজ্জ্বলতা ফিরে পায় (চিত্র নং ৭.১৪ ক) ।
এ পরীক্ষা থেকে দেখা যায়, আলো লম্বিক তরঙ্গাকারে সঞ্চালিত হয় না। আলো যদি লম্বিক তরঙ্গাকারে সঞ্চালিত হতো, তবে C, কেলাসটিকে ঘুরানোর ফলে আলোর উজ্জ্বলতার কোনো পরিবর্তন হতো না। আলোতরঙ্গকে তির্যক তরঙ্গ হিসাবে ধরে নিলে এবং টুরম্যালিন কেলাসে আলোক অক্ষকে সর- চিড় হিসাবে বিবেচনা করলে উপরের পরীক্ষাটির ব্যাখ্যা পাওয়া যায়। O উৎসের আলোক তরঙ্গের তির্যক কম্পনগুলো এলোমেলো প্রকৃতির।
সুতরাং আলোর OC অংশের প্রতিটি বিন্দুতে Y ও Z – অক্ষ বরাবর কম্পনে দুটি লম্ব উপাংশ থাকে। যেহেতু C, কেলাসের MM আলোক-অক্ষটি Y -অক্ষের সমাাল থাকায় আলোকরশ্মির Y -অক্ষ বরাবর তির্যক কম্পনের উপাংশ বিনা বাঁধায় অতিক্রম করছে কিন্তু Z -অক্ষ বরাবর তির্যক কম্পনের উপাংশ বাঁধা প্রাপ্ত হয়েছে।
যেহেতু Z -অক্ষ বরাবর তির্যক কম্পনের উপাংশ সম্পূর্ণরূপে শোষিত হয়েছে সেহেতু আলো উজ্জ্বলতা অর্ধেক হয়ে যাবে। আবার যতক্ষণ C, কেলাসটিকে আলোক-অক্ষটি Y -অক্ষের সমাাল ছিল ততক্ষণ C থেকে C, কেলাসের মধ্যে থাকা Y -অক্ষ বরাবর তির্যক কম্পন বিনা বাঁধায় অতিক্রম করেছে। তাই অপর পারে চোখে আলো পৌছিয়েছে।
যখন C, কেলাসের M2M’ আলোক-অক্ষটি 90° কোণ ঘুরিয়ে Z -অক্ষ বরাবর করা হলো তখন C থেকে C, কেলাসের মধ্যে থাকা Y -অক্ষ বরাবর তির্যক কম্পনের উপাংশ বাঁধা প্রাপ্ত হবে ফলে কোনো কম্পন অর্থাৎ আলো দেখা যাবে না। C2 কেলাসকে আরো 90° কোণ ঘুরিয়ে 180° কোণে আনলে C, কেলাসের M2M2 আলোক-অক্ষটি আবার Y -অক্ষ বরাবর হয়ে যাবে ফলে উজ্জ্বলতার পূর্বের ন্যায় ফিরে আসবে। এর থেকে এই সিদ্ধার্ল্ডে উপনিত হওয়া যায় যে,
১। যখন কোনো আলোকরশ্মি বা আলোকতরঙ্গ কোনো টুরম্যালিন কেলাসের মধ্য দিয়ে গমন করে তখন এর এলোমেলো তির্যক তরঙ্গ একটি একমুখী তির্যক তরঙ্গে রূপান্ডুরিত হয়। এই ঘটনাকে আলোর সমবর্তন বলে এবং ঐ আলোকে সমবর্তিত আলো বলে ।
২। আলোর মত যেকোনো তির্যক তরঙ্গেরই সমবর্তন হয়।
৩। যার সাহায্যে আলোর সমবর্তন ঘটানো হয় তাকে বলা হয় সমবর্তক বা পোলারাইজার (Polarizer) বলে। (৭.১৪) চিত্রে C হলো সমবর্তক এবং এর M,M আলোক অক্ষটি হলো তার সমবর্তক অক্ষ ।
যার সাহায্যে কোনো আলো সমবর্তিত কি না তা নির্ধারণ করা হয় তাকে বলা হয় বিশেষক বা এ্যানালাইজার (analyser)। (৭.১৪) চিত্রে C2 হলো বিশেষক কারণ, এই কেলাস দিয়ে আলো সমবর্তিত কি না এবং C কেলাস দিয়ে কী ধরণের সমবর্তন ঘটলো তা বিশেষণ করা যায়। C ও C, কেলাস দুটির আলোক অক্ষ সমাাল হলে সমবর্তক এবং বিশেষকের অবস্থানকে সমাাল অবস্থান বলা হয় এবং কেলাস দুটির আলোক অক্ষ পরস্পর লম্ব হলে সমবর্তক এবং বিশে ষকের অবস্থানকে আড়াআড়ি অবস্থান বলা হয়।
ম্যালাসের সূত্র (Malus Law)
যখন কোন অসমবর্তিত আলো পর পর দুটি সমবর্তকের (একটি সমবর্তক ও অপরটি বিশেষক) মধ্য দিয়ে গমন করে তখন নির্গত আলোর তীব্রতা সমবর্তকদ্বয়ের নিঃসরণ তলের মধ্যবর্তী কোণের উপর নির্ভর করে। ম্যালাস এর তীব্রতা সংক্রাড় একটি সূত্র প্রদান করেন। সূত্রটি ম্যালাসের সূত্র নামে পরিচিত। সূত্রটি হলো, “সমবর্তিত আলো বিশেষকের মধ্য দিয়ে গমনের ফলে এর তীব্রতা সমবর্তক ও বিশেশ্চষকের নিঃসরণ তলের মধ্যবর্তী কোণের cosine-এর সমানুপাতিক” ।
সূত্রের প্রমাণ :
ধরা যাক, একটি আলোক রশ্মি সমবর্তকের মধ্য দিয়ে অতিক্রম করে সমতল সমবর্তিত হলো। এই সমবর্তিত আলোক রশ্মির কম্পন তল সমবর্তকের আলোক অক্ষের PQ এর সমাাল। এই রশ্মি পরবর্তিতে বিশেষক অতিক্রম করে নির্গত হলো। এই কম্পন বিার OP = a । বিশেষকের আলোক অক্ষ M,M¥ টি সমবর্তিত আলোর কম্পন তলের সাথে ৪ কোণে হেলানো (চিত্র ৭.১৫)। আমরা জানি, প্রাবল্য বিারের বর্গের সমানুপাতিক।
সুতরাং, আপতিত আলোর তীব্রতা Io = ka2 । এখানে, k একটি ধ্রুবক। OP ও বিশেষকের আলোক অক্ষের মধ্যবর্তী কোণ 6। যেহেতু সমবর্তকের আলোক অক্ষ PQ-এর সমারাল সেহেতু সমবর্তক ও বিশেষকের নিঃসরণ তলের মধ্যবর্তী কোণ । OP দুটি লম্ব উপাংশে বিভক্ত করা হলো। একটি বিশেষকের নিঃসরণ তলের সমাাল OA = acose এবং অপরটি OA-এর সমকোণে OB = asin 6 । শুধুমাত্র OA = acose উপাংশ বিশেষকের মধ্য দিয়ে অতিক্রম করবে অর্থাৎ, নির্গত আলোর কম্পনের বিড়ার হবে acose । সুতরাং, বিশেষক থেকে নির্গত আলোর তীব্রতা,
I = ka² cos²8
বা, I = Io cos28 ……………………(24)
এটিই ম্যালাসের সূত্র।
যখন 8 = 0° , অর্থাৎ সমবর্তক ও বিশেষকের নিঃসরণ তল সমাাল তখন, I = Io, (যেহেতু, cos 0 ° =1)
আবার, যখন 8 = 90° অর্থাৎ সমবর্তক ও বিশেষকের নিঃসরণ তল পরস্পর লম্ব তখন, I = 0 (যেহেতু, cos90 = 1 )
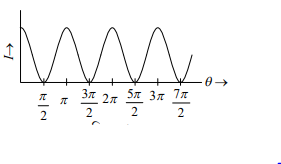
সমবর্তক ও বিশেষকের নিঃসরণ তলের মধ্যবর্তী কোণের সাথে নির্গত আলোর তীব্রতার পরিবর্তন (৭.১৬ নং) চিত্রের সাহায্যে দেখা হলো ।
অসমবর্তিত আলো (Unpolarised Light)
সূর্যের আলো, বৈদ্যুতিক বাতির আলো, মোমবাতির আলো ইত্যাদি প্রচলিত আলো উৎসের মধ্যে ইলেকট্রন, আয়ন বা চার্জিত কণাগুলো সম্পূর্ণ রূপে বিক্ষিপ্ত ভাবে কম্পিত হতে থাকে। ফলে এই সব উৎস থেকে নির্গত আলোক রশ্মি নির্দিষ্ট দিকে গমন করলেও এদের সৃষ্ট তির্যক কম্পন কোনো নির্দিষ্ট দিকে থাকে না। এই ধরণের আলোকে সাধারণ আলো বা অসমবর্তিত আলো বলে। এই ক্ষেত্রে তির্যক কম্পনকে দুটি সমান বিার যুক্ত লম্ব উপাংশের সমষ্টি হিসাবে নির্দেশ করা যায়।
সাধারণ আলো হলো একপ্রকার তাড়িতচৌম্বক তরঙ্গ। এই ধরণের তরঙ্গের তড়িৎ ক্ষেত্র É এবং চৌম্বক ক্ষেত্র B তরঙ্গের গতির অভিমুখের সঙ্গে সব সময় পরস্পর লম্বভাবে কম্পিত হয়। এই কম্পনটি একটি নির্দিষ্ট তলে সীমাবদ্ধ থাকে। আলো নামক তাড়িতচৌম্বক তরঙ্গটি এই তলের সাথে লম্ব অভিমুখে সঞ্চালিত হয়।
সুতরাং, বলা যায়, আলোর গতি পথের সমকোণে অর্থাৎ লম্বভাবে অবস্থিত কোনো নির্দিষ্ট তলের উপর একটি বিশেষ অক্ষ বরাবর হওয়ার ঘটনাকে আলোর সমবর্তন বলে।
অসমবর্তিত এবং সমবর্তিত আলোকরশ্মির অঙ্কণের প্রথা (Convention of Representation of Unpolarised and Polarised Light) :
কাগজের তলে অসমবর্তিত এবং সমবর্তিত আলোকরশ্মি নীচে লিখিত প্রথা অনুযায়ী অঙ্কন করা হয় ।
১। অসমবর্তিত আলোকরশ্মি তরঙ্গের কম্পন তরঙ্গ সঞ্চালনের অভিমুখের সাথে অভিলম্ব তলে সব দিকে ঘটে (চিত্র ক) । সেজন্য একে পারস্পরিক অভিলম্ব দিকে দুটি স্পন্দনের সমষ্টি হিসাবে গণ্য করা হয়। সেজন্য অসমবর্তিত আলোকরশ্মি অঙ্কনের ক্ষেত্রে ডট (.) এবং বিপরীতমুখী তীরচিহ্ন (I) সহ ভাঙ্গা ভাঙ্গা রেখা দিয়ে সংযুক্ত ব্যবহার করা হয় (চিত্র খ)।
২। সমবর্তিত আলোকরশ্মি তরঙ্গের কম্পন কাগজ তলে সম্পন্ন হলে এই কম্পন্ন গতির অভিমুখে অভিলম্ব তলে বিপরীতমুখী তীরচিহ্ন (1) সহ ভাঙ্গা ভাঙ্গা রেখা দিয়ে সংযুক্ত ব্যবহার করা হয় (চিত্র গ) ।
৩। সমবর্তিত আলোকরশ্মি তরঙ্গের কম্পন কাগজ তলের সাথে অভিলম্ব বরাবর সম্পন্ন হলে এই কম্পন্ন গতির অভিমুখে বরাবর কতকগুলি ডট (.) সহ ভাঙ্গা ভাঙ্গা রেখা দিয়ে সংযুক্ত ব্যবহার করা হয় (চিত্র ঘ)।

কম্পন তল ও সমবর্তন তল (Plane of Vibration abd Plane of Polarisition):
কম্পন তল:
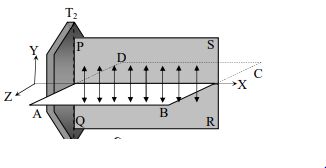
সমবর্তিত আলোর কম্পন যে তলে অবস্থান করে বা সীমাবদ্ধ থাকে সেই তলকে কম্পন তল বলে চিত্রে T T টুরম্যালিন কেলাসের মধ্য দিয়ে নির্গত সমবর্তিত আলোকরশ্মি দেখানো হলো। আলোকরশ্মি X – অক্ষ বারাবর সঞ্চালিত হচ্ছে এবং সমবর্তিত আলোকরশ্মির বিন্দুগুলো Y -অক্ষ বরাবর কম্পিত হচ্ছে। তাহলে চিত্রে XY তলটি অর্থাৎ যে তলে আলোকরশ্মির বিন্দুগুলো কম্পিত হচ্ছে সেই PQRS তলটি হলো কম্পন তল ।
সমবর্তন তল:
কম্পন তলের সাথে লম্বভাবে অবস্থিত তলের উপরে আলোকরশ্মিটি বর্তমান, সেই তলটিকে সমবর্তন তল বলে।
চিত্রে T,T, টুরম্যালিন কেলাসের মধ্য দিয়ে নির্গত সমবর্তিত আলোকরশ্মির ABCD তলের উপর লম্বভাবে কম্পন তলটি অবস্থিত এবং এই তলে আলোকরশ্মি বিন্দুগুলোর কোনো কম্পন নাই। তাই ABCD তলই সমবর্তন তল।
সমবর্তন কোণ (Angle of Polarisation) :
১৮০৮ খ্রিষ্টাব্দে বিজ্ঞানী ম্যালাস (Malus) প্রথম আবিস্কার করেন যে প্রতিফলকের সাহায্যে সমতল সমবর্তিত আলো উৎপন্ন করা যায়। অসমবর্তিত আলো কোনো স্বচ্ছ মাধ্যম দিয়ে (যেমন পানি, কাচ ইত্যাদি) দিয়ে প্রতিফলিত হলে প্রতিফলিত রশ্মি আংশিক সমবর্তিত হয়। রশ্মি কতখানি সমবর্তিত হবে তা আপাতন কোণের উপর নির্ভর করে।
”যে বিশেষ আপাতন কোণের জন্য কোনো নির্দিষ্ট প্রতিফলক তল থেকে প্রতিফলিত রশ্মি সম্পূর্ণরূপে সমতল সমবর্তিত হয় সেই কোণকে সমবর্তন কোণ বলে । এই কোণকে ।, দিয়ে প্রকাশ করা হয়”।
ব্রউস্টারের সূত্র (Brewster’s Law) :
সমবর্তন কোণের ট্যানজেন্টের মান সংখ্যাগতভাবে প্রতিসারক মাধ্যমের প্রতিসারণাংকের সমান ।
পরীক্ষায় দেখা গেছে যে, কোনো প্রতিসারক মাধ্যমের বিভেদ তলে আপতিত অসমবর্তিত রশ্মি অভিলম্বের সাথে যে কোণে আপতিত হলে প্রতিফলিত রশ্মি এবং প্রতিসরিত রশ্মি পরস্পর লম্ব হয় সেই আপাতন কোণে প্রতিফলিত এবং প্রতিসরিত রশ্মিদ্বয় সমবর্তিত হয়। এই কোণকে সমবর্তন কোণ বা ব্র“স্টার কোণও বলে।
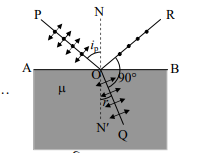
ধরা যাক, চিত্রে PO অসমবর্তিত আলোকরশ্মি AB বিভেদ তলের উপর O বিন্দুতে অঙ্কিত অভিলম্ব NON’ এর সাথে ip কোণে আপতিত হওয়ায় প্রতিফলিত রশ্মি OR এবং প্রতিসরিত রশ্মি OQ মধ্যবর্তী কোণ 90° হয়েছে। প্রতিফলনের সূত্রানুসারে, ∠PON = ∠NOR = i
এবং প্রতিসরণ কোণ ∠QON’ = r
চিত্রানুসারে, ∠NOR + ∠ROQ+∠QON’ =ip + 90° + r = 180°
বা, r = 90° –ip ……………………(25)
আবার েেলর সূত্রানুসারে, μ = sinip/ sin r = sinip/sin ( 90° – ip )= sinip/cosip
বা, tanip = μ ……………………(26)
এটিই ব্র“স্টারের সূত্র।
উদাহরণ ১ :
একটি ফ্রনহফার শ্রেণীর একক চিড়ের দরণ অপবর্তন পরীক্ষায় 5890Å তরঙ্গদৈর্ঘ্যের আলো ব্যবহার করা হল। প্রথম অবমের জন্য অপবর্তন কোণ নির্ণয় করন। চিড়ের বেধ 0.1mm
সমাধানঃ
দেয়া আছে, a = 5890A = 5890 × 10 “m, d = 0.1mm =10″m, n=1 এবং 8n = 81 = ?
আমরা জানি, d sin8n = nλ
বা, sinsin8n = nλ/d
শর্তানুসারে, sin81 = λ/d
বা, ৪1 = sin -1 λ/d
মান বসালে, 81 = sin -1 (5890×10-10)/ 10-4 = sin 5.89 ×10-3 = 0.29
উ: 0.29°
উদাহরণ২ :
যে বর্ণের আলোর জন্য পানির প্রতিসরণাঙ্ক 1.33 তার সমবর্তন কোণ নির্ণয় করন।
সমাধানঃ
দেয়া আছে, μ = 1.33 এবং ip = ?
আমরা জানি, tanip = μ
বা, ip = tan-1μ
মান বসালে, ip = tan-11.33 = 53.1°
উ: 53.1°
উদাহরণ ৩:
নির্দিষ্ট বর্ণের আলোর জন্য 1.33 প্রতিসরণাঙ্ক পানি থেকে 1.5 প্রতিসরণাঙ্কের কাচে প্রবেশ করলে বর্ণের আলোর সমবর্তন কোণ নির্ণয় করন।
সমাধানঃ
দেয়া আছে, μw = 1.33, μg = 1.5 এবং ip = ?
আমরা জানি,
wμg = tanip এবং wμg = μg/μw
অতএব, μg/μw = tanip
মান বসালে, 1.5/1.33 = tanip
বা, ip = tan -1 1.5/ 1.33 = tan-11.128 = 48.44
উ: 48.44°
সার-সংক্ষেপ :
অপবর্তনঃ
আলোক রশ্মির সম্মুখে কোনো তীক্ষ্ণ ধার বিশিষ্ট অস্বচ্ছ বস্তু থাকলে বা কোনো সূক্ষ্ম চিড় বা ছিদ্র থাকলে বাধা বা ছিদ্রের ধার ঘেঁষে বাঁক ঘুরে জ্যামিতিক ছায়ার মধ্যে আলোর অনুপ্রবেশ ঘটে। বাঁক ঘুরে জ্যামিতিক ছায়া অঞ্চলে আলোর অনুপ্রবেশের ঘটনাকে আলোর অপবর্তন বলে।
ফ্রনহফার শ্রেণী অপবর্তনঃ
যে সব অপবর্তনের ক্ষেত্রে প্রতিবন্ধক বা চিড় বা ছিদ্র থেকে আলোক উৎস এবং পর্দা উভয়ই | কার্যকরভাবে অসীম দুরত্বে থাকে তাদেরকে ফ্রনহফার শ্রেণী অপবর্তন বলে। এক্ষেত্রে আপতিত তরঙ্গমুখ সমতল হয়। ফ্রেনেল শ্রেণী অপবর্তনঃ যে সব অপবর্তনের ক্ষেত্রে প্রতিবন্ধক বা চিড় বা ছিদ্র থেকে আলোক উৎস এবং পর্দা উভয়ই কার্যকরভাবে সসীম দুরত্বে থাকে তাদেরকে ফ্রেনেল শ্রেণী অপবর্তন বলে। এক্ষেত্রে আপতিত তরঙ্গমুখ গোলীয় বা চোঙ আকৃতির হয়।
আলোর সমবর্তন:
আলো কোন মাধ্যমের মধ্য দিয়ে গমনের পর আলোক তরঙ্গের কম্পন একটি নির্দিষ্ট দিকে বা তলে হওয়ার ঘটনাকে বলা হয় আলোর সমবর্তন। কোন আলোক রশ্মির কম্পন কেবল মাত্র একটি নির্দিষ্ট দিকে বা তলে হলে ঐ আলোকে বলা হবে সমবর্তিত আলো ।
সমবর্তক বা পোলারাইজার:
যার সাহায্যে আলোর সমবর্তন ঘটানো হয় তাকে বলা হয় সমবর্তক বা পোলারাইজার। বিশেষক বা এ্যানালাইজার: যার সাহায্যে কোনো আলো সমবর্তিত কি না তা নির্দ্ধারণ করা হয় তাকে বলা হয় বিশেষক বা এ্যানালাইজার।
ম্যালাসের সূত্র:
সমবর্তিত আলো বিশেষকের মধ্য দিয়ে গমনের ফলে এর তীব্রতা সমবর্তক ও বিশেষকের নিঃসরণ তলের মধ্যবর্তী কোণের cosine-এর সমানুপাতিক ।
সমবর্তন তল:
কম্পন তলের সাথে লম্বভাবে অবস্থিত তলের উপরে আলোকরশ্মিটি বর্তমান, সেই তলটিকে সমবর্তন তল বলে ।
সমবর্তন কোণ:
যে বিশেষ আপাতন কোণের জন্য কোনো নির্দিষ্ট প্রতিফলক তল থেকে প্রতিফলিত রশ্মি সম্পূর্ণরূপে সমতল সমবর্তিত হয় সেই কোণকে সমবর্তন কোণ বলে। এই কোণকে দিয়ে প্রকাশ করা হয়।
ব্রস্টারের সূত্র:
সমবর্তন কোণের ট্যানজেন্টের মান সংখ্যাগতভাবে প্রতিসারক মাধ্যমের প্রতিসরণাংকের সমান। অর্থাৎ tanip = μ
বহুনির্বাচনী প্রশ্নঃ
১। কোনো প্রতিবন্ধকের ধার ঘেষে বা সর চিরের মধ্যে দিয়ে যাওয়ার সময় আলোর বেঁকে যাওয়ার ঘটনাকে কি বলে?
ক. প্রতিসরণ
খ. অপবর্তন
গ. সমবর্তন
ঘ. ব্যাতিচার
২। সমবর্তন ঘটে কোন তরঙ্গের ক্ষেত্রে-
ক. শব্দ তরঙ্গ
খ. অনুতরঙ্গ
গ. অনুদৈর্ঘ্য তরঙ্গ
ঘ. তির্যক তরঙ্গ
৩। আলোর কম্পনকে আলোর গতির সাথে সমকোণে একটি নির্দিষ্ট তলে সীমাবদ্ধ করার প্রক্রিয়াকে বলে-
ক. আলোর ব্যতিচার
খ. আলোর অপবর্তন
গ. আলোর সমবর্তন
ঘ. অপবর্তন প্রতিসরণ
