আজকে আমরা আলোর ব্যতিচার : ইয়ং এর দ্বি চিড় পরীক্ষা সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৭ ভৌত আলোকবিজ্ঞান এর অন্তর্ভুক্ত।

আলোর ব্যতিচার : ইয়ং এর দ্বি চিড় পরীক্ষা
উপরিপাতন নীতি (Superposition Principle) :
তরঙ্গ প্রবাহের ফলে মাধ্যমের কণাগুলো আন্দোলিত হয়। মাধ্যমের যেকোনো কণার উপর একটি তরঙ্গ এসে আপতিত হলে কণাটির স্বাভাবিক অবস্থান থেকে সরণ ঘটে। ভিন্ন ভিন্ন তরঙ্গের জন্য সরণ ভিন্ন ভিন্ন। ধরা যাক, মাধ্যমের যেকোনো কণার উপর এক যোগে একাধিক তরঙ্গ আপতিত হলো। এখন, প্রত্যেকটি তরঙ্গ পৃথক পৃথক ভাবে আপতিত হলে মাধ্যমের কণাটির স্বাভাবিক অবস্থান থেকে পৃথক পৃথক সরণ হত। যেহেতু এক যোগে একাধিক তরঙ্গ আপতিত হয়েছে সেহেতু কণাটির এই সরণগুলো সব একসাথে ঘটেছে। সুতরাং কণাটির একটি লব্ধি সরণ ঘটবে (যেহেতু সরণ একটি ভেক্টর রাশি)। অর্থাৎ কণাটির লব্ধি সরণ হলো পৃথক পৃথক সরণগুলোর ভেক্টর যোগফলের সমান। একেই উপরিপাতন নীতি বলে ।
উপরিপাতন নীতিঃ
তরঙ্গ প্রবাহের ফলে মাধ্যমের কণাগুলো আন্দোলিত হয়। কোন মাধ্যমের মধ্য দিয়ে একাধিক তরঙ্গ সঞ্চালিত হলে কোন কণা বা বিন্দুর লব্ধি-সরণ ঘটবে। এ লব্ধি-সরণ তরঙ্গগুলো কর্তৃক পৃথক পৃথক সরণের ভেক্টর যোগফলের সমান। একে তরঙ্গের উপরিপাতন নীতি বলে।
ধরা যাক, দুটি তরঙ্গ মাধ্যমের কোনো একটি কণাকে একই সাথে অতিক্রম করল। একটি তরঙ্গে দরূন কণার সরণy, এবং অপর তরঙ্গের দরূন কণার সরণ y2 । তাহলে, উপরিপাতন নীতি অনুসারে কণাটির লব্ধি সরণ, y = y + y2
সুসঙ্গত উৎস (Coherent Sources):
যদি দুটি আলোক উৎস থেকে সব সময় একই দশার বা একই দশা পার্থক্যের তরঙ্গ নির্গত হয় তবে আলোক উৎস দুটিকে সুসংগত উৎস বলে।
আমরা পরে দেখব যে, আলোক তরঙ্গে স্থায়ী ব্যাতিচার জনিত ঝালর (Intreference Fringes) পেতে হলে দুটি সুসংগত উৎসের প্রয়োজন।। প্রকৃত পক্ষে উৎস দুটি সুসংগত না হলে কোনো বিন্দুতে কোনো এক মুহূর্তে উজ্জ্বল এবং পর মুহূর্তেই অন্ধকার দেখাবে। এই পরিবর্তন এত দ্রুত ঘটে যে বাড়বে বিন্দুটি সব সময় উজ্জ্বল মনে হয়। তাই কোনো ব্যাতিচার পাওয়া যায় না।
একই ধরণের দুটি ভিন্ন আলোর উৎস কখনো সুসংগত হয় না। শুধু তাই নয়, একই উৎসের ভিন্ন দুটি অংশের আলোক রশ্মিও সুসংগত হয় না। বিভিন্ন আলোকীয় পরীক্ষায় বিভিন্ন বিজ্ঞানী বিভিন্ন ভাবে সুসংগত উৎস সৃষ্টি করেন।
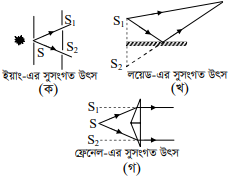
১। ইয়াং-এর দ্বি-চিড় পরীক্ষায় একটি আলোক উৎস S থেকে নির্দিষ্ট দূরত্বে রাখা দুটি চিড় S ও S, সুসংগত উৎস হিসাবে কাজ করে। (চিত্রক)
২। লয়েড-এ একক দর্পণ পরীক্ষায় একটি সর— ছিদ্র S, এবং একটি সমতল দর্পণ থেকে প্রতিফলনের ফলে সৃষ্ট S-এর একটি অবাস্তব প্রতিবিম্ব S, দর্পণের বিপরীত পৃষ্ঠে গঠিত হয়। এই S, এবং S, সুসংগত উৎস হিসাবে কাজ করে। (চিত্র খ) ৩।
ফ্রেনেল-এর যুগ্ম প্রিজম পরীক্ষায় একটি আলোক উৎস S থেকে নির্গত আলো যুগ্ম প্রিজমে আপতিত হবার পর প্রতিসরিত হয়ে দুটি অবাব প্রতিবিম্ব S, ও S, গঠন করে। এই অবাড়ব প্রতিবিম্ব S, ও S, সুসংগত উৎস হিসাবে কাজ করে। (চিত্র গ)
ব্যতিচার (Interference):
দুটি আলোক উৎস থেকে একই বিড়ারের এবং একই তরঙ্গ দৈর্ঘ্যের আলো নির্গত হয়ে কোনো বিন্দুতে আপতিত হলে উপরিপাতনের ফলে কোথাও উজ্জ্বল এবং কোথাও অন্ধকার সৃষ্টি হয়। আলোর এই উজ্জ্বলতার হ্রাস-বৃদ্ধির ঘটনাকে ব্যতিচার বলে । সমদশা সম্পন্ন আলো রশ্মির উপরিপাতনের ফলে উজ্জ্বল বা চরম এবং বিপরীত দশা সম্পন্ন আলো রশ্মির উপরিপাতনের ফলে অন্ধকার বা অবম-এর সৃষ্টি হয়। এটি একটি অবস্থানিক ঘটনা ।
ব্যতিচারের শর্তঃ-
১। উৎস দুটি সুসঙ্গত হতে হবে।
২। একই তরঙ্গদৈর্ঘ্যের আলোক উৎস হতে হবে।
৩। তরঙ্গ দুটির বিার সমান হতে হবে।
৪। তরঙ্গ উৎস দুটি খুব কাছাকাছি হতে হবে।
ইয়ং এর দ্বি চিড় পরীক্ষা (Young’s Double Slit Experiment):
L একটি একবর্ণী আলোক উৎস। এর সম্মুখে একটি সর- চিড় S-এর মধ্যদিয়ে তরঙ্গমুখ অতিক্রম করে S1 ও S2 দুটি সর— ও খুব কাছাকাছি চিড়ের মধ্য দিয়ে অতিক্রম করে। S ও S2 চিড় দুটি প্রকৃত পক্ষে সুসঙ্গত, সমতরঙ্গ দৈর্ঘ্য সম্পন্ন ও একবর্ণী আলোক উৎস হিসাবে কাজ করে। হাইগেন্সের নীতি অনুসারে Si ও S, চিড় দুটি গৌণ উৎস হিসাবে কাজ করবে এবং গৌণ উৎস দুটি হতে সৃষ্ট অনুতরঙ্গগুলো চারিদিকে ছড়িয়ে পড়ে উৎস এবং পর্দার মধ্যবর্তী অঞ্চলে অগ্রসর হবে। চিত্র-এ অবিচ্ছিন্ন বক্র রেখা দিয়ে সমদশা সম্পন্ন তরঙ্গ শীর্ষ এবং বিচ্ছিন্ন বক্র রেখা দিয়ে সমদশা সম্পন্ন তরঙ্গ পাদ দেখানো হয়েছে।
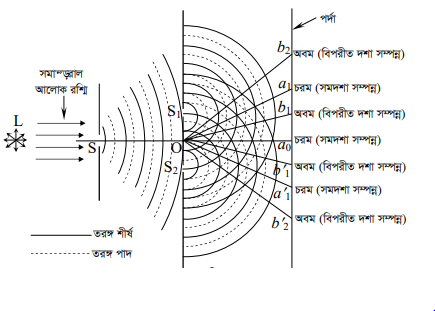
এই অনুতরঙ্গগুলোর উপরিপাতন ঘটবে। যে সব বিন্দুতে সমদশায় অনুতরঙ্গগুলোর উপরিপাতন ঘটে সে সব স্থানে উজ্জ্বল ডোরা বা চরম এবং যে সব বিন্দুতে বিপরীত দশায় অনুতরঙ্গগুলোর উপরিপাতন ঘটে সে সব স্থানে অন্ধকার ডোরা বা অবম-এর সৃষ্টি হয়। চিত্র নং (৭.৭)-তে O হলো চিড়দ্বয়ের মধ্য বিন্দু। 0 হতে পর্দা পর্যন্ত্ Oag,Oay,Oa রেখাগুলো অনুতরঙ্গের সেই সব বিন্দু দিয়ে গেছে যে সব বিন্দুতে তরঙ্গ শীর্ষ বা তরঙ্গ পাদ পরস্পরকে ছেদ করেছে। অর্থাৎ ছেদ বিন্দুগুলো সমদশা সম্পন্ন।
সুতরাং পর্দার ay,a,a বিন্দুগুলো চরম বিন্দু এবং এই বিন্দুগুলো উজ্জ্বল দেখাবে। দুটি পাশাপাশি সমদশা সম্পন্ন বিন্দুর মধ্যবর্তী দূরত্বকে তরঙ্গদৈর্ঘ্য (2) বলে। তাই সমদশা সম্পন্ন বিন্দুগুলোর মধ্যে মধ্যবর্তী দূরত্বকে অবশ্যই A এর পূর্ণগুণিতক হবে। সুতরাং O থেকে পর্দার যে যে বিন্দু nă হবে সেই সেই বিন্দু উজ্জ্বল দেখাবে। এখানে n = 0, 1, 2, 3, 4…… ।
অপর দিকে ) হতে পর্দা পর্যর্ল্ড Ob, Ob, Ob, Ob, রেখাগুলো অনুতরঙ্গের সেই সব বিন্দু দিয়ে গেছে যে সব বিন্দুতে একটি তরঙ্গ শীর্ষ ও একটি তরঙ্গ পাদ পরস্পরকে ছেদ করেছে। অর্থাৎ ছেদবিন্দুগুলো বিপরীতদশা সম্পন্ন। সুতরাং পর্দার ao,a,a বিন্দুগুলো অবম বিন্দু এবং এই বিন্দুগুলো অন্ধকার দেখাবে। একটি তরঙ্গ শীর্ষ ও তরঙ্গ পাদ এর মধ্যবর্তী দূরত্ব হলো λ 2 । তাই বিপরীতদশা সম্পন্ন বিন্দুগুলোর মধ্যে মধ্যবর্তী দূরত্বকে অবশ্যই এর পূর্ণগুণিতক হবে।
সুতরাং O থেকে পর্দার যে যে বিন্দু (2n+1)/2 হবে সেই সেই বিন্দু অন্ধকার দেখাবে। এখানে n = 0,1,2,3,4…… ।
ব্যতিচারের গাণিতিক ব্যাখ্যা (Mathematical Analysis of Interference):
মনে করি, খুব কাছাকাছি d দূরত্বে অবস্থিত S1 ও S2 চিড় দুটি প্রকৃত পক্ষে সুসংহত, সমতরঙ্গ দৈর্ঘ্য সম্পন্ন ও একবর্ণী আলোক উৎস হিসাবে কাজ করছে (চিত্র)। এদের মধ্যবিন্দু O এবং OO1 হলো মধ্য রেখা। উৎস দুটি হতে দুটি আলোক রশ্মি D দূরত্বে অবস্থিত পর্দায় P বিন্দুতে আপতিত হলে। ধরি, S1 ও S2 চিড় দুটি হতে P বিন্দুর দুরত্ব যথাক্রমে r1 ও r2। O হতে P বিন্দুর দুরত্ব,r অর্থাৎ (r1 + r2)/2 = r (গড় দূরত্ব)।

ধরি, S1 ও S2 চিড় দুটি হতে উৎপন্ন দুটি আলোক তরঙ্গ যার প্রতিটির বিড়ার a এবং তরঙ্গদৈর্ঘ্য λ । তরঙ্গ দুটি P বিন্দুতে উপরিপাতিত হলো। S1 ও S2 উৎস থেকে সৃষ্ট তরঙ্গের জন্য সময়ে P বিন্দুর সরণ,
y1 = asin(2π/λ(ct-r₁) ………………………..(1)
এবং y2 = asin(2π/λ(ct-r2) ………………………..(2)
তরঙ্গ দুটির দশা পার্থক্য, ∆∂ = 2π/ λ (ct-r1) – 2π/ λct-r2)
বা, ∆δ = 2π/ λ (r2-r1)
বা, ∆δ = 2π/ λ∆r ………………………..(3)
উপরিপাতন নীতি অনুসারে,
y = y₁ + y2 = asin2π/ λ (ct-r1) – a sin2π/ λ(ct-r2)
বা, y = 2a sin2π/λ (ct-r1+ct− r2)/2 cos2π/λ(ct-r1−ct +r2)/ 2
বা, y=2a sin2π/λ( ct – (r1+ r2)/2)cos2π/λ(r2− r1)/ 2
ধরি, (r1+ r2)/2 = r (গড় দূরত্ব) এবং (r2− r1)/ 2 = ∆r (পথ পার্থক্য)
অতএব, y = 2asin2π/ λ (ct-r)2π/λ.∆r/2
বা, y=Asin 2π/ λ(ct-r) ………………………..(4)
এখানে, A = 2acos2π/λ.∆r/2 ………………………..(5)
এখানে, A = 2acos2π/λ.∆r/2 হলো লব্ধি তরঙ্গের বিস্তার।
বিরের বর্গ করলে, A2 = 4a2 cos2π∆r/λ
যেহেতু প্রাবল্য বিারের বর্গের সমানাতিক অর্থাৎ I α A2
অতএব, I = k4a2cos2π∆r/λ
ধরি, Io =k4a2
অতএব, I = Io cost2π∆r/λ ………………………..(6)
আবার, 1 নং সমীকরণকে লেখা যায়, ∆r = λ/2π∆δ
অতএব, I = Io cos2π/λ x λ/2π∆δ
বা, I = Io cos2∆δ/2 ………………………..(7)
এখন, I কে Y-অক্ষে এবং ∆δ কে X-অক্ষে নিয়ে লেখ চিত্র অঙ্কন করা হলে চিত্রানুরূপ একটি বক্র রেখা পাওয়া যাবে। বক্র রেখাটি দশা পার্থক্যের সাথে তীব্রতার পরিবর্তন নির্দেশ করে । আপাত দৃষ্টিতে মনে হতে পারে, আলোর ব্যতিচারে শক্তির নিত্যতা সূত্র মেনে চলে না। কিন্তু প্রকৃত পক্ষে এখানে শক্তির বিনাশ হয় না বরং শক্তির পুনর্বন্টন হয়। a বিস্তৃরের দুটি আলোক তরঙ্গ ব্যতিচার না ঘটালে পর্দায় প্রাবল্য সর্বত্র ka2 + ka2 = 2ka2 হতো। কিন্তু গঠনমূলক ব্যতিচারে তরঙ্গের বিস্তৃর 2a তাই তীব্রতা 4ka2 এবং ধ্বংসাত্মক ব্যতিচারে তরঙ্গের বিস্তৃর O( তাই প্রাবল্য O । অতএব গড় প্রাবল্য Iav = (4ka2+0)/2 = 2ka2 ।
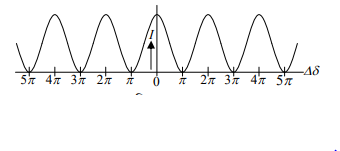
সুতরাং, ব্যতিচারের ফলে শক্তি ধ্বংস হয়নি, পূনর্বণ্টিত হয়েছে মাত্র।
উদাহরণ ১ :
একটি তরঙ্গের দুটি বিন্দুর মধ্যে পথ পার্থক্য । বিন্দুদ্বয়ের মধ্যে দশা পার্থক্য কত ?
সমাধান:
দেওয়া আছে, ∆r = λ/4 এবং ∆δ = ?
আমরা জানি,
∆δ = 2π/λ∆r
মান বসালে, ∆δ = 2π/λ x λ /4 = π/2
উ: π/2
উদাহরণ ২ :
ইয়ং এর দ্বি চিড় ব্যবহৃত আলোক তরঙ্গের বিস্তৃর 800Å । যখন আলোরশ্মিদ্বয়ের পর্দার কোনো বিন্দুতে উপরিপাতন ঘটে তখন এদের পথ পার্থক্য 2/3λ । ঐ বিন্দুতে লব্ধি তরঙ্গের বিস্তৃর নির্ণয় করন।
সমাধানঃ
দেয়া আছে, a = 800Å = 8×10^-8m, ∆r= 2/3 λ এবং A = ?
আমরা জানি,
লব্ধি তরঙ্গের বিস্তৃর, A = 2acos2π/λ.∆r/2
মান বসালে, A = 2 x 8 x 10-8 x cos 2 x π/λ.∆r/2
বা, A = 16×10-8 x cos2 x π/3 = 16×10-8 × 0.999 = 15.98×10-8 m
উ : 15.98×10-8 m
সার-সংক্ষেপ :
উপরিপাতন নীতি:
তরঙ্গ প্রবাহের ফলে মাধ্যমের কণাগুলো আন্দোলিত হয়। কোন মাধ্যমের মধ্য দিয়ে একাধিক তরঙ্গ সঞ্চালিত হলে কোনো কণা বা বিন্দুর লব্ধি-সরণ ঘটবে। এ লব্ধি-সরণ তরঙ্গগুলো কর্তৃক পৃথক পৃথক সরণের ভেক্টর যোগফলের সমান। একে তরঙ্গের উপরিপাতন নীতি বলে।
সুসঙ্গত উৎস:
যদি দুটি আলোক উৎস থেকে সব সময় একই দশার বা একই দশা পার্থক্যের তরঙ্গ নির্গত হয় তবে আলোক উৎস দুটিকে সুসংগত উৎস বলে ।
ব্যতিচার:
দুটি আলোক উৎস থেকে একই বিড়ারের এবং একই তরঙ্গ দৈর্ঘ্যের আলো নির্গত হয়ে কোন বিন্দুতে আপতিত হলে উপরিপাতনের ফলে কোথাও উজ্জ্বল এবং কোথাও অন্ধকার সৃষ্টি হয়। আলোর এই উজ্জ্বলতার হ্রাস-বৃদ্ধির ঘটনাকে ব্যতিচার বলে। সমদশা সম্পন্ন আলো রশ্মির উপরিপাতনের ফলে উজ্জ্বল বা চরম এবং বিপরীত দশা সম্পন্ন আলো রশ্মির উপরিপাতনের ফলে অন্ধকার বা অবম-এর সৃষ্টি হয়। এটি একটি অবস্থানিক ঘটনা।
বহুনির্বাচনী প্রশ্নঃ
১। একই তরঙ্গদৈর্ঘ্যের দুটি আলোক উৎসে দশা পার্থক্য সর্বদা সমান থাকলে তাকে বলে
ক. গৌণ উৎস
খ. সুসংগত উৎস
গ. অসমবর্তিত উৎস
ঘ. সমবর্তিত উৎস
২। উপরিপাতনের ফলে ব্যাতিচার ঘটানোর শর্তানুসারে
i. আলোক উৎস দুটি একই তরঙ্গদৈর্ঘ্যের সুসংগত হতে হবে।
iii. তরঙ্গ উৎস দুটি খুব কাছাকাছি হতে হবে।
ii. তরঙ্গ দুটির বিড়ার সমান হতে হবে।
কোনটি সঠিক?
ক. i ও ii
খ. ii ও iii
গ. i ও iii
ঘ. i, ii ও iii
