গাউসের সূত্র

আজকের আলোচনার বিষয়: গাউসের সূত্র। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ১ স্থির তড়িৎ এর অন্তর্ভুক্ত।

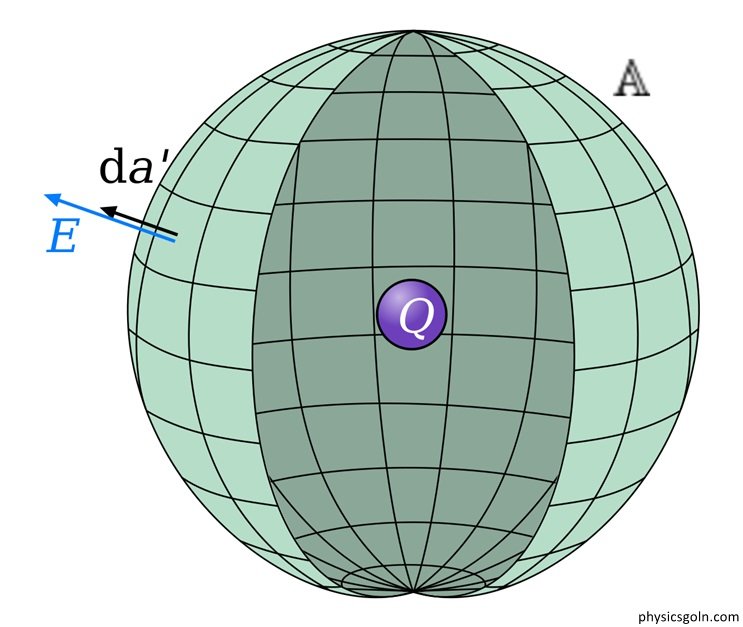
গাউসের সূত্র

জার্মান বিজ্ঞানী কাল ফ্রেডরিক গাউস (১৭৭৭-১৮৫৫) তড়িৎ ফ্লাক্স এবং তড়িতাধানের মধ্যে একটি গুর“ত্বপূর্ণ সূত্র প্রদান করেন। সূত্রটির সাহায্যে কোনো একটি বদ্ধ তলের বিভিন্ন বিন্দুতে তড়িৎ প্রাবল্য নির্ণয় করা যায়। সুত্রটি বিবৃত করার আগে তড়িৎ ফ্লাক্স, ক্ষেত্র ভেক্টর ও গাউসীয় তল সম্পর্কে জানা প্রয়োজন ।

ক্ষেত্র ভেক্টর (Area Vector) :

কোনো পৃষ্ঠতলের ক্ষেত্রফলকে পদার্থবিজ্ঞানে বিভিন্ন ক্ষেত্রে একটি ভেক্টর দিয়ে গণ্য করা হয়। ক্ষেত্র ভেক্টরটির দৈর্ঘ্য দ্বারা তলটির ক্ষেত্রফলের মান সূচিত হয়। ক্ষেত্র ভেক্টরটির অভিমুখ ধরা হয় তলটির লম্ব বরাবর।

গাউসীয় তল (Gaussian Surface) :

একটি আধানের চারদিকে কল্পিত বদ্ধ তলকে গাউসীয় তল বলে। গাউসীয় তল যে কোনো আকৃতির হতে পারে ।
তড়িৎ ফ্লাক্স (Elecric Flux) : তড়িৎ ক্ষেত্রের কোনো তলের ক্ষেত্রফলের সাথে ঐ তলের লম্ব বরাবর তড়িৎ ক্ষেত্রের তথা তড়িৎ ক্ষেত্রের প্রাবল্যের উপাংশ গুণ করলে তড়িৎ ফ্লাক্স পাওয়া যায়।

অন্য কথায় কোনো তলের ক্ষেত্রফল এবং ঐ তলের লম্ব বরাবর তড়িৎ ক্ষেত্রের উপাংশের গুণফলকে ঐ তলের সাথে সংশিপ্টষ্ট তড়িৎ ফ্লাক্স বলে ।

কোনো তলের ক্ষেত্রফল S এবং তড়িৎ ক্ষেত্র É তলের সাথে ৪ কোণে ক্রিয়া করে [চিত্র : ১.২৩]। তলের লম্ব বরাবর তড়িৎ ক্ষেত্রের উপাংশ হবে Ecose ।

সুতরাং তড়িৎ ফ্লাক্স হবে,

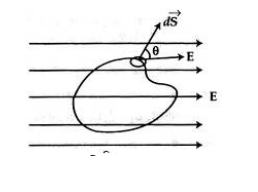
∅ = (Ecost ) S = Escost

= E.S.  ………………(1)

কোনো তড়িৎ ক্ষেত্র Ē তে একটি ক্ষুদ্র তল ds নেয়া হলো [চিত্র]। তাহলে ঐ তলের তড়িৎ ফ্লাক্স হবে-

d∅ = E.ds ………………(2)

সমগ্র ক্ষেত্রফল S এর জন্য তড়িৎ ফ্লাক্স হবে,

∅ = ∫E.ds ………………(3)

সমগ্র বদ্ধ তলের জন্য ঐ ক্ষেত্রের ফ্লাক্স হবে,

∅ = ∮E.ds ………………(3)

∮ প্রতীকটি সমগ্র বদ্ধ তলের জন্য সমাকলন বোঝায় ।

রাশি ও একক :

তড়িৎ ফ্লাক্স একটি স্কেলার রাশি এবং এর S I একক হচ্ছে NC-1m2 ।

গাউসের সূত্র (Gauss’s Law) :

কোনো তড়িৎ ক্ষেত্রে কোনো বদ্ধ কল্পিত তলের (গাউসীয় তল) তড়িৎ ফ্লাক্সের ६, গুণ এবং ঐ তল দ্বারা বেষ্টিত মোট তড়িতাধান সমান।

ব্যাখ্যা :

যদি কোনো বদ্ধ তলের ক্ষেত্রফল S এবং ঐ তল দ্বারা বেষ্টিত মোট আধানের পরিমাণ q হয়, তাহলে গাউসের সূত্রানুসারে,

εo∅ = q ………………(4)

বা, εo∮ E.ds = q ………………(5)

এখানে εo হচ্ছে শূন্যস্থানের ভেদনযোগ্যতা।

যদি ঐ তলে (গাউসীয় তল) কোনো আধান আবদ্ধ না থাকে বা তাতে সমপরিমাণ ধনাত্মক ও ঋণাত্মক আধান থাকে তাহলে q= 0 হয়

সুতরাং তড়িৎ ফ্লাক্স ∅ = ∮ E.ds = 0

কুলম্বের সূত্র হতে গাউসের সূত্র প্রতিপাদন (Derivation of Gauss’s Law from Coulomb’s Law)

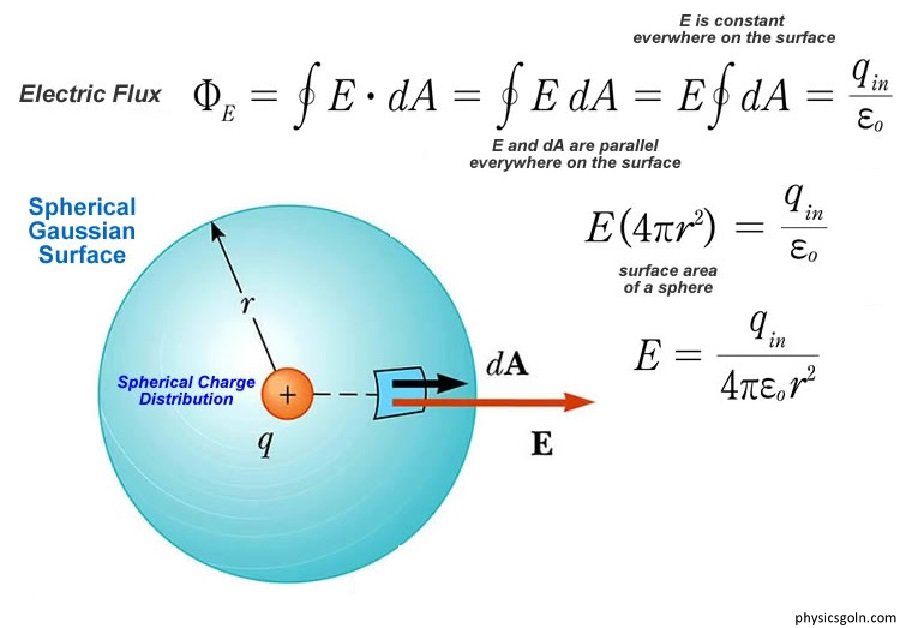
ধরা যাক, A বিন্দুতে একটি বিচ্ছিন্ন বিন্দু আধান q অবস্থিত [চিত্র ১.২৪]। q আধান তার চারদিকে একটি তড়িৎ ক্ষেত্র সৃষ্টি করবে। এখন q বিন্দু থেকে r দূরত্বে তড়িৎ ক্ষেত্রের মধ্যে B বিন্দুতে অপর একটি একক আধান রাখি। কুলম্বের সূত্রানুসারে [সমীকরণ (১.২)] এ একক আধানটি যে বল অনুভব করবে, তাই হচ্ছে B বিন্দুর তড়িৎ প্রাবল্য E।

E= (1/4πεo).(q/r2)

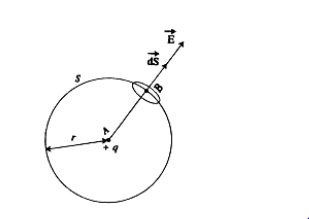
E এর দিকে হবে AB রেখা বরাবর এবং বহির্মুখী। q কে কেন্দ্র করে r ব্যাসার্ধের একটি গোলক কল্পনা করি। এ গোলকের পৃষ্ঠে সর্বত্র তড়িৎ ক্ষেত্র É এর তথা তড়িৎ প্রাবল্যের মান সমান হবে এবং দিক হবে ব্যাসার্ধ বরাবর বহির্মুখী । এখন B বিন্দুতে গোলকের অতি ক্ষুদ্র একটি তল কল্পনা করি। ধরা যাক, ক্ষুদ্র তল ds এবং এর মান হচ্ছে ঐ তলের ক্ষেত্রফল, দিক হচ্ছে ঐ তলের লম্ব বরাবর বহির্মুখী। আমরা জানি, গোলকের পৃষ্ঠের প্রতিটি বিন্দুতে Ē এর দিক ব্যাসার্ধ  বরাবর বহির্মুখী । সুতরাং গোলকের পৃষ্ঠের প্রতিটি বিন্দুতে Ē এবং ds এর দিক একই অর্থাৎ Ē এবং ds এর দিক একই অর্থাৎ É এবং ds এর মধ্যবর্তী কোণ t = 0° ।

এখন ds তলের সাথে সংশিষ্ট তড়িৎ ফ্লাক্স হবে, d∅ = E.ds

সুতরাং গোলকের পৃষ্ঠের সমগ্র বদ্ধতল S-এর কাজ মোট ফ্লাক্স,

∅ = ∮E.ds

= ∮E.dscose

= ∮(1/4πεo).(q/r2).dS cos 0°

= q/4πεor2 ∮dS ………………(6)

আবার r ব্যাসাধের গোলকের পৃষ্ঠের ক্ষেত্রফল,

∮dS = 4πr2

সুতরাং (6) সমীকরণ থেকে পাই-

∅ = 1/4лε0r² x4πr2

∅ = q /ε0 ……………..(7)

ε0∮E.ds = q  ……………..(8)

উপরের সমীকরণ থেকে দেখা যায় যে, তড়িৎ ক্ষেত্রের কোনো বদ্ধতলের তড়িৎ ফ্লাক্সের ৪ গুণ ঐ তল দ্বারা আবদ্ধ মোট আধানের সমান।

সমীকরণে (7 এবং (8)-ই হলো গাউসের সূত্র সুতরাং কুলম্বের সূত্র থেকে গাউসের সূত্র প্রতিপাদিত হলো ।

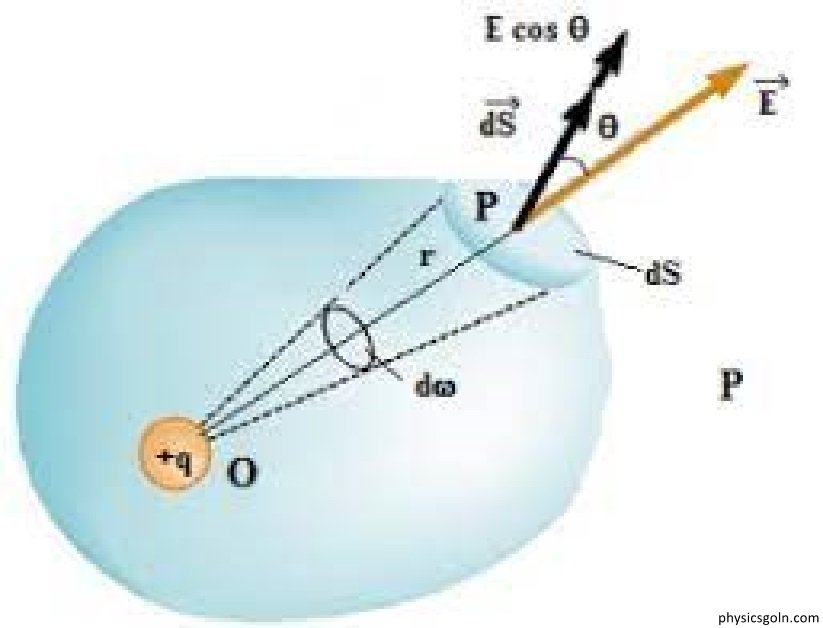
 গাউসের সূত্র থেকে কুলম্বের সূত্র প্রতিপাদন
(Deduction of Coulomb’s Law from Gauss’s Law)

A বিন্দুতে একটি বিন্দু আধান q বিবেচনা করা যাক, q কে কেন্দ্র করে r ব্যাসার্ধের একটি গোলক কল্পনা করি। এ গোলকের পৃষ্ঠে সর্বত্র তড়িৎ ক্ষেত্র É এর তথা তড়িৎ প্রাবল্যের মান সমান হবে এবং দিক হবে ব্যাসার্ধ বরাবর বহির্মুখী চিত্র ]। সুতরাং গোলক পৃষ্ঠের প্রতিটি বিন্দুতে Ē এবং ds এর দিক একই অর্থাৎ É এবং ds এর মধ্যবর্তী কোণ B = 0° । গাউসের সূত্রানুযায়ী আমরা পাই,

ε0∮E.ds = q ……………..(9)

এখানে, Ē এবং ds এর মধ্যবর্তী কোণ t =0°

সুতরাং ∮E.ds = ∮ Eds cos 0° = E∮ds = E × 4πr2

যেহেতু r ব্যাসার্ধের গোলকের পৃষ্ঠের ক্ষেত্রফল ∮ds = 4πr2

সুতরাং সমীকরণ (9) থেকে পাই-

ε0E4πr2 = q

বা, E = 1/4πε0. q/r2

এখন যে বিন্দুতে তড়িৎ প্রাবল্য E এর মান নির্ণয় করা হয়েছে, সে বিন্দুতে একটি আধান qo স্থাপন করি। তাহলে q0 এর ওপর প্রযুক্ত বলের মান

F = qoE

= 1/4πε0 .qqo/r2 ……………..(10)

উপরের সমীকরণ থেকে দেখা যায়, নির্দিষ্ট মাধ্যমে দুটি আধানের মধ্যকার ক্রিয়াশীল বলের মান আধানদ্বয়ের গুণফলের সমানুপাতিক এবং তাদের মধ্যকার দূরত্বের বর্গের ব্যানুপাতিক, এটিই কুলম্বের সূত্র।

সুতরাং কুলম্বের সূত্র গাউসের সূত্র হতে প্রতিপাদিত হলো।

কুলম্বের সূত্রের সীমাবদ্ধতা (Limitations of Coulomb’s Law)

কুলম্বের সূত্র স্থির তড়িতের একটি উলেণ্ঢখযোগ্য সূত্র। তবু কুলম্বের সূত্রের কিছু সীমাবদ্ধতা আছে। নিচে কুলম্বের সূত্রের সীমাবদ্ধতাগুলো উলেখ করা হলো।

১. কুলম্বের সূত্র শুধুমাত্র বিন্দু আধানের জন্য প্রযোজ্য। যেকোনো অনিয়মিত আকারের আহিত বস্তুর ক্ষেত্রে এ সূত্র প্রয়োগ করা জটিল, যেহেতু বস্তুর কেন্দ্র সঠিকভাবে নির্ণয় করা যায় না।

২. কুলম্বের সূত্রটি শুধুমাত্র আহিত স্থির বস্তু আধানের জন্য প্রযোজ্য। এ সূত্রটি গতিশীল আধানের জন্য সঠিকভাবে প্রয়োগ করা যায় না।

৩. আধান দুটির আকৃতি এদের মধ্যকার দূরত্বের চেয়ে অনেক কম হলে, সেক্ষেত্রে কুলম্বের সূত্র প্রযোজ্য। আধানদ্বয় বড় হলে তড়িৎ বলের উপর মহাকর্ষ বল ক্রিয়া করবে।

সার-সংক্ষেপ :

ক্ষেত্র ভেক্টর :

কোনো পৃষ্ঠতলের ক্ষেত্রফলকে পদার্থবিজ্ঞানে বিভিন্ন ক্ষেত্রে একটি ভেক্টর দিয়ে গণ্য করা হয়। ক্ষেত্র ভেক্টরটির দৈর্ঘ্য দ্বারা তলটির ক্ষেত্রফলের মান সূচিত হয়। ক্ষেত্র ভেক্টরটির অভিমুখ ধরা হয় তলটির লম্ব বরাবর।

গাউসীয় তল :

একটি আধানের চারদিকে কল্পিত বদ্ধ তলকে গাউসীয় তল বলে। গাউসীয় তল যে কোনো আকৃতির হতে পারে।

তড়িৎ ফ্লাক্স :

তড়িৎ ক্ষেত্রের কোনো তলের ক্ষেত্রফলের সাথে ঐ তলের লম্ব বরাবর তড়িৎ ক্ষেত্রের উপাংশের গুণফলকে ঐ তলের সাথে সংশিশ্চষ্ট তড়িৎ ফ্লাক্স বলে।

গাউসের সূত্র :

কোনো তড়িৎ ক্ষেত্রে কোনো বদ্ধ কল্পিত তলের (গাউসীয় তল) তড়িৎ ফ্লাক্সের ৪ গুণ এবং ঐ তল দ্বারা বেষ্টিত মোট তড়িতাধান সমান ।

গাণিতিক উদাহরণ-১

একটি সর— দরে দৈর্ঘ্য 3m। দটি 6uC আধানের দ্বারা সুষমভাবে আহিত হলে ( 1 ) দীটির একক দৈর্ঘ্যে আধানের পরিমাণ এবং (ii) দ ेটির কেন্দ্র থেকে 2m দূরে কোনো বিন্দুতে তড়িৎ প্রাবল্য নির্ণয় করন।

এখানে,

তারের দৈর্ঘ্য, 1 = 3m,

আধান, q = 6uC = 6×10°C,

দূরত্ব, r = 2m

ε0 = 8.85×10-12 C2Nm2

8=?
E = ?

আমরা জানি,

(i) দ―টির একক দৈর্ঘ্য আধানের পরিমাণ,

λ= q/l = 6×10-6/ 3 =2×10^6 Cm-1

(ii) তড়িৎ প্রাবল্য,

E = 1/2πε0.⋏/r

বা, E= 1×2×10^6 Cm-1/ 2×3.14×8.85×10-12C2N-1m-2 × 2m

=2/ 2 x 3.14 × 8.85 × 2 × 106 NC-1

= 1 /55.58 x106NC-1

= 1.80×104 NC-1

উ: 1.80 × 104 NC-1