আজকে আমরা গাউসের সূত্রের ব্যবহার সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ১ স্থির তড়িৎ এর অন্তর্ভুক্ত।
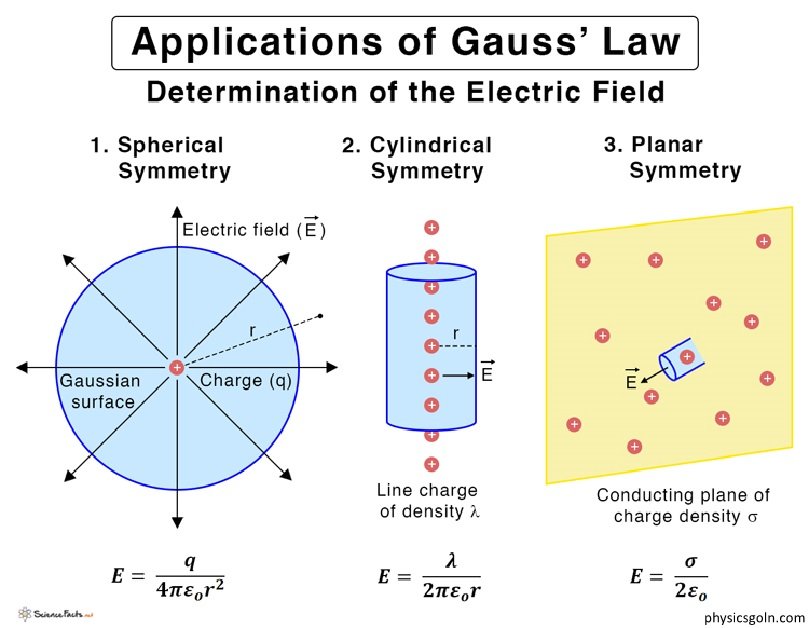
গাউসের সূত্রের ব্যবহার
অসীম দৈর্ঘ্যের একটি সরল ও সুষম আহিত দরে জন্য এর নিকটে তড়িৎ ক্ষেত্র তথা তড়িৎ প্রাবল্য
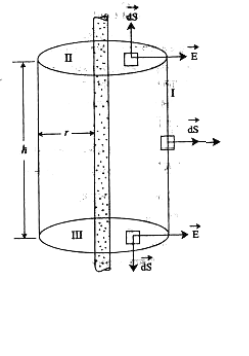
মনে করি, অসীম দৈর্ঘ্যের সরল ও সুষম একটি আহিত দরে প্রতি একক দৈর্ঘ্যের সর্বত্র আধানের পরিমাণ সমান এবং (চিত্র) সুষম আহিত দ থেকে সমান দূরে অবস্থিত প্রতিটি বিন্দুতে তড়িৎ ক্ষেত্র প্রাবল্য E এর মান সমান এবং এর দিক হবে ব্যাসার্ধ বরাবর বহির্মুখী। সুষম আহিত দটির অক্ষকে, অক্ষ ধরে একটি h দৈর্ঘ্যের এবং r ব্যাসার্ধের সিলিন্ডার কল্পনা করি (চিত্র)। সিলিন্ডারের পৃষ্ঠ গাউসীয় তল হিসেবে বিবেচনা করা হবে।
এমতাবস্থায়, সিলিারে আবদ্ধ মোট আধান অর্থাৎ দরে । দৈর্ঘ্যের মধ্যে মোট আধানের পরিমাণ হলো, q = ⋏h
মনে করি, সিলিস্টারের দুই প্রাড় সমতল পৃষ্ঠ দ্বারা আবদ্ধ। যেহেতু সিলিন্ডারের বক্র পৃষ্ঠের প্রত্যেকটি বিন্দুই দ ेের আধান থেকে সমান দূরে অবস্থিত সুতরাং সিলিারের বক্র পৃষ্ঠের সকল বিন্দুতে É এর মান ধ্রুব। প্রত্যেকটি বিন্দুতে Ē বক্রতলের সাথে লম্ব বরাবর বহির্মুখী।
সমীকরণ (5) থেকে পাই-
εo∮ E.ds = q
যদি গাউসীয় তলকে তিনটি অংশ I, II ও III করা যায় (চিত্র), তবে,
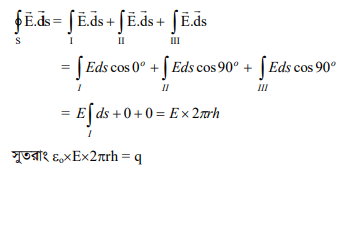
আমরা জানি, q = ⋏h
E= 1 /2πεo ⋏/h ………………(1)
সুষমভাবে আহিত একটি গোলাকার খোলকের জন্য তড়িৎ প্রাবল্য
(ক) খোলকের বাইরে কোনো বিন্দুতে তড়িৎ প্রাবল্য
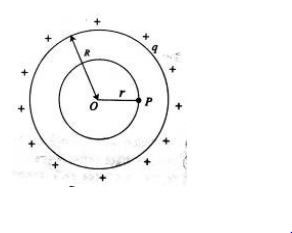
মনে করি, R ব্যাসার্ধের একটি গোলাকার খোলকের কেন্দ্র O। এ খোলকের পৃষ্ঠে q ধনাত্মক আধান সুষমভাবে বণ্টিত আছে। খোলকের বাইরে P একটি বিন্দু। P বিন্দুতে তড়িৎ প্রাবল্য নির্ণয় করতে হবে। O বিন্দুকে কেন্দ্র করে OP = r (এখানে r>R) ব্যাসার্ধ ধরে, একটি গোলক কল্পনা করি, যার পৃষ্ঠ হবে গাউসীয় তল (চিত্র ১.২৬)। এই গাউসীয় তলের প্রত্যেক বিন্দুতে তড়িৎ প্রাবল্য E এর মান সমান এবং দিক হবে ব্যাসার্ধ বরাবর বহির্মুখী।
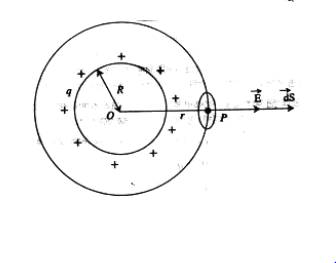
সমীকরণ (8) থেকে পাই,
ε0∮E.ds = q
এক্ষেত্রে É ও ds এর মধ্যবর্তী কোণ t =0°
:. ε0∮E.ds cos 0° = q
ε0∮E.ds = q
ε0E* 4πr2 = q
E = 1/4πεo.q/r2 ………………(2)
(খ) খোলকের পৃষ্ঠে কোনো বিন্দুতে তড়িৎ প্রাবল্য
খোলকের ওপর কোনো বিন্দুতে r =R
সমীকরণ (2)-এ r এর পরিবর্তে R বসিয়ে পাই-
E = 1/4πεo.q/R2
বা, E = 1/εo .q/4πR2 ………………(3)
তলমাত্রিক ঘনত্বের সংজ্ঞানুসারে আমরা জানি-
তলমাত্রিক ঘনত্ব, σ = q/4лR2
E = σ/εo
(গ) খোলকের অভ্যস্ত্বরে কোনো বিন্দুতে তড়িৎ প্রাবল্য
মনে করি, গোলকের অভ্যস্ত্ররে P একটি বিন্দু। O বিন্দুকে কেন্দ্র করে OP =r (r<R) ব্যাসার্ধ নিয়ে একটি গোলক কল্পনা করি, (চিত্র ১.২৭)। এই গোলকের পৃষ্ঠই এই ক্ষেত্রে গাউসীয় তল। সেহেতু গাউসীয় তল দ্বারা কোনো আধান আবদ্ধ নেই। সুতরাং q = 0
সমীকরণ অনুসারে গসের সূত্র থেকে পাই।
ε0∮E.ds = 0
E=0
সুতরাং কোনো আহিত গোলাকার খোলকের অভ্যস্ত্বরে কোনো বিন্দুতে তড়িৎ প্রাবল্য শূন্য । সুষমভাবে আহিত একটি নিরেট গোলকের জন্য তড়িৎ প্রাবল্য শূন্য।
(ক) নিরেট গোলকের বাইরে কোনো বিন্দুতে তড়িৎ প্রাবল্য
মনে করি, R ব্যাসার্ধের একটি গোলকের কেন্দ্র 0। গোলকটি q আধানে সুষমভাবে আহিত। গোলকের বাইরে P একটি বিন্দু । O বিন্দুকে কেন্দ্র করে OP = 1 (এখানে r>R ) ব্যাসার্ধ ধরে, একটি গোলক কল্পনা করি, যার পৃষ্ঠ হবে গাউসীয় তল (চিত্র ১.২৮)।
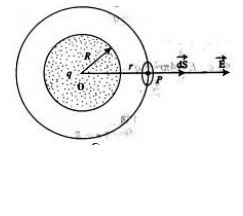
P বিন্দুতে গাউসীয় তলের ক্ষুদ্রাতিক্ষুদ্র অংশ ds বিবেচনা করি যার দিক ব্যাসার্ধ বরাবর বহির্মুখী । P বিন্দুতে তড়িৎ প্রাবল্য
E নির্ণয় করতে হবে যার দিক হবে ব্যাসার্ধ বরাবর বহির্মুখী। সুতরাং গাউসের সূত্র থেকে পাই-
ε0∮E.ds = q যেহেতু É এবং ds একই দিকে ক্রিয়া করে সুতরাং এদের অন্তর্ভুক্ত কোণ t=0° হবে,
ε0∮E.ds cos 0° = q
ε0∮E.ds cos 0° = q
ε0E∮ds = q
ε0E x 4πr2 = q
E= 1/4πε0.q/ r²
(খ) নিরেট গোলকের পৃষ্ঠে কোনো বিন্দুতে তড়িৎ প্রাবল্য গোলকের পৃষ্ঠে r =R
E= 1/4πε0.q/ R²
(গ) নিরেট গোলকের অভ্যন্ড্ররে কোনো বিন্দুতে তড়িৎ প্রাবল্য
মনে করি, R ব্যাসার্ধের একটি গোলকের কেন্দ্র O। গোলকটি q আধানে সুষমভাবে আহিত, গোলকের অভ্যস্ত্ররে P একটি বিন্দু । O বিন্দুকে কেন্দ্র করে OP = r (এখানে r<R) ব্যাসার্ধ ধরে, একটি গোলক কল্পনা করি, যার পৃষ্ঠ গাউসীয় তল (চিত্র ১.২৯)। P বিন্দুতে গাউসীয় তলের ক্ষুদ্রাতিক্ষুদ্র অংশ ds বিবেচনা করি যার দিক ব্যাসার্ধ বরাবর বহির্মুখী। P বিন্দুতে তড়িৎ প্রাবল্য É নির্ণয় করতে হবে যার দিক হবে ব্যাসার্ধ বরাবর বহির্মুখী। সুতরাং গাউসের সূত্র প্রয়োগ করে আমরা পাই-
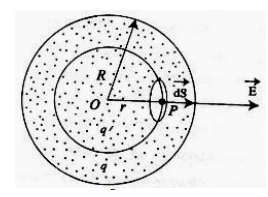
ε0∮E.ds = q’ ………………(3)
এখানে q’ হচ্ছে r ব্যাসার্ধের গোলকের অভ্যন্ড্ররের মোট আধান, আমরা জানি, R ব্যাসাধের নিরেট গোলকে q আধান সুষমভাবে বণ্টিত। সুতরাং গোলকের প্রতি একক আয়তনে আধানের পরিমাণ,
P = গোলকের আধান /R ব্যাসার্ধের গোলকের আয়তন = q/(4/3πR3)
r ব্যাসার্ধের গোলকে মোট আধান q’ হবে,
q = p x r ব্যাসার্ধের গোলকের আয়তন
=p x-4/3πr3 = q/(4/3πR3) X 4/3πr3
q’ = r3/R3.q
সমীকরণ তথা গাউসের সূত্র থেকে পাই,
ε0∮E.ds = r3/R3q
যেহেতু E এবং ds এর দিক একই দিকে ক্রিয়া করে সুতরাং এদের অন্তর্ভুক্ত কোণ t = 0° হবে,
ε0∮E.ds cos 0° = r3/R3q
বা, ε0∮E.ds cos 0° = r3/R3q
বা, ε0∮E.ds = r3/R3q
বা, ε0∮E.ds 4πr² = r3/R3q
E = r3q/4πε0r2R3
E = q/4πε0.r/R3 ………………(3)
গাণিতিক উদাহরণ-১
একটি নির্দিষ্ট স্থানে একটি তড়িৎক্ষেত্র হলো, É = (3i + 2 j – 2k ) × 102 NC + । এই ক্ষেত্রের জন্য (2i-j) × 102m2 ক্ষেত্রফলের মধ্য দিয়ে অতিক্রাড় তড়িৎ ফ্লাক্স নির্ণয় করন।
আমরা জানি,
এখানে,
তড়িৎক্ষেত্রের প্রাবল্য,
E = (3i + 2j – 2k) × 10NC
ক্ষেত্রফল, AS = (2i – j) x10 2m 2
∆∅ = E.∆S
= { (3i + 2 j – 2k) x 10′ }{2i – j) x10 2 }
= (3×2-2×1-2×0) × 103
তড়িৎ ফ্লাক্স, p = 4x10NC-1m2
উত্তরঃ 4×103 NC-‘m²
গাণিতিক উদাহরণ-২।
একটি সুষম তড়িৎ ক্ষেত্রের তড়িৎ প্রাবল্য, É = (6i + 4j – 4k)NC-1 । তড়িৎ ক্ষেত্রের YZ তলে স্থাপিত 20m2 ক্ষেত্রফল বিশিষ্ট একটি তলে তড়িৎ ফ্লাক্স নির্ণয় করন।
এখানে,
তড়িৎক্ষেত্রের প্রাবল্য, É = (61 + 4j + 4k)NC-1
ক্ষেত্রফলের মান, AS = 2m²
ক্ষেত্রফল ভেক্টর, AS = 20jm2
তড়িৎ ফ্লাক্স, Ap=?
আমরা জানি,
যেহেতু তলটি YZ তলে অবস্থিত সেহেতু তলের দিক হবে x অক্ষ বরাবর ।
:: YZ তলে স্থাপিত ক্ষেত্রের মধ্যদিয়ে ফ্লাক্স = X – অক্ষ বরাবর প্রাবল্য XYZ তলের ক্ষেত্রফল (ds)
বা, ∅ = ExdS
= (6i + 4j + 4k) (201)
=6×20+4×0+4×0
:. তড়িৎ ফ্লাক্স, ∆∅=120NC1m2
উ: 120NC-1m2
