গ্যালিলিও রূপান্তর

আজকে আমরা গ্যালিলিও রূপান্তর সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৮ এর  আধুনিক পদার্থবিজ্ঞান এর অন্তর্ভুক্ত।

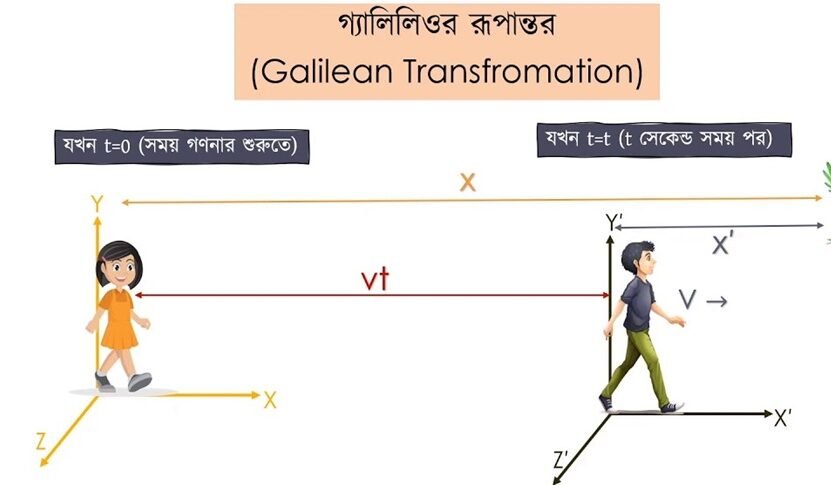
 গ্যালিলিও রূপান্তর

যদি কোনো ঘটনা একই সাথে দুটি পৃথক জড় প্রসঙ্গ কাঠামো থেকে পর্যবেক্ষণ করা হয় যখন কাঠামো দুটি পরস্পরের সাথে । বেগে X-অক্ষ বরাবর গতিশীল, তবে স্বাভাবিক ভাবেই দুটি কাঠামোতে দুই প্রকার দুই সেট স্থানাংক পাওয়া যাবে। উক্ত ঘটনার জন্য দুই সেট স্থানাংকের মধ্যে সম্পর্ক স্থাপনের জন্য যে সমীকরণ পাওয়া যায় তাকে গ্যালিলিও রূপান্তর সমীকরণ বলে। আমরা বাড়বে যে ঘটনাগুলো পর্যবেক্ষণ করি এবং অনুভব করি গ্যালিলিও রূপান্তর বিধি দ্বারা গ্রহণযোগ্য ব্যাখ্যা পাওয়া যায়। আমরা পরে দেখবো যে, যেসব বস্তুর বেগ আলোর বেগের সাথে তুলনীয় নয় তাদের ক্ষেত্রে গ্যালিলিও গ্যালিলিও রূপান্তর বিধি প্রযোজ্য।

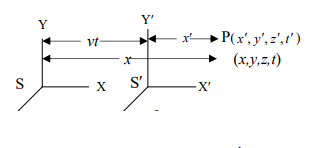
মনে করি, একটি প্রসঙ্গ কাঠামো S এর সাপেক্ষে S’ প্রসঙ্গ কাঠামোটি X-অক্ষ বরাবর । সমবেগে গতিশীল। t = 0 সময়ে S এবং S’ প্রসঙ্গ কাঠামোটির মূল বিন্দু একই অবস্থানে ছিল। P বিন্দুর সংঘটিত কোনো ঘটনার স্থান ও কালাঙ্ক S এর
সাপেক্ষে (x,y,z,t) এবং S’-এর সাপেক্ষে (x’,y’,z’,t’)। t = 1′ সময়ে S’ প্রসঙ্গ কাঠামোটি + X – অক্ষ বরাবর vt দূরে অবস্থান করবে ।

এখন S’ প্রসঙ্গ কাঠামোর পর্যবেক্ষক কর্তৃক পরিমাপকৃত S প্রসঙ্গ কাঠামোর সাপেক্ষে P বিন্দুর স্থানাংক,
x = x’ + vt’

কিন্তু, গ্যালিলিও রূপান্তর বিধি অনুসারে সকল কাঠামোতে সময় অভিন্ন অর্থাৎ t = t’

অতএব, x = x’ + vt …………………….(1)

আবার S প্রসঙ্গ কাঠামোর পর্যবেক্ষক কর্তৃক পরিমাপকৃত S’ প্রসঙ্গ কাঠামোর সাপেক্ষে P বিন্দুর স্থানাংক,

x’=x-vt …………………….(2)

এবং যেহেতু y ও = অক্ষ বরাবর দুই কাঠামোর কোনো আপেক্ষিক বেগ নাই সেহেতু,

y’ = y …………………….(3)

z’ = z …………………….(4)

(1), (2), (3) এবং (4) নং সমীকরণগুলোই গ্যালিলিও রূপান্তর।

এখন সমীকরণগুলোকে সময়ের সাপেক্ষে ব্যবকলন করলে,

dx/dt  = dx’/dt  + v বা, vx = vx’ +v …………………….(5)

dx’/dt  = dx/dt – v  বা, v’x = vx -v …………………….(6)

dy/dt  = dy’/dt      বা, vy = v’y …………………….(7)

dz/dt  = dz’/dt      বা, vz = v’z …………………….(8)

আপেক্ষিক তত্ত্বের দ্বিতীয় স্বীকার্য অনুসারে S ও S’ প্রসঙ্গ কাঠামোর পর্যবেক্ষক কর্তৃক X-অক্ষ বরাবর পরিমাপকৃত আলোর বেগ একই হবে। প্রসঙ্গ কাঠামোর পর্যবেক্ষক কর্তৃক পরিমাপকৃত আলোর বেগ হলে, (5) ও (6) নং সমীকরণে বসালে, c = c’ + v বা, c’ =c-v

সুতরাং, গ্যালিলিও রূপান্তর অনুসারে ঐ বেগ পাওয়া যাবে c’ = c – v অর্থাৎ c’ = c যা আইনস্টাইনের বিশেষ আপেক্ষিক তত্ত্বের দ্বিতীয় স্বীকার্যের পরিপন্থী। কাজেই আপেক্ষিকতার বিশেষ তত্ত্বের দ্বিতীয় স্বীকার্য গ্যালিলিও রূপার বিধি মেনে চলেনা।

সার-সংক্ষেপ :

গ্যালিলিও রূপান্তর বিধিঃ

x=x’ +vt, x’=x-vt, y’ = y, z’ = z

vx = v’x +v, v’x = vx −v, vy =v’y, vz = v’z

বহুনির্বাচনী প্রশ্নঃ

১। গ্যালিলিও রূপান্তর বিধি অনুসারে S এবং S’ কাঠামোর স্থানাঙ্কগুলো হলে যথাক্রমে

ক. x,y,z,t এবং x’,y’,z’, t’

খ. x, y, z,t’ এবং x’, y’,z’, t

গ. x,y,z,t এবং x’, y’, z’, t

ঘ. x’,y’,z’,t’ এবং x,y,z, t

২। আপেক্ষিকতার বিশেষ তত্ত্বের দ্বিতীয় স্বীকার্য গ্যালিলিও রূপান্তর বিধি মেনে চলে না কারণ এই বিধিতে

i. আলোর বেগকে আপেক্ষিক বেগ ধরা হয়েছে।

ii. দুই কাঠামোতেই সময় অপরিবর্তীত ধরা হয়েছে।

iii. দুই কাঠামোতেই নিউটনের সূত্রগুলো সমভাবে প্রযোজ্য ।

নীচের কোনটি সঠিক

ক. i ও ii

খ. ii ও iii

গ. i ও iii

ঘ. i, ii ও iii