আজকে আমাদের আলোচনার বিষয়ঃ চৌম্বক ফ্লাক্স। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৪ তাড়িতচৌম্বক আবেশ ও দিক পরিবর্তী প্রবাহ এর অন্তর্ভুক্ত।
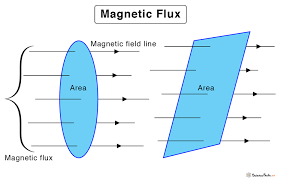
চৌম্বক ফ্লাক্স
একটি চুম্বক বা একটি গতিশীল চার্জের চারপাশে চৌম্বক ক্ষেত্র সৃষ্টি হয়। চৌম্বক ফ্লাক্স, চৌম্বকক্ষেত্র B এর একটি ধর্ম।
চৌম্বক ফ্লাক্স একটি স্কেলার রাশি। চৌম্বক ক্ষেত্রের কোনো তলের ক্ষেত্রফলের সাথে ঐ তলের লম্ব বরাবর চৌম্বক ক্ষেত্রের
উপাংশ গুণ করলে চৌম্বকফ্লাক্স পাওয়া যায়।
তলের ক্ষেত্রফল ভেক্টর ও চৌম্বক ক্ষেত্র ভেক্টর এর স্কেলার গুণফল দ্বারা চৌম্বক ফ্লাক্স পরিমাপ করা হয়।
একে ∅ দ্বারা প্রকাশ করা হয়,
ধরা যাক,
ক্ষেত্রফল ভেক্টর = A
চৌম্বক ক্ষেত্ৰ = B
অন্তর্ভুক্ত কোণ = 8
∅ = A. B= B. A = AB cose
Ā একটি ভেক্টর। এর মান তলের ক্ষেত্রফল এবং দিক হল ঐ তলের লম্ব বরাবর বহির্মুখী।
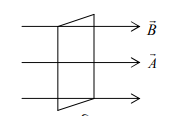
চৌম্বক ক্ষেত্র (B) তলের লম্ব বরাবর হলে (চিত্র)
8 = 0°
∅ = AB
এর একক tesla-m2। একে weber বলা হয়।
চৌম্বকক্ষেত্র রেখা ও চৌম্বক ক্ষেত্র
ক্ষেত্ররেখা বা আবেশরেখার সাথে ফ্লাক্স জড়িত। কোনো স্থান দিয়ে ক্ষেত্ররেখা গমন করলে আমরা বলি, উক্ত স্থান দিয়ে ফ্লাক্স গমন করেছে। ক্ষেত্ররেখার সংখ্যা ফ্লাক্স এর পরিমাণ নির্ধারণ করে। ক্ষেত্ররেখার বাড়ব অস্ত্বিত্ব নেই। কিন্তু ফ্লাক্স পরিমেয়।
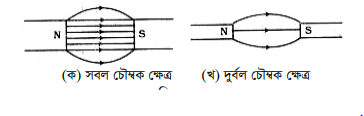
চৌম্বক ক্ষেত্ররেখা বা আবেশ রেখার সন্নিবেশ ঘনত্বের উপর চৌম্বক ক্ষেত্র নির্ভর করে। সন্নিবেশ ঘনত্ব বেশি হলে ক্ষেত্র
সবল, কম হলে ক্ষেত্র দুর্বল।
সুষম চৌম্বক ক্ষেত্রে ক্ষেত্ররেখার সাথে লম্বভাবে অবস্থিত একক ক্ষেত্রফলের মধ্য দিয়ে অতিক্রাড় ক্ষেত্ররেখার সংখ্যার উপর চৌম্বক ক্ষেত্র নির্ভর করে। এ সংখ্যা যত বেশি চৌম্বক ক্ষেত্র তত সবল।
অতএব, ক্ষেত্ররেখার সাহায্যে চৌম্বক ফ্লাক্সের সংজ্ঞা নিম্নরূপে দেয়া যায়:
আবেশরেখা বা ক্ষেত্ররেখার সঙ্গে সংশিণ্টষ্ট যে চৌম্বক রাশির ঘনত্ব দ্বারা চৌম্বক ক্ষেত্র পরিমাপ করা হয় তাকে চৌম্বক ফ্লাক্স বলে ।
চৌম্বক ফ্লাক্স ঘনত্ব:
কোনো সুষম চৌম্বক ক্ষেত্রের সাথে লম্বভাবে অবস্থিত কোন তলের একক ক্ষেত্রফলের মধ্য দিয়ে অতিক্রাড় ফ্লাক্সকে চৌম্বক ফ্লাক্স ঘনত্ব বলে।
একে B দ্বারা প্রকাশ করা হয়। এটি একটি ভেক্টর রাশি। বস্তুত: চৌম্বকফ্লাক্স ঘনত্ব (B) ও চৌম্বক ক্ষেত্র (B) অভিন্ন। যদি A প্রস্থচ্ছেদ বিশিষ্ট একটি কুলী চৌম্বক ক্ষেত্র B এর মধ্যে স্থাপন করা হয়। তাহলে-
চৌম্বক ফ্লাক্স, ∅ = AB cos8.
এখানে, 8 = চৌম্বক ক্ষেত্র এবং কুলীর তলের উপর অঙ্কিত অভিলম্বের মধ্যবর্তী কোণ।
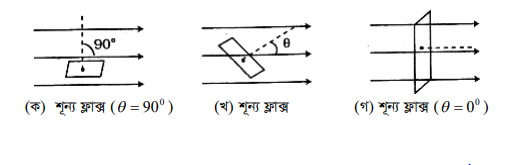
যদি কুলীটি চৌম্বকক্ষেত্রের সমাালে স্থাপন করা হয়,
8 = 90° এবং
∅ = AB cos 90° = 0
যদি কুলীকে চৌম্বকক্ষেত্রের সাথে সমকোণে স্থাপন করা হয় (চিত্র: ৪.৬ গ)
8 = 0°
∅ = AB
B = ∅/A
B এর একক, Wb/m 2 = Wbm-2 বা tesla.
গাণিতিক উদাহরণ:
১. 0.2 m2 ক্ষেত্রফল বিশিষ্ট একটি তল 5×10-5T সুষম চৌম্বকক্ষেত্রের সাথে 30° কোণ তৈরী করে। তলের মধ্য দিয়ে অতিক্রাড় চৌম্বকফ্লাক্স নির্ণয় কর।
এখানে,
A = তলের ক্ষেত্রফল = 0.2m2
B = চৌম্বক ক্ষেত্র = 5×10-5 T
8 = তলের অভিলম্ব ও চৌম্বকক্ষেত্রের মধ্যবর্তী কোণ
= 90°-30° = 60°
আমরা জানি,
∅ = AB cos8
∅ = 0.2m x 5 x 10-5 T cos 60°
∅ = 0.2m2 x 5 x 10-5Tx1/2
= 0.1m2 x 5 x 10-5 T
= 5×10-6 Wb.
উ: 5×10-6 Wb
সার-সংক্ষেপ :
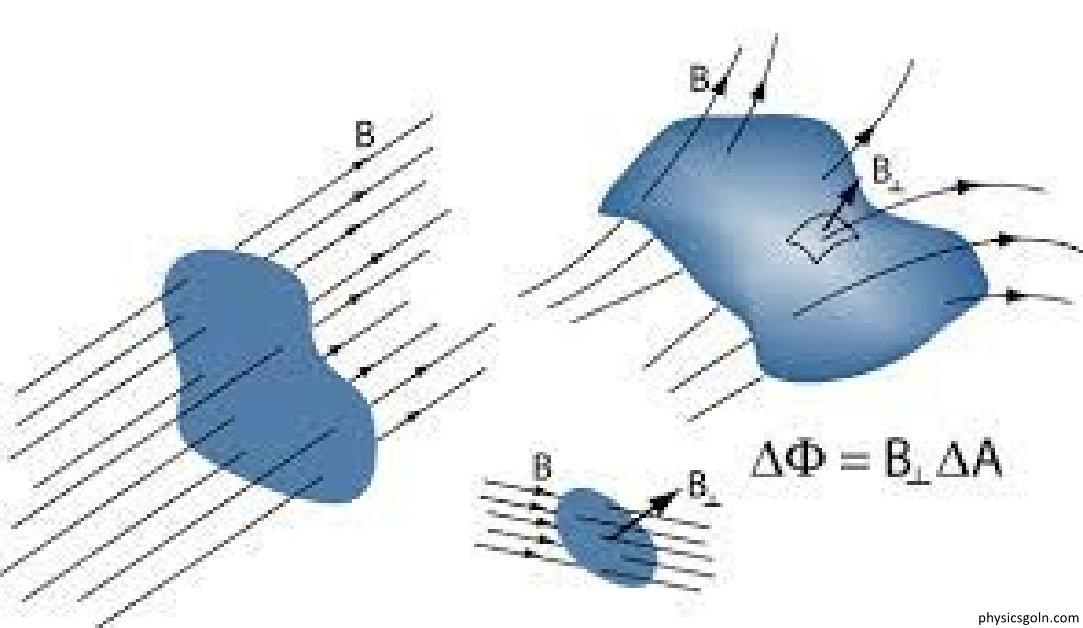
চৌম্বক ফ্লাক্স:
কোনো তলের ক্ষেত্রফল ভেক্টর (Ā) ও চৌম্বক ক্ষেত্র ভেক্টর ( B )-এর স্কেলার গুণফলকে চৌম্বকফ্লাক্স বলা হয়। চৌম্বকফ্লাক্স, p = Ā.B । এর একক weber.
চৌম্বক ফ্লাক্স ঘনত্ব :
কোনো সুষম চৌম্বক ক্ষেত্রের সাথে লম্বভাবে অবস্থিত কোনো তলের একক ক্ষেত্রফলের মধ্য দিয়ে অতিক্রাড় ফ্লাক্সকে চৌম্বক ফ্লাক্সঘনত্ব বলে।
বহুনির্বাচনি প্রশ্ন-
১। যদি এ প্রস্থচ্ছেদ বিশিষ্ট একটি কুলী চৌম্বকক্ষেত্র B এর মধ্যে স্থাপন করা হয় এবং চৌম্বকক্ষেত্র ও কুলীর তলের উপর অঙ্কিত অভিলম্বের মধ্যবর্তী কোণ হয়, তাহলে চৌম্বকফ্লাক্স,
(ক) ∅ = AB sin8
(খ) A/B sin8
(গ) ABcos8
(ঘ) B/A cos8
২। কুলী চৌম্বক ক্ষেত্রের সমাালে থাকলে চৌম্বকফ্লাক্স,
(ক) 0
(খ) A/B
(গ) AB
(ঘ) B/A
৩। যদি কুলীকে চৌম্বকক্ষেত্রের সমকোণে স্থাপন করা হয়,
(ক) ∅ = 0
(খ) ∅ = A/B
(গ) ∅ = AB
(ঘ) B/A
