তরলের প্রকৃত প্রসারাঙ্ক ও আপাত প্রসারাঙ্ক নির্ণয় | পদার্থের উপর তাপের প্রভাব | পদার্থবিজ্ঞান

আপাত প্রসারণ গুণাঙ্ক – পদার্থবিজ্ঞান পদার্থ ও তার গতির বিজ্ঞান। বাংলায় “পদার্থবিজ্ঞান” শব্দটি একটি সমাসবদ্ধ পদ। “পদার্থ” ও “বিজ্ঞান” দুটি সংস্কৃত শব্দ নিয়ে এটি গঠিত। এর ইংরেজি পরিভাষা Physics শব্দটি গ্রিক φύσις (ফুঁসিস) অর্থাৎ “প্রকৃতি”, এবং φυσικῆ (ফুঁসিকে) অর্থাৎ “প্রকৃতি সম্পর্কিত জ্ঞান” থেকে এসেছে। পদার্থবিজ্ঞান বলতে বলা যেতে পারে এটা হলো গণিতের বাস্তব রূপ।

তরলের প্রকৃত প্রসারাঙ্ক ও আপাত প্রসারাঙ্ক নির্ণয় 

১। প্রত্যক্ষ পদ্ধতি (Direct method) : নিম্নলিখিত দুইটি পদ্ধতিতে তরল পদার্থের প্রকৃত প্রসারণ গুণাঙ্ক সরাসরি নির্ণয় করা যায় । এই কারণে উক্ত পদ্ধতি দুইটিকে প্রত্যক্ষ পদ্ধতি বলে ।

(ক) ডুলং ও পেটিট-এর পদ্ধতি (Dulong and Petit’s method) : উদ্ভাবক ডুলং ও পেটিট-এর নাম অনুসারে পদ্ধতিটি ডুলং ও পেটিটের পদ্ধতি নামে পরিচিত। এই যন্ত্রে ABCD একটি দুই মুখ খোলা U-আকৃতির নল, যার AB ও CD বাহুদ্বয় খাড়াভাবে এবং BC নল মানুভূমিকভাবে অবস্থিত। AB ও CD বাহুদ্বয় ঘিরে দু’টি চোঙ এমনভাবে রয়েছে যে, AB ও CD এর উপরের অংশ বের –তে দেখা যায় । প্রত্যেক চোঙে একটি প্রবেশ নল ও একটি নির্গম নল থাকে এবং চোঙের খোলামুখ কর্ক দ্বারা বন্ধ থাকে টি ছাড়া প্রত্যেক চোঙের উপরের কর্কের মধ্য দিয়ে একটি করে থার্মোমিটার প্রবেশ করানো থাকে।

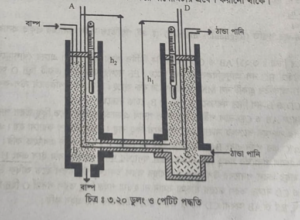
স্তম্ভের উচ্চতা সমান হবে। এরপর AB বেষ্টিত চোঙে বাষ্প এবং CD বেষ্টিত চোঙে ঠান্ডা পানি প্রবাহিত করি। এতে AB বাহুর তরল পদার্থের ঘনত্ব CD বাহুর তরল পদার্থের ঘনত্ব অপেক্ষা কম হবে এবং AB বাহুর তরল পদার্থের উপরিত .CD বাহুর তরল পদার্থের উপরিতল হতে অধিক উচ্চে অবস্থান করবে। উষ্ণ বাহু AB হতে তাপ যাতে BC বাহু দিয়ে CD বাহুতে প্রবাহিত না হয় সেজন্য BC বাহুটি ভিজা ব্লটিং কাগজে জড়ানো থাকে। দুই বাহুর তরল স্তম্ভ দু’টির স্থির অবস্থানে এদের তাপমাত্রা ও উচ্চতার পাঠ গ্রহণ করি। 

হিসাব এবং গণনা ঃ ধরা যাক, ঠান্ডা ও উষ্ণ চোঙের স্থির তাপমাত্রা t°C h°C ও ছ°C তাপমাত্রায় তরল পদার্থের ঘনত্ব যথাক্রমে P ও P2

পরীক্ষাধীন তরল পদার্থের প্রকৃত প্রসারণ গুণাঙ্ক এবং পর্যবেক্ষণ স্থানে অভিকর্ষীয় ত্বরণ ও বায়ুর চাপ যথাক্রমে g ও P তাহলে, আনুভূমিক নলের C বিন্দুতে মোট চাপ = P + hig

ঠান্ডা ও উষ্ণ তরল স্তম্ভের উচ্চতা যথাক্রমে hi ও h2 ও B বিন্দুতে মোট চাপ = P + h2P28 BC আনুভূমিক বলে, C বিন্দুতে মোট চাপ = B বিন্দুতে মোট চাপ’

অর্থাৎ P + h1P1g = P + h228 অথবা, hıP1 = h2P2 (i)

0°C তাপমাত্রায় তরল পদার্থের ঘনত্ব po হলে,

যদি ঠান্ডা চোঙের তাপমাত্রা 0°C এবং উষ্ণ চোঙের তাপমাত্রা t°C হয় এবং উক্ত দুই তাপমাত্রায় তরল স্তম্ভের উচ্চতা যথাক্রমে ho ও h1 হয়, তবে—

hi – họ

Yr= ho xt

(খ) রেনো-এর পদ্ধতি (Regnault’s method) ঃ এই পদ্ধতিতে তরল পদার্থের প্রকৃত প্রসারণ গুণাঙ্ক সঠিকভাবে নির্ণয় করা যায়।

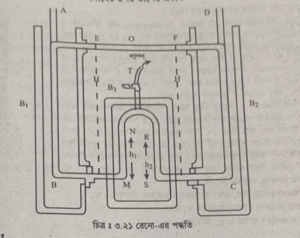
রেনোর যন্ত্রে [চিত্র ঃ ৩.২১] AB ও CD দু’টি লৌহ নির্মিত খাড়া নল আছে। এদের খোলামুখে কিছু নিচে EF নল এবং নিচের প্রান্তদ্বয়ে BC নল আনুভূমিকভাবে যুক্ত আছে। EF নলের মাঝামাঝি একটি ছিদ্র O আছে এবং BC নলের মধ্যভাগে উল্টা U আকৃতির একটি নল MNRS খাড়াভাবে যুক্ত আছে। U নলের উপরিভাগে স্টপ-কর্কযুক্ত একটি পার্শ্ব নল T থাকে। AB, CD ও U-নল ঘিরে যথাক্রমে B1, B2 ও B3 চোঙ রয়েছে।

পরীক্ষা ঃ প্রথমে AB ও CD নলে পরীক্ষাধীন তরল পদার্থ এমনভাবে ঢালি যাতে কিছু তরল পদার্থ ০ ছিদ্র দিয়ে বের হয়ে যায়। অতঃপর সংনমন পাম্পের সাহায্যে T নল দিয়ে কিছু বায়ু U নলে প্রবেশ করানো হয়। এখন B ও B3 চোখে ঘরের তাপমাত্রা 1°C এর পানি এবং B2 চোঙে উচ্চ স্থির তাপমাত্রা °C এর পানি প্রবাহিত করি।

তাপমাত্রার পার্থক্যের দরুন CD নলের তরল পদার্থের ঘনত্ব AB নলের তরল পদার্থের ঘনত্ব অপেক্ষা কম হবে এবং U নলে প্রবিষ্ট অতিরি বায়ুর চাপে MN বাহুর তরল পদার্থের উপরিতল RS বাহুর তরল পদার্থের উপরিতল হতে অধিক উপরে অবস্থান করবে এই অবস্থায় AB ও CD নলের তরল স্তম্ভের উচ্চতা সমান না হওয়া পর্যন্ত কিছু তরল পদার্থ O ছিদ্র দিয়ে বের হয়ে যাবে। পরিশেষে MN, RS ও AB অথবা CD নলের তরল স্তম্ভের উচ্চতার পাঠ গ্রহণ করি।

হিসাব ও গণনা ঃ

ধরা যাক, AB বা CD নলের তরল স্তম্ভের উচ্চতা = H

MN ও RS নলের তরল স্তম্ভের উচ্চতা যথাক্রমে hi ও h2

ti°C ও ছ°C তাপমাত্রায় তরল পদার্থের ঘনত্ব P ও P2

বায়ুমণ্ডলের চাপ = P

U নলের আবদ্ধ বায়ুর চাপ = p

এবং তরল পদার্থের প্রকৃত প্রসারণ গুণাঙ্ক = Y,

যেহেতু নলের BM অংশ আনুভূমিক অতএব B বিন্দুতে চাপ = M বিন্দুতে চাপ অর্থাৎ p + Hp1g = P + hip 1g

.. P – p = (H – hi) pig

.(i)

আবার যেহেতু নলের CS অংশ আনুভূমিক অতএব, C বিন্দুতে চাপ = S বিন্দুতে চাপ অর্থাৎ

p + Hp2g = P + h2pig

:. P – p = (H 2 – h2P1 ) g

..(ii) সমীকরণ (i) ও (ii) অনুসারে P – p = (Hp 2 – h21) g = (H – h1 ) pig

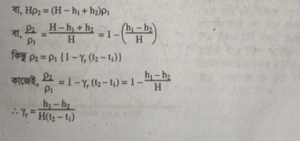
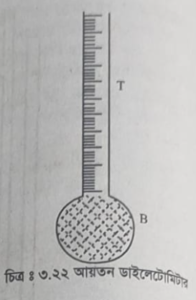
১। আয়তন ডাইলেটোমিটার (Volume dilatometer)-এর সাহায্যে :

আয়তন ডাইলেটোমিটার মূলত একটি কাচের গোলাকার বালব বা কুণ্ড B, যার মুখে ঘনসেন্টিমিটারে দাগাঙ্কিত একটি সরু নল T যুক্ত থাকে। বালব ও নলের কিছু অংশ কোনো তরল দ্বারা ভর্তি করলে ঐ দাগ হতে সরাসরি উক্ত তরলের আয়তন জানা যায়। যে কোনো তাপমাত্রায় বালবের আয়তন নির্ণয় করতে হলে ঐ তাপমাত্রায় যে পরিমাণ পারদ দ্বারা বালটি পূর্ণ হয় তার ওজন জেনে ঐ ওজনকে উক্ত তাপমাত্রার পারদের ঘনত্ব দ্বারা ভাগ করলে ঐ আয়তন পাওয়া যায়।

পরীক্ষা ঃ প্রথমে বাল্‌ব ও নলের কিছু অংশ পরীক্ষাধীন তরলে ভর্তি করে। বালটিকে 0°C তাপমাত্রার বরফে ডুবিয়ে রাখা হয়। এতে তরলের উপরিতল যে দাগে এসে স্থির থাকে তার পাঠ হতে 0°C তাপমাত্রায় আয়তন পাওয়া যায়। এখন ডাইলেটোমিটারের বাল্বটিকে পানিতে ডুবিয়ে রেখে ঐ পানিকে কোনো একটি স্থির তাপমাত্রা ধরা যাক :°C পর্যন্ত উত্তপ্ত করা হয়। এই তাপমাত্রায় তরলের উপরিতল নলের যে দাগে পৌঁছে স্থির থাকে এর পাঠ গ্রহণ করা হয়। এই পাঠ 1°C তাপমাত্রায় তরলের আপাত আয়তন নির্দেশ করে।

হিসাব এবং গণনা ঃ ধরা যাক, O°C তাপমাত্রায় তরলের আয়তন = Vo r°C তাপমাত্রায় তরলের আপাত আয়তন V, এবং নির্ণেয় তরলের প্রসারণ গুণাঙ্ক = Y; তাহলে,

Ya= V-Vo Voxt

বলা বাহুল্য, নলের প্রস্থচ্ছেদ a এবং ঐ দুই তাপমাত্রায় তরলের উপরিতলের মধ্যবর্তী দূরত্ব L হলে V1 – Vo = la –

1.a Voxt Y=

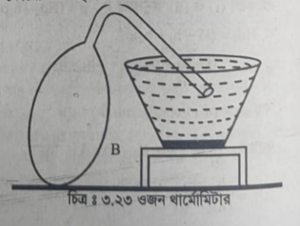
২। ওজন থার্মোমিটার (Weight thermometer)-এর সাহায্যে ঃ ওজন থার্মোমিটার বস্তুত একটি সরু বাঁকা নলযুক্ত কাচের বালব বিশেষ । মনে করি, এটি B । এই নলের প্রান্তভাগে একটি সূক্ষ্ম ছিদ্র আছে। একে বক্র-নলও বলা হয়।

পরীক্ষা ঃ প্রথমে বালবটিকে পরিষ্কার ও শুষ্ক করে খালি অবস্থায় ওজন করি ও ভর বের করি। ধরি, এই ভর W, হল। এরপর থার্মোমিটারের সরু মুখ পরীক্ষাধীন তরল পদার্থে ডুবিয়ে বালবটিকে কয়েকবার পর্যায়ক্রমে গরম ও ঠান্ডা করি। তাপ প্রয়োগে বালবের ভিতরের বায়ু আয়তনে প্রসারিত হয় এবং কিছু বায়ু বের হয়ে যায়। আবার ঠান্ডা করলে থার্মোমিটারের ভিতরস্থ বায়ুর চাপ কমে যায় এবং বাইরের বায়ুর চাপে কিছু তরল পদার্থ বালবে প্রবেশ করে। এভাবে বালবটিকে কয়েকবার পর্যায়ক্রমে গরম ও ঠান্ডা করে থার্মোমিটারটিকে সম্পূর্ণভাবে পরীক্ষাধীন তরল পদার্থ দ্বারা ভর্তি করি। এখন থার্মোমিটারের সরু মুখ পরীক্ষাধীন তরল পদার্থে নিমজ্জিত রেখে এর বালবটিকে একটি পাত্রের সাধারণ পানিতে কিছুক্ষণ ডুবিয়ে রাখি।

বালবটি ঘরের তাপমাত্রা লাভ করলে থার্মোমিটারে ঐ তাপমাত্রা ti°C পড়ে দেখি । অতঃপর থার্মোমিটারটিকে পানি হতে উঠিয়ে এর গা ভালভাবে মুছে পুনরায় ওজন করি। ধরি তরল পদার্থসহ থার্মোমিটারের ভর W হল । এবার থার্মোমিটারের বালবটিকে ফুটন্ত পানিতে অথবা অন্য কোনো উচ্চ স্থির তাপমাত্রার পানিতে ডুবিয়ে রাখি। এতে তরল পদার্থ আয়তনে বৃদ্ধি পায় এবং নল দিয়ে কিছু তরল পদার্থ বের হয়ে যায়। নল দিয়ে বালবের তরল পদার্থ যখন আর বের হয়ে আসতে না দেখা যায় তখন পানির তাপমাত্রা জেনে নিই। ধরি এটি ছ°C এবং ছ > । অতঃপর বালবটিকে পানি হতে উঠিয়ে ঘরের সাধারণ পানি দ্বারা শীতল করি। যখন এর তাপমাত্রা ঘরের তাপমাত্রার সমান হয় তখন এর গা ভালভাবে মুছে জন করি। ধরি, এই ভর W3 হল।

h°C তাপমাত্রায় থার্মোমিটারপূর্ণ তরল পদার্থের ভর = W2 – W1= m, (ধরা যাক) ও ৬°C তাপমাত্রায় থার্মোমিটারপূর্ণ তরল পদার্থের ভর = W3 – W1 = m2 (ধরা যাক)। মনে করি, তরল পদার্থের আপাত প্রসারণ গুণাঙ্ক = Y এবং ti°C ও H°C তাপমাত্রায় তরল পদার্থের ঘনত্ব যথাক্রমে p ও pr

তাহলে, ti°C তাপমাত্রায় m ভরের তরল পদার্থের আয়তন =

Pi

t°C তাপমাত্রায় m2 ভরের তরল পদার্থের আয়তন = m2 P2 কাচ পাত্রের উপাদানের আয়তন প্রসারণ গুণাঙ্ক গ্রাহ্য করলে,

ti°C তাপমাত্রায় m2 ভরের তরল পদার্থের আয়তন = t°C তামপাত্রায় m ভরের তরল পদার্থের আয়তন

অর্থাৎ, m2 m Pi

কাচের আয়তন প্রসারণ গুণাঙ্ক অগ্রাহ্য করবার অর্থই হল তরল পদার্থের প্রকৃত প্রসারণ ও আপাত প্রসারণ সমান পণ্য করা। কাজেই P1 = P2 {1+ Ya (t2 – ti) }

একটি জানা ও অপর একটি অজানা তাপমাত্রায় থার্মোমিটারপূর্ণ তরল পদার্থের ওজন জেনে অজানা তাপমাত্রাটি নির্ণয় করা যায় বলে একে ওজন থার্মোমিটার বলে । 

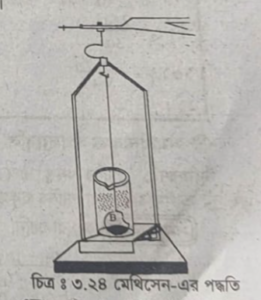
৩। মেথিসেন-এর পদ্ধতির সাহায্যে (By mathiessen’s method) : এই পদ্ধতির কার্যপ্রণালি আর্কিমিডিস-এর নীতির উপর প্রতিষ্ঠিত। এই পদ্ধতিতে প্রায় দুই ইঞ্চি ব্যাসের একটি ছোট কাচের বালব B-এ কিছু [চিত্র ঃ ৩.২৪] ওজন রেখে একে ভারী করা হয় যাতে বালবটি পরীক্ষাধীন তরল পদার্থে সম্পূর্ণ ডুবে যায়। 

পরীক্ষা ঃ প্রথমে একটি সুতার সাহায্যে বালবটিকে উদস্থিতি নিক্তির নিক্তিদণ্ডের এক প্রান্ত হতে ঝুলিয়ে দিয়ে বায়ুতে ওজন করি এবং ভর বের করি। মনে করি, এই ভর m1 গ্রাম হল। এরপর বালবটিকে ঘরের তাপমাত্রায়, মনে করি °C, পরীক্ষাধীন তরল পদার্থে নিমজ্জিত করে পুনরায় ওজন করি। মনে করি, এই ভর m2 গ্রাম হল। এখন বালবটিকে পরীক্ষাধীন তরল পদার্থে ডুবিয়ে রেখে তরল পদার্থকে ধীরে ধীরে উত্তপ্ত করতে থাকি এবং কোনো এক স্থির তাপমাত্রায় ধরা যাক °C-এ বালবটিকে পুনরায় ওজন করি। ধরা যাক, এটি m3 গ্রাম হল ।

হিসাব এবং গণনা ঃ এখানে বালবের বাহ্যিক আয়তন = বালব কর্তৃক

অপসারিত তরল পদার্থের আয়তন। আর্কিমিডিস-এর সূত্র অনুসারে ti°C

তাপমাত্রায় বালব কর্তৃক অপসারিত তরল পদার্থের ভর

=

(m1 – m2) গ্রাম ও

2°C তাপমাত্রায় বালব কর্তৃক অপসারিত তরল পদার্থের ভর (mi – m3) গ্রাম ।

m

ধরা যাক, তরল পদার্থের প্রকৃত ও আপাত প্রসারণ গুণাঙ্ক যথাক্রমে Y1 ও Y এবং ti°C ওt°C তাপমাত্রায় তরল পদার্থের ঘনত্ব যথাক্রমে P ও P2 গ্রাম/ঘনসেমি।

তাহলে, t°C তাপমাত্রায় বালব কর্তৃক অপসারিত তরল পদার্থের আয়তন (m) m2)/p1 ঘন সেমি ও ছ°C াপমাত্রায় বালব কর্তৃক অপসারিত তরল পদার্থের আয়তন = my – ma ঘন সে.মি. ।