দৈর্ঘ্য প্রসারণ গুণাঙ্ক | পদার্থের উপর তাপের প্রভাব | পদার্থবিজ্ঞান

দৈর্ঘ্য প্রসারণ গুণাঙ্ক – পদার্থবিজ্ঞান পদার্থ ও তার গতির বিজ্ঞান। বাংলায় “পদার্থবিজ্ঞান” শব্দটি একটি সমাসবদ্ধ পদ। “পদার্থ” ও “বিজ্ঞান” দুটি সংস্কৃত শব্দ নিয়ে এটি গঠিত। এর ইংরেজি পরিভাষা Physics শব্দটি গ্রিক φύσις (ফুঁসিস) অর্থাৎ “প্রকৃতি”, এবং φυσικῆ (ফুঁসিকে) অর্থাৎ “প্রকৃতি সম্পর্কিত জ্ঞান” থেকে এসেছে। পদার্থবিজ্ঞান বলতে বলা যেতে পারে এটা হলো গণিতের বাস্তব রূপ।

দৈর্ঘ্য প্রসারণ গুণাঙ্ক, ক্ষেত্র প্রসারণ গুণাঙ্ক এবং আয়তন প্রসারণ গুণাঙ্কের এককসমূহের বর্ণনা

কিন্তু t এর একক আছে, সুতরাং দৈর্ঘ্য প্রসারাঙ্ক, ক্ষেত্র প্রসারাঙ্ক ও আয়তন প্রসারাঙ্কের একক : প্রতি ডিগ্রি সেন্টিগ্রেড, অথবা প্রতি ি তাপমাত্রার উপর নির্ভর করে।

কেলভিন (/°C, /°K)। • তিন প্রকার প্রসারণ গুণাঙ্কের মধ্যে সম্পর্ক (Relation between three kinds of co-efficients of expansion) :

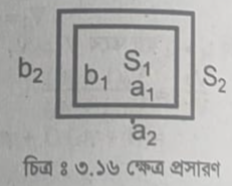
(ক) A ও B এর মধ্যে সম্পর্ক ঃ মনে করি, কোনো এক তাপমাত্রায় একটি বর্গাকার পাতের দৈর্ঘ্য ও প্রস্থ যথাক্রমে

ও b । ঐ তাপমাত্রায় এর ক্ষেত্রফল, S1 = ab |

আবার, মনে করি, t°C তাপমাত্রা বৃদ্ধির ফলে এই পাতের দৈর্ঘ্য ও প্রস্থ বৃদ্ধি যথাক্রমে a ও b2 হয়। যদি পাতের পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্ক ও ক্ষেত্র প্রসারণ গুণাঙ্ক যথাক্রমে ও B হয়, তবে

.. ক্ষেত্রফল, S2 = a2b2 1

a2 = aj (1 + at) …….. (i) b2 = bj (1 + at ) (ii)

এবং S2 = S, (1 + Bt) . (iii) সমীকরণ (i) কে সমীকরণ (ii) দ্বারা গুণ করে,

a2b2 = ajb) (1 + at) 2

বা, S2 = S) (1 + at) 2.

……… (iv) (‘.’ ab = S] এবং a2b2 = $2) সমীকরণ (iii) এবং সমীকরণ (iv) হতে পাই,

S, (1+ẞt) = S, (1 + out)² 1, 1+ẞt=1+2at + a212

বা, 1 + Bt = 1 + 2a [ a এর মান খুব কম তাই এর উচ্চঘাত বর্জনীয় ]

বা, Bt = 2at

অতএব, পদার্থের ক্ষেত্র প্রসারণ গুণাঙ্ক = 2 x দৈর্ঘ্য প্রসারণ গুণাঙ্ক

(খ) a ও Y এর মধ্যে সম্পর্ক :

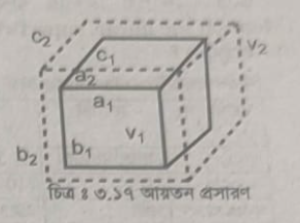
মনে করি, কোনো এক তাপমাত্রায় একটি আয়তাকার পদার্থের দৈর্ঘ্য, গ্রন্থ ও উচ্চতা যথাক্রমে a, b ও c হল।

.. আয়তন, V1 = abc মনে করি, t°C তাপমাত্রা বৃদ্ধির ফলে ঐ আয়তাকার পদার্থের দৈর্ঘ্য, প্রস্থ

ও উচ্চতা বৃদ্ধি পেয়ে a2, b2 ও 2 হল।

 :: আয়তন, V2 = a2 B2C2

যদি আয়তাকার পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্ক ও আয়তন প্রসারণ গুণাঙ্ক

যথাক্রমে x ও y হয়, তবে

a2 = aj (1 + cat).

(vi)

b2 = b1 (1 + out) (vii)

C2 = C1 (1 + act).(viii)

এবং V2 = V1 (T+Yt) (ix)

A সমীকরণ vi, vii ও viii হতে গুণ করে পাই,

a2b2C2 = abıcı (1 + act) 3

বা, V2 = V1 (1 + t) 3.

সমীকরণ (ix) এবং (x) হতে পাই,

V₁ (1+Yt) = V₁ (1 + at)³

বা, 1+yt = (1+ cat 3

=1+3at+3at² + at³

= 1 + 3a t [‘.’ a এর মান খুব কম, তাই উচ্চঘাত বর্জনীয়]

. (x) [‘. V1 = ajbic এবং V2 = a2b

বা, Yt = 3 ot

বা, y = 3a… (xi) অতএব, পদার্থের আয়তন প্রসারণ গুণাঙ্ক = 3 x দৈর্ঘ্য প্রসারণ গুণাঙ্ক

(গ) B ও Y এর মধ্যে সম্পর্ক :

সমীকরণ (v) এবং (xi) হতে লেখা যায়,