আজকে আমরা বিভিন্ন ধরনের নম্বর পদ্ধতি সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ১০ ইলেকট্রনিক্স এর অন্তর্ভুক্ত।
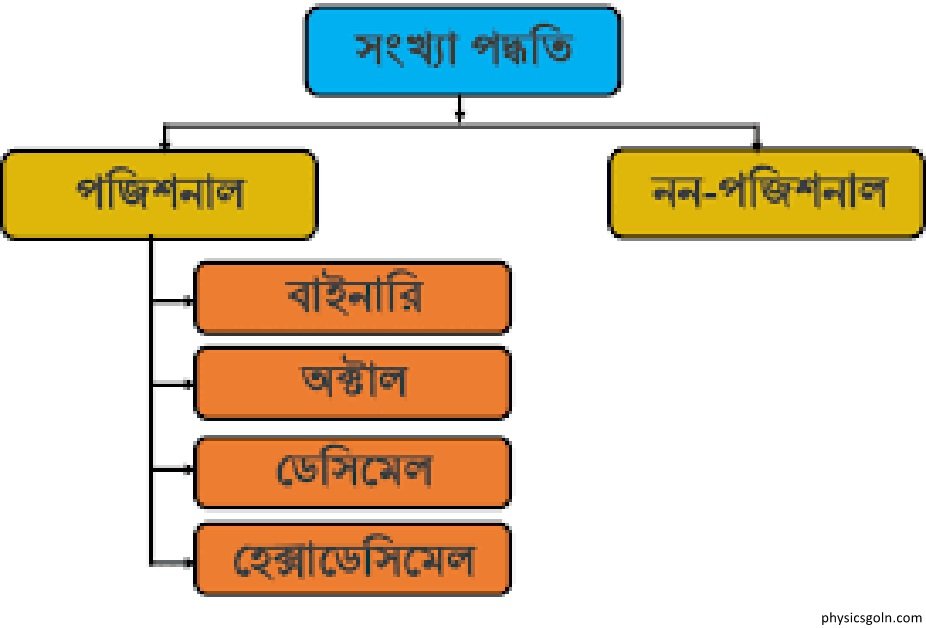
বিভিন্ন ধরনের নম্বর পদ্ধতি
নম্বর পদ্ধতি :
মানব সভ্যতার সূচনালগ্ন থেকেই মানুষ হিসাব বা গণনা করার প্রয়োজনীয়তা অনুভব করে। মূলত তখন থেকেই প্রয়োজনের তাগিদে গণনা করার বিভিন্ন পদ্ধতি উদ্ভাবিত হতে থাকে। হাতের আঙ্গুল, দড়ির গিট, মাটিতে দাগ কাটা ইত্যাদির সাহায্যে মানুষ প্রথম গণনা শুর“ করে। সভ্যতা বিকাশের সাথে সাথে গণনার জন্য মানুষ বিভিন্ন সাংকেতিক চিহ্ন ব্যবহার করতে শুর“ করে।
যেমন : রোমানরা পাঁচ এর জন্য ‘V’ ব্যবহার করত, দশ এর জন্য ‘X’ ব্যবহার করত। এভাবে গণনা বা হিসাবের প্রয়োজনে বিভিন্ন সাংকেতিক চিহ্ন, বর্ণ, সংখ্যা ইত্যাদি প্রচলন শুর— হয়। সাংকেতিক চিহ্নসমূহ ব্যবহার করে কোনো কিছুর পরিমাপ করার কৌশলই হলো গণনা।এই সাংকেতিক চিহ্নসমূহকে নম্বর বা সংখ্যা বলে।
যে পদ্ধতির মাধ্যমে নম্বর বা সংখ্যা লেখা বা প্রকাশ এবং গণনা করা হয় তাকে সংখ্যা বা নম্বর পদ্ধতি বলে।
সংখ্যা পদ্ধতির ভিত
Base of number System
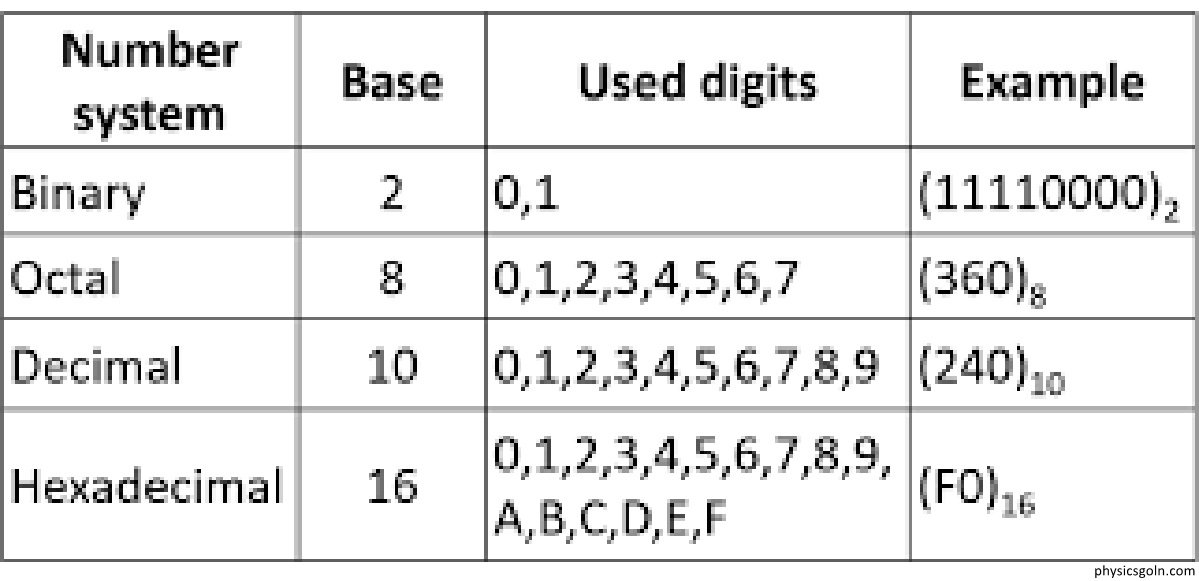
যেকোনো সংখ্যা পদ্ধতিতে ব্যবহৃত মৌলিক চিহ্নসমূহের মোট সংখ্যাকে ঐ সংখ্যা পদ্ধতির ভিত বা বেস বলে। যেমন দশমিক বা ডেসিমেল পদ্ধতিতে দশটি মৌলিক চিহ্ন আছে। এগুলো হলো- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 । সুতরাং এ পদ্ধতির ভিত্তি বা বেস হলো 10। কোনো নম্বর পদ্ধতির ভিত্তি হচ্ছে ঐ পদ্ধতিতে ব্যবহৃত মৌলিক প্রতীক সমূহের মোট সংখ্যা। যেমন – দশমিক পদ্ধতির ভিত্তি হলো 10, কারণ ঐ পদ্ধতিতে দশটি মৌলিক চিহ্ন বা প্রতীক আছে। একই ভাবে বলা যায়, বাইনারি, অক্টাল ও হেক্সাডেসিমেল পদ্ধতিগুলো হলো যথাক্রমে 2 ভিত্তিক, 8 ভিত্তিক ও 16 ভিত্তিক নম্বর পদ্ধতি।
সংখ্যা পদ্ধতির বেস বা ভিতের ওপর নির্ভর করে পজিশনাল সংখ্যা পদ্ধতি বিভিন্ন ধরনের হতে পারে।
স্থানিক সংখ্যা পদ্ধতিতে প্রতিটি সংখ্যায় ব্যবহৃত অঙ্কগুলোর প্রত্যেকটির একটি স্থানিক মান থাকে। এ ধরনের সংখ্যা পদ্ধতি চার ধরনের। যথা –
(১) ডেসিমেল বা দশমিক সংখ্যা পদ্ধতি (Decimal Number System)
(২) বাইনারি সংখ্যা পদ্ধতি (Binary Number System)
(৩) অক্টাল সংখ্যা পদ্ধতি (Octal Number System)
(৪) হেক্সাডেসিমেল সংখ্যা পদ্ধতি (Hexa – Decimal Number System)
নিচে এগুলো সম্পর্কে আলোচনা করা হলো।
১। ডেসিমেল বা দশমিক সংখ্যা পদ্ধতি (Decimal Number System)
আমাদের দৈনন্দিন হিসাব-নিকাশের জন্য বহুল ব্যবহৃত নম্বর পদ্ধতি হলো ডেসিমেল নম্বর বা দশমিক সংখ্যা পদ্ধতি। ডেসিমেল নম্বর পদ্ধতির ভিত্তি (Base) হলো 10। কারণ এই পদ্ধতিতে 10 টি মৌলিক প্রতীক ব্যবহার করা হয়। প্রতীকগুলো হলো 0,1, 2, 3, 4, 5, 6, 7, 8 ও 9। এ পদ্ধতিতে মোট দশটি প্রতীক (অঙ্ক) ব্যবহার করা হয়, বলে এ নম্বর পদ্ধতিকে ডেসিমেল বা দশমিক নম্বর পদ্ধতি বলা হয়।
স্থানীয় মান :
কোনো সংখ্যার প্রতিটি অংকের মান নির্ণয়ের জন্য নিম্নবর্ণিত তথ্য জানা প্রয়োজন ।
(i) অংকটির নিজস্ব মান,
(ii) অংকটির অবস্থান বা স্থানীয় মান
(iii) ঐ নম্বর পদ্ধতির বেস বা ভিত্তি।
ডেসিমেল নম্বর পদ্ধতির একটি সংখ্যা 123.45 বিবেচনা করা যাক। এই সংখ্যাটিতে দশমিকের পূর্বের অংশ পূর্ণমান নির্দেশ করে এবং পরের অংশ ভগ্নাংশ নির্দেশ করে। ডেসিমেল নম্বর পদ্ধতিতে অবস্থানের ওপর অংকের স্থানীয় মান নির্ভর করে। 123.45 সংখ্যাটির স্থানীয় মান নিচে দেখানো হলো:
(123.45)10 = 1×102 + 2×101 + 3×10° + 4×10-1 + 5 × 102
স্থানীয় মান ⇒ 100+20+3+0.4+ 0.05 = (123.45)10
২। বাইনারি সংখ্যা পদ্ধতি (Binary Number System)
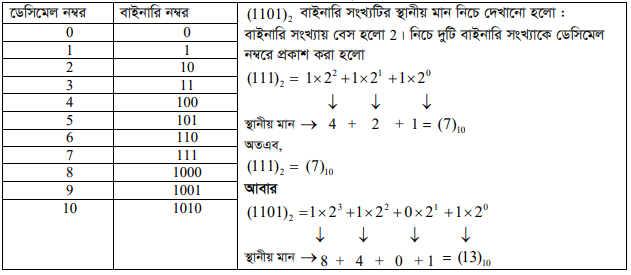
বাই (Bi) মানে দুই। বাইনারি সংখ্যা পদ্ধতিতে 0 এবং 1 এ দুটি অংক ব্যবহার করা হয়। এ সংখ্যা পদ্ধতির ভিত্তি বা বেস হলো 2 । এ পদ্ধতিতে ব্যবহৃত অংক 0 এবং 1 কে Binary Digit বা সংক্ষেপে বিট (Bit) বলে। কম্পিউটারে ডেটা ও তথ্য সংরক্ষণে এবং ডেটা কমিউনিকেশনে বিট মৌলিক একক হিসেবে কাজ করে। আটটি বিটের সমন্বয়ে এক বাইট (Byte) গঠিত হয়।
বাইনারি পদ্ধতিতে এই দুইটি প্রতীক 0 এবং 1 ব্যবহার করে আমরা যেকোনো সংখ্যাকে প্রকাশ করতে পারি, যা ডেসিমেল পদ্ধতিতে 10 টি প্রতীক ব্যবহার করে প্রকাশ করা হয়। বাইনারি পদ্ধতিতে কেবল মাত্র দুই এর বিভিন্ন শক্তি বিশিষ্ঠ পদের সমষ্ঠি দিয়েই নম্বর বা সংখ্যা গঠন করা হয়। ডান থেকে বাম দিকের নম্বরগুলোর স্থানীয় মান যথাক্রমে 29, 21, 23, 23 ইত্যাদি ।
বাইনারি পদ্ধতি হলো সবচেয়ে সরল গণনা পদ্ধতি। তবে বাইনারি গণনায় ডেসিমেল পদ্ধতির তুলনায় বেশি অংকের দরকার হয় বলে সাধারণ ক্ষেত্রে এটির ব্যবহার অসুবিধাজনক। কিন্তু ইলেকট্রনিক যন্ত্রে এক সাথে অনেক বাইনারি অংক দ্বারা দ্র“তগতিতে গাণিতিক ডেটা প্রক্রিয়াকরণ সম্ভব হয়। তাই ইলেকট্রনিক যন্ত্রে বিশেষ করে কম্পিউটারে বাইনারি পদ্ধতি ব্যবহৃত হয়।
নিচের সারণিতে ডেসিমেল নম্বরের সমতুল্য বাইনারি সংখ্যা দেখানো হলো ।
ডেসিমেল ও সমতুল্য বাইনারি সংখ্যা
৩। অকটাল সংখ্যা পদ্ধতি (Octal Number System)
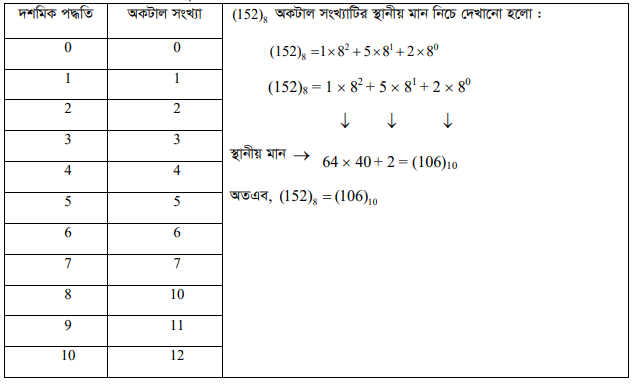
অকটাল সংখ্যা পদ্ধতির ভিত্তি হলো ৪, কেননা এই পদ্ধতিতে ব্যবহৃত মৌলিক প্রতীকের সংখ্যা আটটি। প্রতীকগুলো হলো 0, 1, 2, 3, 4, 5, 6 3 7 । অর্থাৎ অক্টাল নম্বরের যে কোনো ডিজিট 0 হতে 7 পর্যর্ল্ড হতে পারে। আধুনিক কম্পিউটার উন্নয়নের প্রথম দিকে এ পদ্ধতি অত্যন্ড্রু জনপ্রিয় ছিল। সারণিতে অকটাল পদ্ধতির গণনারীতি দেখানো হলো
ডেসিমেল ও সমতুল্য অকটাল সংখ্যা
৪। হেক্সাডেসিমেল সংখ্যা পদ্ধতি (Hexa – Decimal Number System)
হেক্সাডেসিমেল সংখ্যা পদ্ধতির ভিত্তি বা বেস হলো 16 । এই পদ্ধতিতে 16 টি মৌলিক প্রতিক ব্যবহার করা হয়। এগুলো হলো : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E ও F । এখানে 10 হতে 15 ডিজিটগুলোকে A, B, C, D, E ও F দ্বারা বুঝানো হয়েছে। অর্থাৎ A = 10, B = 11, C = 12, D = 13, E = 14, এবং F = 15 ।
হেক্সডিসিমেল নম্বর পদ্ধতি সকল প্রকার কম্পিউটারে ব্যবহার করা হয়।
(20AF)16 হেক্সাডেসিমেল সংখ্যাটির স্থানীয় মান নিচে দেখানো হলো:
(20AF) 16 = 2 × 163+0×162 + 10×161 + 15×160
স্থানীয় মান → 8192+0+160+15 (8367 )10 [ যেহেতু, A = 10, F = 15]
অতএব, (20AF)16 = ( 8367 ) 10
দশমিক ও সমতুল্য হেক্সাডেসিমেল, বাইনারি ও অকটাল সংখ্যা
| দশমিক পদ্ধতি | হেক্সাডেসিমেল সংখ্যা | বাইনারি সংখ্যা | অকটাল সংখ্যা |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 10 | 2 |
| 3 | 3 | 11 | 3 |
| 4 | 4 | 100 | 4 |
| 5 | 5 | 101 | 5 |
| 6 | 6 | 110 | 6 |
| 7 | 7 | 111 | 7 |
| 8 | 8 | 1000 | 10 |
| 9 | 9 | 1001 | 11 |
| 10 | A | 1010 | 12 |
| 11 | B | 1011 | 13 |
| 12 | C | 1100 | 14 |
| 13 | D | 1101 | 15 |
| 14 | E | 1110 | 16 |
| 15 | F | 1111 | 17 |
| 16 | 10 | 10000 | 100 |
| 17 | 11 | 10001 | 101 |
| 18 | 12 | 10010 | 102 |
| 19 | 13 | 10011 | 103 |
| 20 | 14 | 10100 | 104 |
সংখ্যা বা নম্বর পদ্ধতির রূপান্তর
যেকোনো নম্বর পদ্ধতি থেকে ডেসিমেল নম্বর পদ্ধতি থেকে রূপান্তর জন্য অর্থাৎ- বাইনারি, অকটাল, হেক্সাডেসিমেল নম্বর পদ্ধতিতে ডেসিমেল নম্বর পদ্ধতিতে সংখ্যার রূপান্জরের ক্ষেত্রে নিম্নলিখিত ধাপগুলো অনুসরণ করতে হয়। এ ক্ষেত্রে পূর্ণমান এবং ভগ্নাশের জন্য একই নিয়ম প্রযোজ্য ।
নিয়মসমূহ :
(ক) প্রথমে প্রদত্ত সংখ্যাটির ভিত্তি সনাক্ত করে সংখ্যাটির মধ্যে উপস্থিত প্রত্যেকটি অংকের স্থানীয় মান নির্ণয় করতে হবে।
(খ) সংখ্যাটির অর্ভুক্ত প্রত্যেকটি অংকের নিজস্ব মানকে তার স্থানীয় মান দিয়ে গুণ করতে হবে।
(গ) প্রাপ্ত গুণফলগুলোর যোগফলই সমতুল্য দশমিক সংখ্যা হবে।
উদাহরণ :
n ভিত্তিক নম্বর পদ্ধতির কোনো সংখ্যা, যেমন- (538.462 )n কে ডেসিমেল পদ্ধতিতে রূপান্তর :
(538.462)n =5×n²+3×n1 +8×n° +4xn-¹+6×n-²+2×n-³= (?)
ডেসিমেল থেকে বাইনারিতে রূপান্তর
Transformation from Decimal to Binany
(ক) ডেসিমেল পূর্ণ সংখ্যার ক্ষেত্রে
(১) আমরা জানি, বাইনারি সংখ্যার ভিত্তি 2। তাই দশমিক বা ডেসিমেল পূর্ণ সংখ্যাটিকে পর্যায়ক্রমে 2 দ্বারা পূনঃপূন ভাগ
করে যেতে হবে। যতক্ষণ না পর্যন্ত্ ভাগফল শূন্য হয়।
(২) ভাগশেষ বা অবশিষ্ট অংকগুলোকে নিচ থেকে উপরের দিকে সাজালেই বাইনারি সংখ্যা পাওয়া যাবে। নিচের উদাহরণটি লক্ষ করি।
ডেসিমেল সংখ্যা 49 কে বাইনারিতে রূপান্তর :
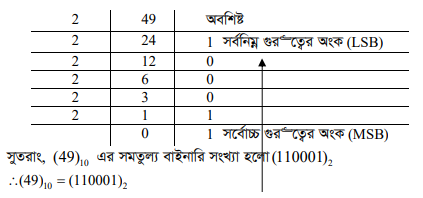
(খ) ডেসিমেল ভগ্নাংশের ক্ষেত্রে –
কোনো ডেসিমেল নম্বরের ভগ্নাংশকে বাইনারি নম্বরে রূপান্ত্র করতে হলে –
(১) ডেসিমেল সংখ্যাটিকে 2 দ্বারা গুণ করতে হবে এবং গুণফল পূর্ণ সংখ্যা না হওয়া পর্যন্ত্ প্রাপ্ত ভগ্নাংশকে 2 দ্বারা গুণ করে যেতে হবে যতক্ষন না ভগ্নাংশ শূন্য হয়। গুণফলের পূর্ণ অংশকে আলাদা করে লিখতে হবে।
(২) যদি গুণফলের পূর্ণ অংশ 1 না থাকে তাহলে ) দ্বারা লিখতে হবে। অতপর প্রতি ক্ষেত্রে প্রাপ্ত গুণফলের পূর্ণ অংশকে উপর থেকে নিচের দিকে পাশাপাশি সাজালেই সমতুল্য বাইনারি সংখ্যা পাওয়া যাবে।
যেমন – 0.375 এর সমতুল্য বাইনারি সংখ্যা হলো – –
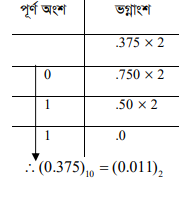
বাইনারি নম্বর থেকে ডেসিমেল নম্বরে রূপান্তর
(১) বাইনারি থেকে ডেসিমেলে রূপান্ডুরের জন্য প্রত্যেকটি ডিজিটের স্থানীয় মানকে 2 এর সূচক হিসেবে লিখতে হবে।
(২) কোনো ডিজিটের ডান পাশে যতটি ডিজিট থাকবে ঐ ডিজিটকে 2 এর তত সূচক দ্বারা গুণ করতে হবে ।
(৩) প্রত্যেকটি ডিজিটকে 2 এর সূচক দ্বারা গুণ করে গুণফলগুলোর যোগফল থেকে সমতুল্য ডেসিমেল সংখ্যা পাওয়া যায় । ভগ্নাংশের ক্ষেত্রে 21, 22, 2-3 ইত্যাদি দ্বারা প্রথম থেকে পরপর গুণ করে গুণফলকে যোগ করে ডেসিমেল ভগ্নাংশ পাওয়া যায়।
উদাহরণ : (101001)2 কে ডেসিমেল সংখ্যায় প্রকাশ ।
(101001)2 = 1 x 25 +0 x 24 + 1 x 2 3 +0×2 2 +0 x 2 +1×2°
= 32 =41 + 0+8+0+0+1
অতএব,
(101001)2-(41)10
ডেসিমেল সংখ্যাকে অকটালে রূপান্তর
(ক) ডেসিমেল পূর্ণ সংখ্যার ক্ষেত্রে –
১। যেহেতু অকটাল সংখ্যার ভিত্তি ৪, তাই ডেসিমেল পূর্ণ সংখ্যাটিকে পর্যায়ক্রমে ৪ দ্বারা ভাগ করতে হবে, যতক্ষণ না ভাগফল শূন্য হয়।
২। তারপর ভাগশেষগুলোকে নিচ থেকে উপরের দিকে পাশাপাশি সাজালেই সমতুল্য অকটাল সংখ্যা পাওয়া যাবে। যেমন – 385 ডেসিমেল সংখ্যাকে অকটালে রূপান্তর-
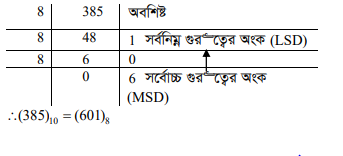
(খ) ডেসিমেল ভগ্নাংশের ক্ষেত্রে –
১। ডেসিমেল ভগ্নাংশ সংখ্যাটিকে ৪ দ্বারা গুণ করতে হবে এবং গুণফল পূর্ণ সংখ্যা না হওয়া পর্যন্ত্ প্রাপ্ত ভগ্নাংশকে ৪ দ্বারা গুণ করে যেতে হবে। গুণফলের পূর্ণ অংশকে আলাদা করে লিখতে হবে।
২। যদি গুণফলের পূর্ণ অংশ 1 থেকে 7 এর মধ্যে না থাকে তাহলে ) দ্বারা লিখতে হবে। অতপর প্রতি ক্ষেত্রে প্রাপ্ত গুণফলের পূর্ণ অংশকে উপর থেকে নিচের দিকে পর্যায়ক্রমে সাজালেই সমতুল্য অকটাল সংখ্যা পাওয়া যাবে।
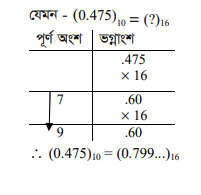
যেমন – (0.475)10 কে অকটালে রূপান্ত্র দেখানো হলো – –
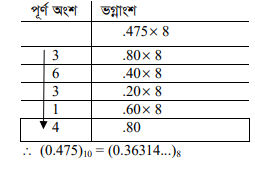
ডেসিমেল সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর
(ক) ডেসিমেল পূর্ণ সংখ্যার ক্ষেত্রে-
১। যেহেতু হেক্সাডেসিমেল সংখ্যার ভিত্তি 16, তাই ডেসিমেল পূর্ণ সংখ্যাকে 16 দ্বারা ভাগ করতে হবে। ভাগফল শূন্য না হওয়া পর্যড় বারবার 16 দ্বারা ভাগ করে যেতে হবে।
২। তারপর ভাগশেষ সংখ্যাগুলোকে নিচ থেকে উপরের দিকে পাশাপাশি সাজালেই সমতুল্য হেক্সাডেসিমেল সংখ্যা
পাওয়া যাবে।
উদাহরণ: (495)10 কে হেক্সাডেসিমেল সংখ্যায় রূপান্তর
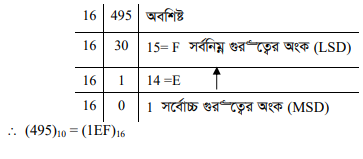
(খ) ডেসিমেল ভগ্নাংশের ক্ষেত্রে –
(১) ডেসিমেল ভগ্নাংশটিকে 16 দ্বারা গুণ করতে হবে এবং গুণফল পূর্ণ সংখ্যা না হওয়া পর্যন্ত্ প্রাপ্ত ভগ্নাংশকে 16 দ্বারা গুণ করে যেতে হবে। গুণফলের পূর্ণ অংশকে আলাদা করে লিখতে হবে।
(২) যদি গুণফলের পূর্ণ অংশ 1 থেকে 15 এর মধ্যে না থাকে তাহলে 0 দ্বারা লিখতে হবে। এরপর প্রতি ক্ষেত্রে প্রাপ্ত গুণফলের পূর্ণ অংশকে উপর থেকে নিচের দিকে সাজালেই সমতুল্য অকটাল সংখ্যা পাওয়া যাবে।
বাইনারি সংখ্যাকে অকটালে রূপান্ডুর
বাইনারি সংখ্যাকে অকটাল সংখ্যায় রূপান্ত্র করতে হলে 0 থেকে 7 পর্যন্ত্ অকটাল নম্বরগুলোর বাইনারি মান মনে রাখলে সুবিধা হবে। নিচের টেবিলে অকটাল নম্বরগুলোর বাইনারি মান দেয়া হলো :
| অকটাল | বাইনারি |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
(ক) বাইনারি পূর্ণ সংখ্যার ক্ষেত্রে – –
১। বাইনারি সংখ্যার ডান দিক থেকে প্রতি তিনটি বিট একত্রে নিয়ে গ্রুপ করে বাম দিকে আসতে হবে এবং বাম দিকের
গ্রপ খালি থাকলে 0 দিয়ে পূর্ণ করতে হবে।
২। এরপর প্রতিটি ভাগকে তার সমতুল্য অকটাল অংক (0 থেকে 7 পর্যন্ত্) দিয়ে নির্দিষ্ট করতে হবে। অংকগুলোকে বাম
থেকে ডানে দিকে সাজালেই অকটাল সংখ্যা পাওয়া যাবে।
যেমন- (11111011)2 কে অকটাল সংখ্যায় রূপান্তর কর।
(খ) বাইনারি ভগ্নাংশের ক্ষেত্রে –
১। বাইনারি সংখ্যার দশমিকের পরে বাম দিক থেকে প্রতি তিনটি বিট একত্রে নিয়ে গ্রুপ করে ডান দিকে আসতে হবে এবং ডান দিকের গ্র“পে খালি থাকলে 0 দিয়ে পূর্ণ করতে হবে।
২। এরপর প্রতিটি গ্রুপকে তার সমতুল্য অকটাল অংক (0 থেকে 7 পর্যন্ত্) দিয়ে প্রকাশ করতে হবে। অংকগুলোকে বাম
থেকে ডানে সাজালেই অকটাল ভগ্নাংশ পাওয়া যাবে।
যেমন – (.1111011)2 কে অকটাল সংখ্যায় রূপান্তর
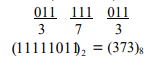
অকটাল নম্বরকে বাইনারি নম্বরে রূপান্তর
(১) অকটাল সংখ্যায় প্রতিটি ডিজিটকে ডান দিক থেকে আলাদা ভাবে তিন ডিজিটের বাইনারিতে পরিবর্তন করতে হবে।
(২) বাইনারি নম্বরগুলোকে একত্রিত করলে অকটাল নম্বরের সমতুল্য বাইনারি নম্বর পাওয়া যাবে।
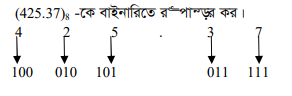
উদাহরণ: (425.37) -কে বাইনারিতে রূপান্তর কর ।
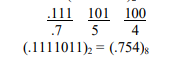
সুতরাং, (425.37)g = (100010101 011111 ) 2
বাইনারি সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপার :
(ক) বাইনারি পূর্ণ সংখ্যার ক্ষেত্রে – –
১। বাইনারি সংখ্যাকে হেক্সাডেসিমেল সংখ্যার রূপা করতে হলে পূর্ণ সংখ্যায় জন্য ডান দিক থেকে বাম দিকে এবং ভগ্নাংশের জন্য বাম দিক হতে ডান দিকে প্রতি চারটি বিট একত্রে নিয়ে গ্রুপ তৈরি করতে হবে। বাম অথবা ডান দিকের গ্র—পে খালি থাকলে ) দিয়ে পূর্ণ করতে হবে।
২। এরপর প্রতিটি গ্রুপকে তার সমতুল্য হেক্সাডেসিমেল অংক (0 থেকে 9 পর্যন্ত্ এবং A, B, C, D, E, F )) দিয়ে প্রকাশ করতে হবে। অংকগুলোকে বাম থেকে ডানে দিকে সাজালেই সমতুল্য হেক্সাডেসিমেল সংখ্যা পাওয়া যাবে।
উদাহরণ- (1111011)2 কে হেক্সাডেসিমেল সংখ্যায় রূপান্তর।
উদাহরণ- (.1111011), কে হেক্সাডেসিমেল সংখ্যায় রূপান্তর
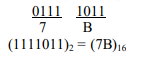
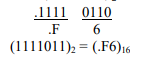
হেক্সাডেসিমেল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর :
(১) হেক্সাডেসিমেল সংখ্যার প্রতিটি ডিজিটকে আলাদাভাবে চার ডিজিটের সমতুল্য বাইনারিতে পরিবর্তন করতে হবে।
(২) বাইনারি নম্বরগুলোকে একত্রিত করলেই হেক্সাডেসিমেল নম্বরের সমতুল্য বাইনারি নম্বর পাওয়া যাবে।
উদাহরণ : (6A.2F) 16 কে বাইনারি সংখ্যায় রূপান্তর

(6A.2E) 16 (0110101000101110)2
অকটাল সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর
ইতোমধ্যে দেখানো হয়েছে যে, হেক্সাডেসিমেল-বাইনারি এবং অকটাল-বাইনারি রূপান্ডুর খুব সহজেই করা যায়।
(১) অকটাল সংখ্যাকে হেক্সডেসিমেল সংখ্যায় রূপারের জন্য প্রথমে সংখ্যাটিকে 3টি করে বাইনারিতে রূপান্তর করতে হবে।
(২) এরপর পূর্ণ নম্বরের ক্ষেত্রে ডান দিক থেকে বাম দিকে এবং ভগ্নাংশের ক্ষেত্রে বাম দিক থেকে প্রতি এটি বিট একত্রে নিয়ে একটি গ্রপ করতে হবে। কোনো কোনো ক্ষেত্রে সর্বশেষ গ্র“পে 4টি বিট নাও থাকতে পারে। সেক্ষেত্রে প্রয়োজনীয় সংখ্যক ( বসাতে হবে।
(৩) প্রতিটি গ্র“পের বাইনারি সমতুল্য হেক্সাডেসিমেল মান লিখতে হবে এবং একত্রিত করতে হবে।
উদাহরণ : (127)g কে হেক্সাডেসিমেলে রূপান্তর :
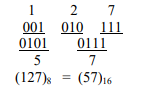
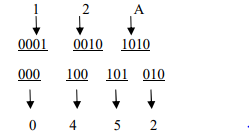
হেক্সাডেসিমেল- অকটাল রূপান্তর : (12A)16 কে অকটালে রূপান্তর কর :
সার-সংক্ষেপ :
যে পদ্ধতির মাধ্যমে নম্বর বা সংখ্যা লেখা বা প্রকাশ এবং গণনা করা হয় তাকে সংখ্যা বা নম্বর পদ্ধতি বলে ।
ডেসিমেল বা দশমিক সংখ্যা পদ্ধতি:
আমাদের দৈনন্দিন হিসাব-নিকাশের জন্য বহুল ব্যবহৃত নম্বর পদ্ধতি হলো ডেসিমেল নম্বর বা দশমিক সংখ্যা পদ্ধতি। ডেসিমেল নম্বর পদ্ধতির ভিত্তি (Base) হলো 10। কারণ এই পদ্ধতিতে 10 টি মৌলিক প্রতীক ব্যবহার করা হয়।
বাইনারি সংখ্যা পদ্ধতি :
বাই (Bi) মানে দুই। বাইনারি সংখ্যা পদ্ধতিতে () এবং 1 এ দুটি অংক ব্যবহার করা হয়।
অকটাল সংখ্যা পদ্ধতি :
অকটাল সংখ্যা পদ্ধতির ভিত্তি হলো ৪, কেননা এই পদ্ধতিতে ব্যবহৃত মৌলিক প্রতীকের সংখ্যা আটটি।
হেক্সাডেসিমেল সংখ্যা পদ্ধতি :
হেক্সাডেসিমেল সংখ্যা পদ্ধতির ভিত্তি বা বেস হলো 16 । এই পদ্ধতিতে 16 টি মৌলিক প্রতিক ব্যবহার করা হয়।
বহুনির্বাচনী প্রশ্ন :
সঠিক উত্তরের পাশে টিক (√) চিহ্ন দিন
১। বাইনারি পদ্ধতিতে লজিক অবস্থা কয়টি?
(ক) একটি
(খ) দু’টি
(গ) তিনটি
(ঘ) চারটি
২। বাইনারি নম্বর ( 10111)2 এর সমতুল্য ডেসিমেল নম্বর কোনটি?
(ক) (22) 10
(খ) (23) 10
(গ) ( 18 ) 10
(ঘ) (30)10
