আজকে আমাদের আলোচনার বিষয়ঃ বিয়োঁ স্যাভাঁর সূত্রের প্রয়োগ। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৩ তড়িৎ প্রবাহের চৌম্বক ক্রিয়া এর অন্তর্ভুক্ত।
বিয়োঁ স্যাভাঁর সূত্রের প্রয়োগ
৩.৩.১ (ক) তড়িৎবাহী লম্বা সোজা পরিবাহী তারের নিকটে কোনো বিন্দুতে B এর মান:
ধরা যাক, শূন্য মাধ্যমে অবস্থিত একটি দীর্ঘ সোজা পরিবাহী তার XY-এর মধ্য দিয়ে I A প্রবাহমাত্রার তড়িৎ প্রবাহিত হচ্ছে।
তার থেকে a লম্ব দূরত্বে অবস্থিত P বিন্দুতে চৌম্বকক্ষেত্র বা চৌম্বক আবেশ B নির্ণয় করতে হবে। তার থেকে a লম্ব দূরত্বে অবস্থিত P একটি বিন্দু [চিত্র: ৩.১০]। স্বল্প দৈর্ঘ্য dl এর জন্য P বিন্দুতে চৌম্বক ক্ষেত্ৰ,
dB = μ0 Idl sin8/4πr2 ………………….. (1)
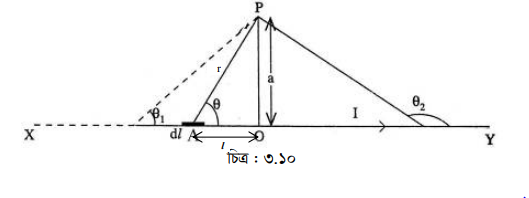
চিত্র থেকে পাই,
OP = a
PA = r
এবং PA তড়িৎ প্রবাহের অভিমুখ XY-এর সাথে ৪ কোণ তৈরি করে ।
r = a/sin8
এবং cot8 = OA/a = -l/a
:: l = -a cot8
যেহেতু, l = acot8
এবং OA = -1 [ :: l হচ্ছে O বিন্দুর বাম দিকে ]
ব্যবকলন করে পাই-
dl = a cosec28d8
১নং সমীকরণে r ও dl-এর মান বসিয়ে পাই,
dB = μ0I(a cosec28d8)sin8/4π (a/sin8d8) 2
বা, dB = μ0I(a cosec28)sin8/4π (a2/cosec28) 2
বা, dB =( μ0I/4πa ).sin8d8
সম্পূর্ণ তারের মধ্য দিয়ে তড়িৎ প্রবাহের জন্য মোট চৌম্বকক্ষেত্র হবে এরকম ক্ষুদ্র ক্ষুদ্র dl-এর জন্য চৌম্বকক্ষেত্রের সমষ্টি। অর্থাৎ,
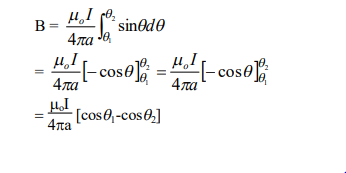
দীর্ঘ লম্বা তারের জন্য তারটি –∝ থেকে +∝ পর্যড্ বিস্তৃত ধরা হয় অর্থাৎ অসীম দৈর্ঘ্য হিসাবে বিবেচিত হয়।
যখন l → – ∝, 81→ 0
এবং যখন l → + ∝, 82→ π
B =( μ0I/4πa) [ cos 0 – cosπ]
= μ0I/2πa
[বিঃ দ্রঃ এক্ষেত্রে, B-এর অভিমুখ হচ্ছে কাগজ পৃষ্ঠের লম্ব বরাবর, নিচ দিকে।
(খ) তড়িৎবাহী বৃত্তাকার পরিবাহীর বা কুলীর কেন্দ্রে B-এর মান :
ধরা যাক, একটি বৃত্তাকার পরিবাহীর মধ্য দিয়ে ঘড়ির গতির বিপরীত দিকে তড়িৎ প্রবাহিত হচ্ছে (চিত্র : ৩.১১)। বৃত্তের ব্যাসার্ধ = r; প্রবাহমাত্রা = I; বিয়োঁ স্যাভোর সূত্রানুসারে ll দৈর্ঘ্যের ক্ষুদ্র অংশের জন্য কেন্দ্র বিন্দু P-তে সৃষ্ট চৌম্বকক্ষেত্র,
dB =(μo/4π)( Idl sine/r2)
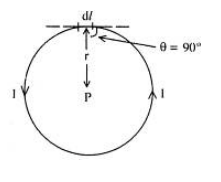
সম্পূর্ণ বৃত্তাকার পরিবাহীকে এরকম ক্ষুদ্র ক্ষুদ্র অংশে বিভক্ত বিবেচনা করা যাক। এসব অংশের ফলে সৃষ্ট চৌম্বকক্ষেত্রের সমষ্টি নিলে সমগ্র কুলীর জন্য এর কেন্দ্রে চৌম্বকক্ষেত্র B-এর মান পাওয়া যাবে।
প্রতিটি অংশ, P বিন্দু থেকে সমান দূরত্বে (r) অবস্থিত; এবং প্রতি অংশ dl, ব্যাসার্ধ r-এর সাথে 90° কোণ তৈরি করে।
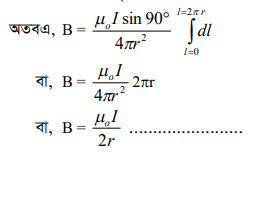
যদি r ব্যাসার্ধবিশিষ্ট N পাকের বৃত্তাকার কুলীর মধ্য দিয়ে I ampere তড়িৎ প্রবাহিত হয় তা হলে সেক্ষেত্রে,
B = μ0NI/2r ………………….. (2)
[বিঃ দ্রঃ এক্ষেত্রে, B -এর দিক হচ্ছে কাগজ পৃষ্ঠের লম্ব বরাবর উপর দিক।]
(গ) দুটি তড়িৎবাহী সমাাল পরিবাহীর মধ্যে ক্রিয়াশীল বল
ধরা যাক, শূন্যস্থানে অবস্থিত RS ও TU লম্বা সোজা সমাাল দুটি পরিবাহী তারে যথাক্রমে I, ও /, তড়িৎ প্রবাহিত হচ্ছে। তারদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব = r [চিত্র]।
ধরা যাক, RS তারের উপর P একটি বিন্দু। TU তারের I, তড়িৎ প্রবাহের জন্য P বিন্দুতে সৃষ্ট চৌম্বকক্ষেত্র,
B = μoI2/2πr
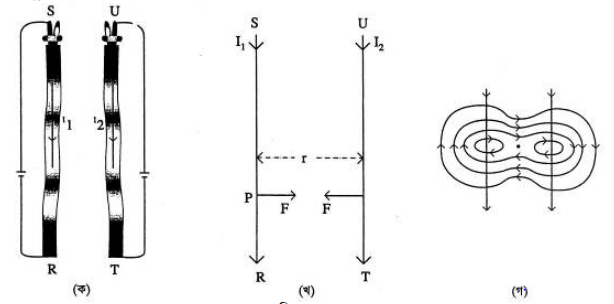
তড়িৎবাহী RS তার উক্ত ক্ষেত্রে অবস্থিত হওয়ায় RS তারের প্রতি একক দৈর্ঘ্যে যে বল ক্রিয়া করবে তার মান, F=BI₁
F = μoI1I2/2πr ………………….. (3)
RS তারের l দৈর্ঘ্যের উপর প্রযুক্ত বল, F = μoI1I2I3/2πr ………………….. (4)
এই বলের অভিমুখ হবে দ্বিতীয় তারের (TU) দিকে ।
I1-এর জন্য TU তারের। দৈর্ঘ্যের উপর প্রযুক্ত বলের মানও একই হবে।
এই বলের অভিমুখ হবে প্রথম তারের (RS) দিকে ।
দুটি সমমুখী সমান্ডুরাল প্রবাহ পরস্পরকে আকর্ষণ করে এবং দুটি বিপরীতমুখী সমাাল প্রবাহ পরস্পরকে বিকর্ষণ করে।
চিত্রে সমমুখী সমাাল প্রবাহের জন্য সমন্বিত চৌম্বক ক্ষেত্রের বলরেখা দেখানো হলো।
যদি I1 = I2 = lA, r = 1 হয়, তাহলে,
F /l = μo/2π = 2×10-7Nm-1
অতএব, তড়িৎ প্রবাহের একক অ্যাম্পিয়ারের সংজ্ঞা নিম্নরূপ:
সংজ্ঞা:
শূন্য মাধ্যমে 1m দূরত্বে অবস্থিত অসীম দৈর্ঘ্যের এবং উপেক্ষণীয় প্রস্থচ্ছেদের দুটি সমাাল সরল পরিবাহীর প্রত্যেকটিতে যে পরিমাণ তড়িৎ প্রবাহ চললে পরস্পরের মধ্যে প্রতি মিটার দৈর্ঘ্যে 2×107 N বল উৎপন্ন হয় তাকে 1 ampere বলে।
[বিঃ দ্রঃ একটি তড়িৎবাহী তার নিজের দ্বারা সৃষ্ট চৌম্বকক্ষেত্রে বল অনুভব করবে না। অন্য কোনো উৎস দ্বারা সৃষ্ট চৌম্বকক্ষেত্রে বল অনুভব করবে।]
গাণিতিক উদাহরণ:
৩.২। একটি লম্বা সোজা তারের মধ্য দিয়ে 4 A. তড়িৎ প্রবাহ চললে উক্ত তার থেকে 0.05 m দূরে চৌম্বক ক্ষেত্র B এর মান নির্ণয় করন। ( u = 4rx 10-7 weber / A m)
আমরা জানি, B = μ0I/2πa
এখানে,
I = তড়িৎ প্রবাহমাত্রা = 4 A
a = লম্ব দূরত্ব = 0.05m = 5x102m
μo= শূন্য মাধ্যমের চৌম্বক প্রবেশ্যতা = 4π ×10-7 weber/A-m
B = (4π ×10-7 × 4) /(2π ×5×10-2) weber/m²
= 1.6×10″ weber/m²
উ: 1.6×10^ weber/m2
৩.৩। একটি তড়িৎবাহী বৃত্তাকার তার কুলীর ব্যাসার্ধ 31.4x10m ও পাক সংখ্যা 400; তারটিতে 5×107A. তড়িৎ প্রবাহিত হলে এর কেন্দ্রে চৌম্বক ফ্লাক্স ঘনত্ব নির্ণয় করন।
আমরা জানি, B = μoNI /2r
এখানে,
শূন্য মাধ্যমের চৌম্বক প্রবেশ্যতা = b = 4rx10-7 weber/A-m
পাক সংখ্যা = N = 400
তড়িৎ প্রবাহ মাত্রা I = 5×107 A
ব্যাসার্ধ = r = 31.4×10m
B = চৌম্বক ফ্লাক্স ঘনত্ব = ?
B = (4π×10-7 × 400 × 5×10-7) /(2×31.4×10-2)
= (4×3.14×400×5×10-12)/(2×31.4)
= 4.0×10-10 weber/m²
উ: 4.0×10-10 weber/m²
৩.৪। দুটি সমাাল তারের মধ্যবর্তী দূরত্ব 0.03m এবং প্রতিটি তারে 120 A. প্রবাহমাত্রা চলছে। যেকোনো একটি তারের 1m দৈর্ঘ্যের উপর ক্রিয়ারত বল নির্ণয় করন।
মনে করি, বল =F
আমরা জানি, এ ক্ষেত্রে,
ক্রিয়াশীল বল, F = μ0I1I2l/2πa
এখানে, μ0 = শূন্য মাধ্যমের চৌম্বক প্রবেশ্যতা = 4π×10-7 weber/A-m
I1 = I2 = তড়িৎ প্রবাহমাত্রা = 120 A
r = দূরত্ব = 0.03m = 3 x10-2 m
l = দৈর্ঘ্য = 1 m.
F = (4π x 10-7 x 120 x 120 x 1)/( 2π ×3×10-2)
= 9600×10-5
= 9.6 × 102N
উ: 9.6×102N.
সার-সংক্ষেপ :
- তড়িৎবাহী লম্বা সোজা পরিবাহী তার থেকে a লম্ব দূরত্বের কোনো বিন্দুতে চৌম্বকক্ষেত্র বা চৌম্বক আবেশ B = μoI/2πr
- তড়িৎবাহী বৃত্তাকার পরিবাহীর কেন্দ্রে B = μ0NI/2r , এখানে N = বৃত্তাকার কুঙ্গুলীর পাক সংখ্যা।
- দুটি লম্বা সোজা সমাাল পরিবাহী তারের মধ্যে ক্রিয়াশীল বল, F = μoI1I2I3/2πr r
এখানে, I ও I2 = পরিবাহী তারের মধ্যে প্রবাহিত তড়িৎ প্রবাহ
r = তার দুটির মধ্যবর্তী দূরত্ব
1 amper- এর সংজ্ঞা: → শূন্য মাধ্যমে 1m দূরত্বে অবস্থিত অসীম দৈর্ঘ্যের এবং উপেক্ষণীয় প্রস্থচ্ছেদের দুটি সমা রাল সরল পরিবাহীর প্রত্যেকটিতে যে পরিমাণ তড়িৎ প্রবাহ চললে পরস্পরের মধ্যে প্রতি মিটার দৈর্ঘ্যে 2×107N বল উৎপন্ন হয় তাকে 1 ampere বলে।
বহু নির্বাচনী প্রশ্ন
সঠিক উত্তরের পাশে টিক (√) চিহ্ন দিন।
১. একটি তড়িৎবাহী লম্বা সোজা পরিবাহী তারের নিকটে কোনো বিন্দুতে B-এর মান,
ক. μ0a/2πI
খ. μ0Ι/ 2πa
গ. μ0Ι/ 4πa
ঘ. 4πa/μ0Ι
২. তড়িৎবাহী বৃত্তাকার পরিবাহীর বা কুটুলীর কেন্দ্রে চৌম্বকক্ষেত্রের মান,
ক. μ0r/2nl
খ. 2μ0r/ 2nl
গ. μ0NI/ 2r
ঘ. μ0nI/4r
৩. শূন্য মাধ্যমে পরস্পর হতে 1m দূরত্বে অবস্থিত খুব দীর্ঘ ও সর— দুটি সমারাল সরল পরিবাহীর প্রত্যেকটিতে 1amp তড়িৎপ্রবাহ চললে পরস্পরের মধ্যে প্রতি মিটার দৈর্ঘ্যে যে বল উৎপন্ন হয় তা হল,
ক. 1×107 N
খ. 1×107 N
গ. 2×10-7 N
ঘ. 2×107 N
