আজকে আমাদের আলোচনার বিষয়ঃ বিয়োঁ স্যাভার সূত্র ও অ্যাম্পিয়ারের সূত্র। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৩ তড়িৎ প্রবাহের চৌম্বক ক্রিয়া এর অন্তর্ভুক্ত।
বিয়োঁ স্যাভার সূত্র ও অ্যাম্পিয়ারের সূত্র
বিয়োঁ স্যাভার সূত্র
কোনো পরিবাহীর মধ্য দিয়ে তড়িৎ প্রবাহ চললে এর চারপাশে কোনো বিন্দুর চৌম্বক ক্ষেত্র B -এর মান বের করার জন্য লাপণ্ডাস একটি সূত্র প্রদান করেন, যা লাপণ্ঢাসের সূত্র নামে পরিচিত। জীন ব্যাপ্টিস্ট বিয়োঁ এবং ফেলিন্স স্যাভা সর্বপ্রথম পরীক্ষার মাধ্যমে লাপন্টাসের সূত্রের সত্যতা প্রমাণ করেন। তাই এ সূত্রটিকে বিয়োঁ স্যাভার এর সূত্রও বলা হয়।
সূত্র :
কোনো পরিবাহীর ক্ষুদ্র দৈর্ঘ্যের মধ্য দিয়ে তড়িৎ প্রবাহিত হলে এর চারপাশে যে চৌম্বকক্ষেত্রের সৃষ্টি হয় তার কোনো বিন্দুতে চৌম্বকক্ষেত্রের মান পরিবাহীর দৈর্ঘ্যের সমানুপাতিক, তড়িৎ প্রবাহের সমানুপাতিক, প্রবাহের দিক এবং পরিবাহীর ঐ অংশের মধ্যবিন্দু ও বিবেচিত বিন্দুর সংযোগ সরলরেখার মধ্যবর্তী কোণের সাইনের সমানুপাতিক এবং দূরত্বের বর্গের ব্যানুপাতিক ।
ব্যাখ্যাঃ
ধরা যাক, CD একটি তড়িৎবাহী তার এবং এর মধ্য দিয়ে I তড়িৎ প্রবাহ চলছে (চিত্র ৩.৮)। এ তড়িৎ প্রবাহের জন্য পরিবাহীর চারপাশে একটি চৌম্বকক্ষেত্রের সৃষ্টি হয়। পরিবাহী তারের যে কোনো ক্ষুদ্র অংশের (dl) তড়িৎ প্রবাহের জন্য সৃষ্ট, যে কোনো P বিন্দুতে, চৌম্বকক্ষেত্রের মান (dB).
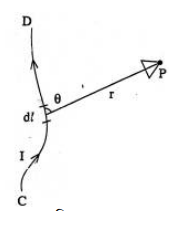
(১) দৈর্ঘ্য dl-এর সমানুপাতিক (dB ∝ dl),
(২) প্রবাহমাত্রা l-এর সমানুপাতিক (dB ∝ l),
(৩) sin8-এর সমানুপাতিক (dB ∝ sin8),
(৪) দূরত্ব r-এর বর্গের ব্যানুপাতিক (dB ∝ sin8 )।
অতএব, প্রবাহখ— Idl-এর জন্য সৃষ্ট P বিন্দুতে চৌম্বকক্ষেত্রের মান,
dB ∝ Idl sin8/r2 …………………………(1)
বা, dB = K. (Idl sin8/r2) …………………………(2)
এখানে, K হচ্ছে সমানুপাতিক ধ্রুবক এবং এর মান I ও r কোন এককে নেয়া হচ্ছে তার উপর এবং মাধ্যমের উপর নির্ভর করে ।
S I পদ্ধতিতে, শূন্য মাধ্যমের ক্ষেত্রে, K = μo/4π
এখানে, μo হচ্ছে শূন্য মাধ্যমের চৌম্বক প্রবেশ্যতা। [μo=4πx10-7 weber/(Am)]
অতএব, (2) নং সমীকরণ হতে,
dB =(μo/4π)( Idl sine/r2) …………………………(3)
(3) নং সমীকরণকে ভেক্টররূপে নিম্ন প্রকারে লেখা যায়:
dB = (μo/4π).I.(dlxr/r3) ………………………..(4)
সম্পূর্ণ তড়িৎবাহী তারের জন্য P বিন্দুতে চৌম্বকক্ষেত্র,
B = ∫dB = (μo/4π)∫(Idlxr/r3)
I ধ্রুব হলে,
B = (μoI/4π)∫(dlxr/r3)
যে কোনো মাধ্যমে,
B = (μI/4π)∫(dlxr/r3) [এখানে, হচ্ছে মাধ্যমটির চৌম্বক প্রবেশ্যতা। ……………………….(4)
[বিঃ দ্রঃ (১) এ সূত্র বাঁকা বা সোজা যে কোনো আকৃতির তারের ক্ষেত্রে প্রযোজ্য ।]
(২) d B-এর অভিমুখ হচ্ছে, dixi ভেক্টরের অভিমুখ বরাবর।
(৩) যে দিকে তড়িৎ প্রবাহিত হয় সে দিকে di-এর অভিমুখ ধরতে হবে ।]
অ্যাম্পিয়ারের সূত্র
স্থির তড়িতে যেমন কুলম্ব সূত্রের সাহায্যে স্থির তড়িৎ ক্ষেত্র সংক্রান্ত্ সহজ সমস্যার সমাধান করা সম্ভব কিন্তু জটিল সমস্যা সমাধানের জন্য গাউস-এর সূত্রের প্রয়োজন হয়। তেমনি তড়িৎ চৌম্বকত্বের ক্ষেত্রে সহজ সমস্যা সমাধানের জন্য বিয়োঁ- স্যাভার সূত্র ব্যবহার করা হয়। কিন্তু জটিল সমস্যা সমাধানের জন্য অ্যাম্পিয়ারের সূত্র প্রয়োগ করা হয়।
সূত্রটি নিম্নরূপ :
“কোনো তড়িৎবাহী পরিবাহীকে কেন্দ্র করে কাল্পনিক কোনো বদ্ধ পথ বরাবর চৌম্বক ক্ষেত্রের রৈখিক সমাকলন, ঐ পরিবাহীর মধ্যে প্রবাহিত প্রবাহমাত্রার to গুণ ।
অর্থাৎ ∮B.dl = μoI
ব্যাখ্যা:
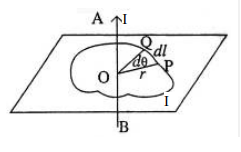
একটি দীর্ঘ সোজা পরিবাহী AB কাগজতলের সাথে লম্বা বরাবর I প্রবাহমাত্রার তড়িৎ প্রবাহিত হচ্ছে। I এর অভিমুখ উপরের দিকে কাগজতলের উপর। একটি বদ্ধ বক্স রেখার উপর একটি ক্ষুদ্র অংশ PQ.
তড়িৎবাহী পরিবাহী AB এর জন্য এই অংশে চুম্বকক্ষেত্র
B = μoI/2πr
:: ∮B.dī = ∮ Bdlcos0° = ∮ Bdl
= μoI/2πr∮dl
PQ অংশের, dl = rd8
:: ∮B.dī = μoI/2πr∮rd8 = μoI/2π = μoI
সার্কিটে মোট প্রবাহমাত্রা = I
:. ∮B.d1 =μoI ……………………….(5)
এটিই-অ্যাম্পিয়ার-এর সূত্র।
গাণিতিক উদাহরণ
১। উত্তর-দক্ষিণ দিক বরাবর স্থাপিত একটি পরিবাহী তারের মধ্য দিয়ে 5A তড়িৎপ্রবাহ প্রবাহিত হচ্ছে দক্ষিণ থেকে উত্তর দিকে। তারের 1cm দৈর্ঘ্য থেকে 45° কোণে উত্তর-পশ্চিম দিকে 1 metre দূরের একটি বিন্দুতে চৌম্বক আবেশ কত হবে?
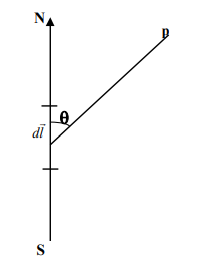
বিয়ো স্যাভার সূত্র অনুসারে P বিন্দুতে চৌম্বক ক্ষেত্রের মান
dB =(μo/4π)( Idl sine/r2)
এখানে, I = 5A, dl=1cm=10-2 m.
r = 1m, 6 = 45°
dB = (4π×10-7)/4π ×(5×10-2 x sin 45°)/ (1)² tesla
= 5 /√2×10-9 tesla
= 3.54×10-9 T.
উ: 3.54×10-9 T.
সার-সংক্ষেপ :
বিয়োঁ স্যাভার সূত্র :
কোনো পরিবাহীর ক্ষুদ্র দৈর্ঘ্যের মধ্য দিয়ে তড়িৎ প্রবাহিত হলে এর চারপাশে যে চৌম্বকক্ষেত্রের সৃষ্টি হয় তার কোনো বিন্দুতে চৌম্বকক্ষেত্রের মান পরিবাহীর দৈর্ঘ্যের সমানুপাতিক, তড়িৎ প্রবাহের সমানুপাতিক, প্রবাহের দিক এবং পরিবাহীর ঐ অংশের মধ্যবিন্দু ও বিবেচিত বিন্দুর সংযোগ সরলরেখার মধ্যবর্তী কোণের সাইনের সমানুপাতিক এবং দূরত্বের বর্গের ব্যানুপাতিক।
অ্যাম্পিয়ারের সূত্র :
কোনো তড়িৎবাহী পরিবাহীকে কেন্দ্র করে কাল্পনিক কোনো বদ্ধপথ বরাবর চৌম্বক ক্ষেত্রের রৈখিক | সমাকলন, ঐ পরিবাহীর মধ্যে প্রবাহিত প্রবাহমাত্রার গুণ। অর্থাৎ, ∮B.dī = μoI
বহু নির্বাচনী প্রশ্ন
সঠিক উত্তরের পাশে টিক (√) চিহ্ন দিন।
১. পরিবাহী তারের ক্ষুদ্র অংশের (dl) তড়িৎ প্রবাহের জন্য সৃষ্ট যে কোনো বিন্দুতে সৃষ্ট চৌম্বক ক্ষেত্রের মান dB
ক. দৈর্ঘ্য dl-এর ব্যানুপাতিক
খ. প্রবাহমাত্রা I-এর সমানুপাতিক
গ. দূরত্ব r-এর সমানুপাতিক
ঘ. sin0-এর ব্যানুপাতিক ।
২. অ্যাম্পিয়ারের সূত্র
ক. ∮B.dī = μo/I
খ. ∮B.dī = I/μo
গ. ∮B.dī = μoI
ঘ. ∮B.dī = 4μI
বহুপদী সমাপ্তিসূচক
পরিবাহী তারের যেকোনো ক্ষুদ্র অংশের (dl) তড়িৎ প্রবাহের জন্য সৃষ্ট, যেকোনো বিন্দুতে, চৌম্বক ক্ষেত্রের মান (dB)
i. দৈর্ঘ্য dl-এর সমানুপাতিক
ii. খ. প্রবাহমাত্রা I-এর সমানুপাতিক
iii. দূরত্ব r-এর বর্গের ব্যড়নুপাতিক।
নিচের কোনটি সঠিক?
ক. i ও ii
খ. ii ও iii
গ. i ও iii
ঘ. ii
