বোরের পরমাণু মডেল

আজকে আমরা বোরের পরমাণু মডেল সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৯ নিউক্লিয় পদার্থবিজ্ঞান এর অন্তর্ভুক্ত।

বোরের পরমাণু মডেল

বিজ্ঞানী নীল্স বোর (Niels Bohr) রাদারফোর্ড পরমাণু মডেলের সাথে পঞ্চাঙ্ক ও আইনস্টাইনের কোয়ান্টাম তত্ত্ব প্রয়োগ করে নতুন এক পরমাণু মডেলের চিত্র উপস্থাপন করেন। এটিই বোরের পরমাণু মডেল নামে পরিচিত। রাদারফোর্ড পরমাণু মডেলের যে বিষয়গুলো নিয়ে কোনো সমস্যা ছিল না সেগুলোকে তিনি অপরিবর্তিত রাখেন। যেমন, রাদারফোর্ড পরমাণু মডেলে পরমাণু অস্থায়ীত্ব এবং অবিচ্ছিন্ন বর্ণালী জনিত সমস্যা সমাধান করতে গিয়ে বোর এমন কিছু যুগাকারী ধারণা উপস্থাপন করেন যা সনাতনী পদার্থবিজ্ঞানের সাথে আদৌ সংগতিপূর্ণ নয় বরং ঘোর বিরোধী। তবুও তৎকালীন পরীক্ষলব্ধ ফলাফলের সাথে বোরের পরমাণু মডেল অনেকটাই সংগতিপূর্ণ হওয়ায় এই মডেলটি বিজ্ঞানীদের কাছে গৃহিত হয় ।

বোরের তত্ত্বের স্বীকার্য (Postulates of Bohr’s Theory) :

বোরের পরমাণু মডেল তিনটি স্বীকার্যের উপর প্রতিষ্ঠিত।

বোরের প্রথম স্বীকার্য:

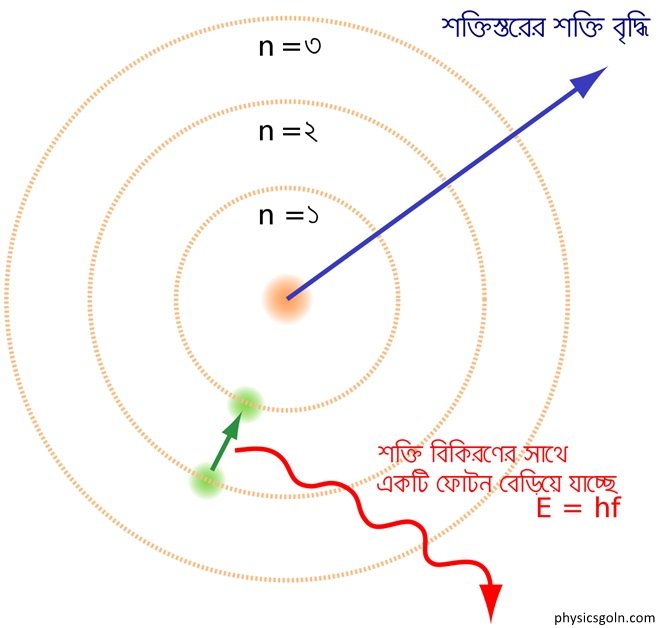
কোনো পরমাণুর ইলেকট্রনগুলো কতকগুলি অনুমোদিত কক্ষপথে বৃত্তাকার পথে আবর্তন করে । অনুমদিত কক্ষপথে আবর্তন কালে ইলেকট্রন কোনো শক্তি বিকিরণ বা শোষণ করেনা। এই অনুমোদিত কক্ষপথগুলোকে স্থায়ী কক্ষপথও বলে।

বোরের দ্বিতীয় স্বীকার্য:

যে কক্ষপথগুলোতে আবর্তনশীল ইলেকট্রনের কৌণিক ভরবেগ h/2π এর অখন্ড গুণিতক সেগুলোই হলো অনুমদিত কক্ষপথ বা স্থায়ী কক্ষপথ। পণ্ডাঙ্কের ধ্রুবক h = 6.63×104Js | দ্বিতীয় স্বীকার্য অনুসারে, কৌণিক ভরবেগ, L = nh/2π …………..(1)

এখানে, n = 1,2,3,4,……. ।

বোরের তৃতীয় স্বীকার্য:

কোনো ইলেকট্রনের এক স্থায়ী কক্ষপথ থেকে অন্য আর এক স্থায়ী কক্ষপথে সংক্রমিত হওয়া সম্ভব। শুধু মাত্র সংক্রমণ কালে তাড়িতচৌম্বক বিকিরণ নিংসৃত বা শোষিত হয়। এই বিকিরণ হলো সমসত্ত্ব এবং এর কম্পাঙ্ক f হলে নিংসৃত বা শোষিত তাড়িতচৌম্বক বিকিরণ hf = E ~ E2 সমীকরণ দিয়ে নির্দেশিত হবে।

একথা সত্য যে, বোরের স্বীকার্যগুলো কোনোটিই সনাতন পদার্থবিজ্ঞানের সাথে সংগতিপূর্ণ নয়। তবুও হাইড্রোজেন সহ কয়েকটি মৌলের পারমাণবিক বর্ণালীর বিশেষণে বোর তত্ত্বের সাফল্য উলেণ্ঢখযোগ্য। এমনকি সামগ্রিকভাবে যেকোনো মৌলের পারমাণবিক গঠন সম্বন্ধে একটি পরিষ্কার চিত্র বোরের পরমাণু তত্ত্ব থেকে পাওয়া যায়। সে কারণে পরীক্ষলব্ধ ফলাফলের সাথে বোর তত্ত্বের কিছু অসংগতি থাকলেও বোর মডেলকেই পারমাণবিক গঠনের ভিত্তি হিসাবে ধরে নেয়া হয় ।

বোর তত্ত্বের প্রয়োগ (Application of Bohr’s Theory) :

১। n – তম অনুমোদিত বা স্থায়ী কক্ষপথের ব্যাসার্ধ (Radius of the n-th Stationary Orbit) :

মনে করি e চার্জ ও m ভরের একটি ইলেকট্রনের n তম অনুমোদিত বা স্থায়ী কক্ষপথে vn বেগে আবর্তন করে এবং এই স্থায়ী কক্ষপথের ব্যাসার্ধ rn।

তাহলে, ইলেকট্রনে n তম স্থায়ী কক্ষপথে কৌণিক ভরবেগ, Ln = mvnrn

দ্বিতীয় স্বীকার্য অনুসারে, mvnrn = nh/2π …………..(2)

এখানে, n = 1,2,3,4,…..

বা, vn = nh/2πmrn …………..(3)

যদি পরমাণবিক সংখ্যা Z হয় তবে নিউক্লিয়াসের চার্জ = Ze

n তম স্থায়ী কক্ষপথে অবস্থিত ইলেকট্রন ও নিউক্লিয়াসের মধ্যে ক্রিয়াশীল কুলম্ব বল,

F = 1/4πεo . (Ze x e/rn2) =  1/4πεo . (Ze²/rn2)

rn ব্যাসার্ধের n তম অনুমোদিত কক্ষ পথে vnবেগে আবর্তনরত ইলেকট্রনের কেন্দ্রবিমুখী বল, F = mvn2/rn

আবার কক্ষপথের স্থিতিশীলতার শর্ত থেকে পাই,

নিউক্লিয়াস ও ইলেকট্রনের মধ্যে আকর্ষণী বল = ইলেকট্রনের আবর্তনজনিত কেন্দ্রবিমুখী বল।

সুতরাং, শর্তানুসারে, 1/4πεo . (Ze x e/rn2) = mvn2/rn

বা, mevn2 = 1/4πεo . (Ze²/rn2)

বা, vn2 = Ze²/4πεo mrn2  …………..(4)

(4) নং সমীকরণে (3) নং সমীকরণের মান বসালে, n2h2/4π2m2rn2 = Ze²/4πεo mrn

বা, rn = εon2h2/π Ze²m …………..(5)

তাহলে, r1 = εoh2/π Ze²m

সুতরাং, rn = n2r1

হাইড্রেজেন পরমাণুর ক্ষেত্রে,  Z = 1

অতএব, rn = εon2h2/πe²m …………..(6)

(6) নং সমীকরণটি হাইড্রোজেন পরমাণুর n তম অনুমোদিত কক্ষপথের ব্যাসার্ধ নির্দেশ করে।

সুতরাং, বলা যায়,  rn ∞ n²…………..(7)

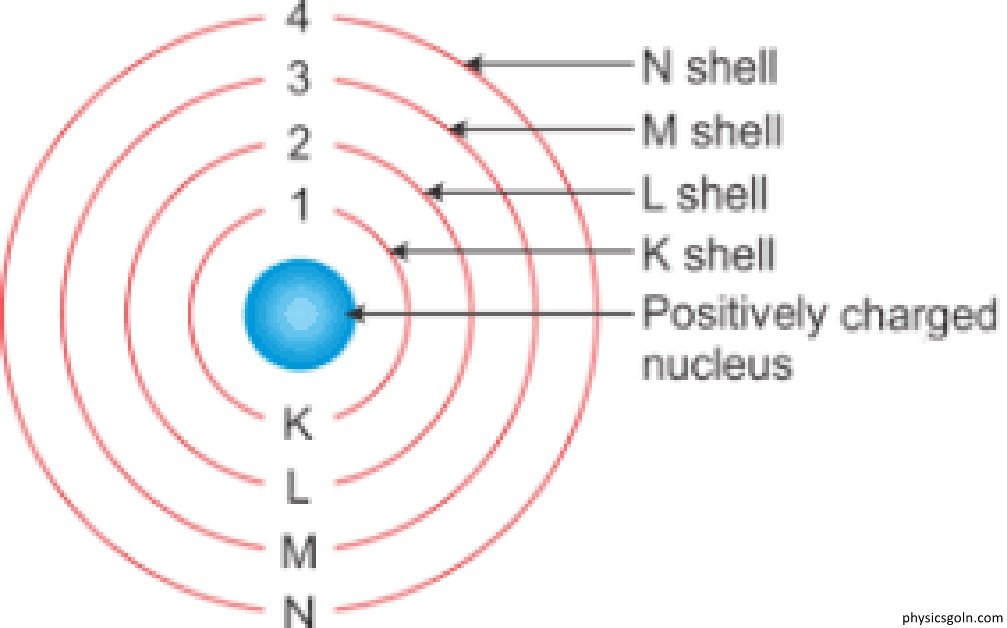
n = 1 বসালে, rn = r1; অর্থাৎ প্রথম অনুমোদিত কক্ষপথের ব্যাসার্ধ। এটাই r -এর ক্ষুদ্রতম মান অর্থাৎ এই কক্ষপথটি নিউক্লিয়াসের সবচেয়ে কাছে অবস্থিত। এই কক্ষপথকে বোরের প্রথম কক্ষপথ বা পরমাণুর K -সেল বলে। বোরের প্রথম কক্ষপথকে ao দিয়ে নির্দেশ করা হয় অর্থাৎ r1 = ao

(6) নং সমীকরণে n = 1 বসালে, ao = εon2h2/πe²m …………..(8)

এখানে,

শূন্য মাধ্যমে ভেদনযোগ্যতা, εo= 8.854 ×10-12 Nm C – 2

পণ্ঢ্যাংকের ধ্রুবক, h = 6.63×10-34 Js

ইলেকট্রনের ভর, m=9.11×103″ kg

ইলেকট্রনের চার্জ, e=1.6×10-C

মান বসালে, ao = {(8.854×10-2)×(6.63×10-34)2}/{ 3.14×(1.6×10-9)×9.11×10-31}

ev, a=0.53×10-10 m = 0.53Å …………..(9)

তাহলে যেকোনো পরমাণুর জন্য ao = (0.53×10-10) /Zm = 0.53/ZÅ

(6) নং সমীকরণের সাথে (8) নং সমীকরণের তুলনা করলে, rn = n²ao …………..(10)

২। n-তম অনুমোদিত বা স্থায়ী কক্ষপথে ইলেকট্রনের বেগ (Velocity of the Electron in n-th Stationary Orbit) :

(3) নং সমীকরণে (5) নং সমীকরণের মান বসালে, vn =  nh/2πme( εon2h2/π Ze²m)

বা, vn = Ze²/2εonh …………..(11)

(11) নং সমীকরণ n – তম অনুমোদিত কক্ষপথে অবস্থিত ইলেকট্রনের বেগ নির্দেশ করে।

তাহলে, r1 = Ze²/2εoh

সুতরাং, rn = r1/n

হাইড্রেজেন পরমাণুর ক্ষেত্রে, Z = 1

অতএব, vn = e²/2εonh …………..(12)

n=1 বসালে, v1 = e²/2εoh

সুতরাং Vn = V1/n

অর্থাৎ প্রথম অনুমোদিত কক্ষপথে অর্থাৎ K- সেলে ইলেকট্রনের বেগ, v1 = e²/2εoh …………..(13)

মান বসালে, V1 = (1.6×10-19) 2/( 2×8.854×10-12 ×6.63×10-34)

বা, vn = 2.2×10^ms -1

(12) নং সমীকরণের সাথে (13) নং সমীকরণের তুলনা করলে,

Vn = V1/n …………..(14)

৩। n– তম অনুমোদিত বা স্থায়ী কক্ষপথে ইলেকট্রনের কৌণিক ভরবেগ(Angular Momemtum of the Electron in – n-th Stationary Orbit) :

বোরের দ্বিতীয় স্বীকার্য অনুসারে, Ln = mvnrn =    nh/2π । এখানে, n = 1,2,3,4,…..

কৌণিক ভরবেগ পরমাণুর পারমাণবিক সংখ্যা Z এর উপর নির্ভরশীল নয়। সুতরাং সকল পরমাণুর ক্ষেত্রেই ইলেকট্রনের কৌণিক ভরবেগ একই ।

তাহলে, L1 = h/2π সুতরাং, L = nL1

সমীকরণ থেকে এটা সুস্পষ্ট যে, Ln ∝ n অর্থাৎ, L1 :L2:L3 =1:2:3 । সুতরাং, অনুমোদিত কক্ষপথ সংখ্যা যত বাড়ে Ln মান তত বাড়ে ।

অর্থাৎ, Ln = nL1 …………..(15)

সুতরাং, L1 = h/2π = (6.63 x 10-34)/( 2 x 3.14 ) = 1.06 ×10- 34 Js

L2 = 2 x h/2π = 2×1.06×10- 34 = 2.12 ×10-34 Js ইত্যাদি।

৪। n-তম অনুমোদিত বা স্থায়ী কক্ষপথে ইলেকট্রনের শক্তি (Energy of the Electron in n-th Stationary Orbit):

n – তম অনুমোদিত বা স্থায়ী কক্ষপথে ইলেকট্রনের গতিশক্তি, Ekn = 1/2mevn2

(11) নং সমীকরণ থেকে vn এর মান বসালে, Ekn = 1/2me(Ze²/2εoh)2

বা, Ekn = 1/2me x (Z2e4/4εo2n2h2)

বা, Ekn = meZ2e4/8εo2n2h2 …………..(16)

n— তম অনুমোদিত বা স্থায়ী কক্ষপথে ইলেকট্রনের বিভব,Vn = 1/4πεo . (Ze/rn)

অতএব, n – তম অনুমোদিত বা স্থায়ী কক্ষপথে ইলেকট্রনের স্থিতিশক্তি, Ep = (-e) Vn

বা, Ep = 1/4πεo . (Ze(-e)/rn)

বা, Ep = 1/4πεo . (Ze2/rn)

(5) নং সমীকরণ থেকে, এর মান বসালে,

rn = εon2h2/π Ze²me

বা, Epn = -1/4πεo . Ze2/(εon2h2/π Ze²me)

বা, Epn = -(meZ2e4/4εo2n2h2) …………..(17)

মোট শক্তি En = Ekn + Epn = meZ2e4/8εo2n2h2 -(meZ2e4/4εo2n2h2)

En = meZ2e4/8εo2n2h2 …………..(18)

এটাই n তম কক্ষ পথের মোট শক্তি। শক্তির ঋন্ত্রক মান প্রমাণ করে যে ইলেকট্রকে পরমাণু থেকে বিচ্ছিন্ন করতে বাহির থেকে শক্তি সরবরাহ করা প্রয়োজন।

n=1 বসালে, E1 = – meZ2e4/8εo2h2

সুতরাং, En = E1/ n2

অর্থাৎ, En ∝ 1/ n2 …………..(19)

হাইড্রোজেন পরমাণুর ক্ষেত্রে, Z = 1

অতএব, En = mee4/8εo2n2h2 …………..(20)

বা, En = mee4/8εo2n2h2 = -e2/{4πεo x 2n2 x (εoh2/πmee2)} = e2/(4πεo x 2n2 x ao) [ao = εoh2/πmee2]

ev, En = -1/4πεo . e2/2n2ao …………..(21)

হাইড্রেজেন পরমাণুর ক্ষেত্রে, প্রথম অনুমোদিত বা স্থায়ী কক্ষপথে ইলেকট্রনের শক্তির ক্ষেত্রে n=1,

AZGE, E1 = -1/4πεo . e2/2ao ………….(22)

(22) নং সমীকরণে ao এবং e এর মান বসালে,

E1 = -9×109 x (1.6×10-19)2/(2×0.53×10-10) = -21.7359×10 J………….(23)

বা, E1 =  21.7359×10-19 /1.6×10-19 eV

বা, E = -13.58eV ≈ -13.6eV  ………….(24)

তাহলে–13.6eV হলো হাইড্রেজেন পরমাণুর প্রথম কক্ষপথের অর্থাৎ ভূমির শক্তি। সুতরাং একটি হাইড্রোজেন পরমাণুকে আয়নিত করতে অর্থাৎ হাইড্রোজেন পরমাণু থেকে ইলেকট্রন মুক্ত করতে বাহির থেকে 13.6eV শক্তি সরবরাহ করতে হবে। একে হাইড্রোজেন পরমাণুর আয়নিত বিভব (ionization potential) বলে ।

আবার, En = -13.6 eV/ n 2

উদাহরণ  ১ ঃ

হাইড্রোজেন পরমাণুর ৩য় কক্ষপথের ব্যাসার্ধ বের করন। এখানে h = 6.63×19-34 js ইলেকট্রনের ভর 9.1×10 kg এবং ইলেকট্রনের চার্জ 1.6 x10-19C

সমাধান ঃ

দেয়া আছে, h = 6.63×19-34 js, m=9.1×10 kg, e=1.6×10-19C, εo = 8.854×10-2C2N1m 2, n = 3

আমার জানি,

হাইড্রজেন পরমাণুর ইলেকট্রনের n তম অনুমোদিত কক্ষপথের ব্যাসার্ধ, rn = εon2h2/πe²me

মান বসালে,rn =(8.854×10-2) ×32 (6.63×19-4)2/ 3.14×9.1×10-31 ×(1.6×10-19)

বা, rn = (8.854 x 6.632×32)/ (3.14×9.1×1.62)×10-11 = 47.86×10-11 = 4.786×10-10 m

বা, rn  = 4.786.4°

উ:4.786 Å

উদাহরণ ২ ঃ

হাইড্রোজেন পরমাণুর দ্বিতীয় কক্ষপথের ইলেকট্রনের শক্তি নির্ণয় কর—ন।

সমাধান :

আমরা জানি, হাইড্রোজেন পরমাণুর n তম কক্ষপথে ইলেকট্রনের শক্তি, En = me4/8n2h2εo2

সুতরাং দ্বিতীয় কক্ষপথে ইলেকট্রনের শক্তি, E2 = – {9.1×10-31 ×(1.6×10-9)4}/{ 8×22 ×(6.63×10-34 ) × 8.85×10-12}

= -5.413×10-19J

E₂ = (-5.413×10-19)/( 1.6×10-19) eV = 3.38eV

উ:3.38eV

উদাহরণ ৩ ঃ

একটি হাইড্রোজের পরমাণুর ভূমি রের শক্তি –13.6eV । একটি ইলেকট্রন প্রথম উত্তেজিত অবস্থা থেকে ভূমিতে ফিরে আসলে কত তরঙ্গদৈর্ঘ্যের ফোটন নির্গত করবে বের করন।

সমাধান ঃ

দেয়া আছে, E1 = −13.6eV প্রথম উত্তেজিত অবস্থার ক্ষেত্রে, n = 2

আমরা জানি, En =  E₁/n2

অতএব, E2 = -13.6eV/ 22 = -3.4eV

তাহলে, ∆E = E2 – E = – 3.4 – ( – 13.6) = 10.2eV= 10.2×1.6×10- J = 16.32×10 J

আবার, ∆E = hv = hc/λ

অতএব, λ = hc/∆E = ( 6.63 x 10- 34 x 3 x 108 )/(16.32×10-19) = 1.21875×107m = 1219Å

উ:1219Å

হাইড্রোজেন বর্ণালীতে বোরের তত্ত্বের ব্যাখ্যা (Spectrum of Hydrogen Explanation on Bohr Theory)ঃ

বোরের তৃতীয় স্বীকার্য থেকে পাই, কোনো ইলেকট্রনের এক উচ্চ স্থায়ী কক্ষপথ m থেকে অন্য আর এক নি স্থায়ী কক্ষপথ n সংক্রমিত হলে সংক্রমণ কালে তড়িৎচৌম্বকীয় বিকিরণ নিংসৃত। এর কম্পাঙ্ক ∫ হলে নিংসৃত তড়িৎচৌম্বকীয় বিকিরণ,
hf = Em – En  ………….(25)

এখানে, Em = m স্থায়ী কক্ষপথের মোট শক্তি এবং En = n স্থায়ী কক্ষপথের মোট শক্তি।

যদি একটি ইলেকট্রন উচ্চ শক্তি m স্থায়ী কক্ষপথ থেকে নি শক্তি n স্থায়ী কক্ষপথে নেমে আসে তবে এই দুই কক্ষ পথের শক্তি ড়রের পার্থক্যের সমান শক্তি নিঃসরণ করবে।

(20) নং সমীকরণ থেকে লেখা যায়, Em = mee4/8εo2m2h2 এবং E = mee4/8εo2n2h2

অতএব, (18) নং সমীকরণে মান বসালে, hf = – mee4/8εo2m2h2 – (- mee4/8εo2n2h2)

বা,  hf = mee4/8εo2h2 (1/n2 – 1/m2)

বা, f = mee4/8εo2h3 (1/n2 – 1/m2) ………….(26)

বা, c/λ = meZ2e4/8εo2h3 (1/n2 – 1/m2)

বা, 1/λ = meZ2e4/8εo2ch3 (1/n2 – 1/m2)

1/λ অর্থাৎ তরঙ্গদৈর্ঘ্যের বিপরীত সংখ্যাকে বলা হয় বিকিরণের কম্পন সংখ্যা (weve number) বা শূন্য স্থানে একক দৈর্ঘ্যে

তরঙ্গ সংখ্যা,

f = 1/λ = f/c এখানে c= আলোর বেগ ।

f = 1/λ = R(1/n2 – 1/m2) ………….(27)

এখান, R = mee4/8εo2h3 = ধ্রুবক ………….(28)

R কে রিডবার্গ ধ্রুবক ( Rydberg Constant) বলে। সমীকরণের ধ্রুবকের সঠিক মানগুলো বসালে,

R=1.09625×10

বোর পরমাণু মডেলের সীমাবদ্ধতা Limitations of Bohr’s Atom moder

বোর পরমাণু মডেলের সীমাবদ্ধতা নিম্নরূপ :

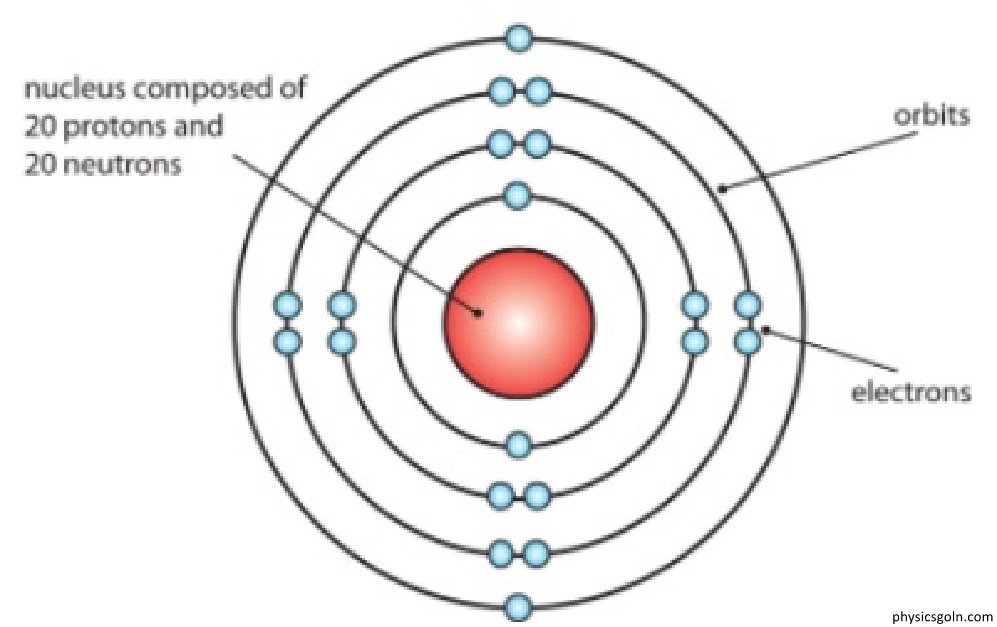
১। বোর পরমাণু মডেল একাধিক ইলেকট্রন বিশিষ্ট পরমাণুসমূহের ব্যাখ্যা করতে পারে না। এ মডেলটি শুধুমাত্র হাইড্রোজেন পরমাণু ও হাইড্রোজেন সদৃশ এক ইলেকট্রনবিশিষ্ট আয়ন (যেমন- Het, Li24) সমূহের বর্ণালী ব্যাখ্যা করতে পারে ।

২। বোর পরমাণু মডেল অনুসারে পরমাণুর অভ্যস্ত্ররে এক শক্তি থেকে অন্য শক্তিস্ত্বরে ইলেক্ট্রনের স্থানান্ত্র ঘটলে, বর্ণালীতে একটি রেখা সৃষ্টি হওয়ার কথা। অধিকতর সূক্ষ্ম বর্ণনালীক্ষণ যন্ত্রের (Spectrometer) সাহায্যে পর্যবেক্ষণ করলে দেখা যায় যে, হাইড্রোজেন ও হাইড্রোজেন সদৃশ অন্যান্য পরমাণুর আয়নের রেখা বর্ণালীতে, প্রতিটি রেখার স্থানে কয়েকটি সূক্ষ্ম রেখা (Fine spectral lines) অবস্থান করছে। বোর মডেল অনুসারে এটি ব্যাখ্যা করা যায় না। এক্ষেত্রে, বিজ্ঞানী সমারফিল্ড (Sommerfeld), ইলেকট্রনের কক্ষপথকে উপবৃত্তাকার কল্পনা করে বর্ণালী রেখার উপর একাধিক সূক্ষ্ম রেখার
অবস্থানের ব্যাখ্যা প্রদান করেন ।

৩। বোর পরমাণু মডেল অনুসারে একটি নির্দিষ্ট কক্ষপথে একই সময়ে ইলেকট্রনের অবস্থান ও ভরবেগ সুনির্দিষ্ট করা হয়েছে। কিন্তু হাইজেনবার্গ অনিশ্চয়তা নীতি (Heigenberg uncertainity principle) অনুসারে একটি নির্দিষ্ট কক্ষপথে অবস্থানরত একটি ইলেকট্রনের অবস্থান ও ভরবেগ একই সময়ে সঠিকভাবে নির্ণয় করা যায় না। সুতরাং বোর পরমাণু মডেল হাইডেনবার্গ অনিশ্চয়তা নীতির পরিপন্থী ।

সার-সংক্ষেপ :

বোরের তত্ত্বের স্বীকার্য :

প্রথম স্বীকার্য:

কোনো পরমাণুর ইলেকট্রনগুলো কতকগুলি অনুমোদিত কক্ষপথে বৃত্তাকার পথে আবর্তন করে। অনুমোদিত কক্ষপথে আবর্তন কালে ইলেকট্রন কোন শক্তি বিকিরণ বা শোষণ করেনা। এই অনুমোদিত কক্ষপথগুলোকে স্থায়ী কক্ষপথও বলে।

 দ্বিতীয় স্বীকার্যঃ

যে কক্ষপথগুলোতে আবর্তনশীল ইলেকট্রনের কৌণিক ভরবেগ h/2π এর অখন্ড গুণিতক সেগুলোই হলো  অনুমোদিত কক্ষপথ বা স্থায়ী কক্ষপথ। পশ্চাঙ্কের ধ্রুবক, h = 6.63×10-34Js ।

বোরের তৃতীয় স্বীকার্য:

কোন ইলেকট্রনের এক স্থায়ী কক্ষপথ থেকে অন্য আর এক স্থায়ী কক্ষপথে সংক্রমিত হওয়া সম্ভব। শুধু মাত্র সংক্রমণ কালে তড়িৎচৌম্বকীয় বিকিরণ নিংসৃত বা শোষিত হয়। এই বিকিরণ হলো সমসত্ত্ব এবং এর কম্পাঙ্ক । হলে নিংসৃত বা শোষিত তড়িৎচৌম্বকীয় বিকিরণ hv = E1 ~ E2 সমীকরণ দিয়ে নির্দেশিত হবে।

বহুনির্বাচনী প্রশ্নঃ

১। বোর তত্ত্বের স্বীকার্য অনুযায়ী-

ক. ইলেকট্রন যে কোনো কক্ষপথে পরিভ্রমন করতে পারে এবং সমড় কক্ষপথেই উহার শক্তি অক্ষুন্ন থাকবে

খ. ইলেকট্রন কতগুলি অনুমোদিত কক্ষপথে আবর্তন করতে পারে এবং সেই সমড় কক্ষপথেই ইলেকট্রনের শক্তি অক্ষুণ্ণ থাকবে

গ. ইলেকট্রন শুধুমাত্র অনুমোদিত কক্ষপথে আবর্তন করবে কিন্তু যেকোনো মানের শক্তির অধিকারী হতে পারবে

ঘ. ইলেকট্রন যে কোনো কক্ষপথে পরিভ্রমন করতে পারে এবং যেকোনো মানের শক্তির অধিকারী হতে পারবে

২। বোরের তত্ত্বানুযায়ী ইলেকট্রন উচ্চ কক্ষপথ থেকে সংক্রমণ করলে তার

ক. স্থিতিশক্তি এবং গতিশক্তি উভয়ই হ্রাস পায়

খ. স্থিতিশক্তি ও মোট শক্তি বৃদ্ধি পায় এবং গতিশক্তি হ্রাস পায়

গ. স্থিতিশক্তি হ্রাস পায় এবং গতিশক্তি বৃদ্ধি পায়

ঘ. স্থিতিশক্তি এবং গতিশক্তি উভয়ই বৃদ্ধি পায়