আজকে আমরা ব্যতিচার ডোরার প্রস্থ সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৭ ভৌত আলোকবিজ্ঞান এর অন্তর্ভুক্ত।
ব্যতিচার ডোরার প্রস্থ
আলোর ব্যতিচারের শর্ত (Condition of Intreference)
4 নং সমীকরণটি নির্দেশ করে যে, লব্ধি তরঙ্গটিও এ তরঙ্গদৈর্ঘ্য বিশিষ্ট তরঙ্গ যার বেগ । কিন্তু 5 নং সমীকরণটি লব্ধি তরঙ্গের বিস্তৃর নির্দেশ করে যা মূল দুটি তরঙ্গের বিস্তৃরের সমান নয় এবং ∆r পথ পার্থক্যের উপর নির্ভর করে। এই ∆r পথ পার্থক্যের উপর নির্ভর করে আমরা গঠনমূলক ব্যতিচার (চরম) এবং ধ্বংসাত্মক ব্যতিচার (অবম) ব্যাখ্যা করা যায়।
গঠনমূলক ব্যতিচারের (চরম বা উজ্জ্বল ডোরার) শর্ত (Condition of Constructive Intreference):
যে সব বিন্দুতে সর্বাধিক প্রাবল্য হবে সেখানেই গঠনমূলক ব্যতিচার হবে অর্থাৎ চরম বা উজ্জ্বল ডোরার পাওয়া যাবে।
সুতরাং, গঠনমূলক ব্যতিচারের ক্ষেত্রে, I, max = 4a2 যখন cos2 π∆r/λ = 1 হবে।
বা, π∆r/λ = 0, π, 2π, 3π ………….হবে
অর্থাৎ π∆r/λ = nπ হবে। এখানে n = 0, 1, 2, 3, 4, …….
বা, ∆r = nπ λ/π
বা, ∆r = nλ (9.20) …………………………(8)
সুতরাং, যেসব বিন্দুতে গঠনমূলক ব্যতিচার গঠিত হবে সেই সব বিন্দুতে তরঙ্গদ্বয়ের পথ পার্থক্যnλ , বিস্তৃর, A = √Imax = ±2a
এবং দশা পার্থক্যকের জন্য (3 নং) সমীকরণে (8 নং) সমীকরণের মান বসালে,
দশা পার্থক্য, ∆δ = 2π/λ x nλ = 2πr
ধ্বংসাত্মক ব্যতিচারের (অবম বা অন্ধকার ডোরার) শর্ত (Condition of Destructive Intreference):
যে সব বিন্দুতে সর্বনি প্রাবল্য হবে সেখানেই ধ্বংসাত্মক ব্যতিচার হবে অর্থাৎ অবম বা অন্ধকার ডোরার পাওয়া যাবে।
সুতরাং ধ্বংসাত্মক ব্যতিচারের ক্ষেত্রে, Imin = 0 যখন cos2π∆r/λ = 0 হবে।
বা, π∆r/λ = π/2, 3π/2, 5π/2 ………….. হবে
অর্থাৎ π∆r/λ = (2n + 1)π/2 । এখানে n = 0,1,2,3,4,……..
বা, ∆r =(2n+1) = π/2 x λ/π
বা, ∆r = ( 2n + 1)λ/2 …………………………(9)
সুতরাং, যেসব বিন্দুতে ধ্বংসাত্মক ব্যতিচার গঠিত হবে সেই সব বিন্দুতে তরঙ্গদ্বয়ের পথ পার্থক্য (2n+1)λ/2, বিস্তৃর, A = √Imins =0
এবং দশা পার্থক্যের জন্য (3 নং) সমীকরণে (9 নং) সমীকরণের মান বসালে,
দশা পার্থক্য, ∆δ = 2π/ λ × (2n+1) λ/2 = (2n + 1)π
ব্যতিচার ঝালরের প্রস্থ (Width of Interference Fringes) :
ইয়াংয়ের দ্বি চিড় পরীক্ষায় উজ্জ্বল ডোরা পাবার শর্ত হলো, ∆r = nλ
এবং অন্ধকার ডোরা পাবার শর্ত হলো, ∆r = (2n+1)/2λ
চিত্রে, S1 ও S2 চিড় দুটি প্রকৃত পক্ষে সুসংহত, সমতরঙ্গ দৈর্ঘ্য সম্পন্ন ও একবর্ণী আলোক উৎস হিসাবে কাজ করে। হাইগেন্সের নীতি অনুসারে S1 ও S2 চিড় দুটি গৌণ উৎস হিসাবে কাজ করবে এবং গৌণ উৎস দুটি হতে সৃষ্ট অণুতরঙ্গগুলো চারিদিকে ছড়িয়ে পরে উৎস এবং পর্দার মধ্যবর্তী অঞ্চলে অগ্রসর হবে।
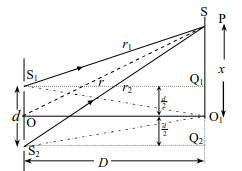
চিত্রে, S হলো পর্দা, d = S1 ও S2 চিড় দুটির মধ্যবর্তী দূরত্ব। এই দূরত্বটি তরঙ্গদৈর্ঘ্য । সাথে তুলনীয়। 0 হলো S ও S, চিড় দুটির মধ্যবিন্দু। OO = D হলো পর্দার দূরত্ব। লক্ষ্যনীয় এই যে, এই দূরত্ব d তুলনায় অত্যন্ড্র বড়, অর্থাৎ D >> d
যেহেতু, S,O, = S,O, সেহেতু উৎস দুটি হতে উৎপন্ন সমদশা সম্পন্ন তরঙ্গ দুটি যাত্রা করে O বিন্দুতে সমদশায় মিলিত হবে। সুতরাং O বিন্দুতে লব্ধি বিার বা তরঙ্গের প্রবল্য সর্বাধিক। একে কেন্দ্রীয় চরম বিন্দু (Central Maximum Point) বলে।
এবার, পর্দার উপর O, বিন্দু থেকে x দূরে P বিন্দু বিবেচনা করা যাক । তাহলে x = OP 1 S1 ও S2 উৎস থেকে দুটি আলোক তরঙ্গ P বিন্দুতে আপতিত হলো। যেহেতু, S, P = 1; এবং S2P = 12 দূরত্বদ্বয় সমান নয় সেহেতু P বিন্দুতে পৌছাতে এদের মধ্যে পথ পার্থক্য ঘটবে। সুতরাং, P বিন্দুটি উজ্জ্বল হবে না অন্ধকার হবে তা নির্ভর করবে তরঙ্গ দুটির পথ পার্থক্যের উপর ।
চিত্রানুসারে,
S₂P² = r2² = D²+ ( x + d/2 ) ²
এবং S1P1 = r1² = D²+( x – d/2 ) ²
অতএব, r2² − r1² = D²+ ( x + d/2 ) ² – D²- ( x – d/2 ) ²
বা, r2² − r1² = ( x + d/2 ) ² – ( x – d/2 ) ² = 4xd/2 2xd
বা, r2 − r1 = 2xd/(r2 + r1)
সুতরাং, পথ পার্থক্য, ∆r = 2xd/(r2 + r1)
যেহেতু, D>> d সেহেতু (r2 + r1) ≈ 2D লেখা যায়।
অতএব, পথ পার্থক্য, ∆r = 2xd/2D = xd/D
সুতরাং, P বিন্দুতে পৌছাতে তরঙ্গ দুটির মধ্যে পথ পার্থক্য,
r2 − r1 = ∆r = xd/D …………………………(10)
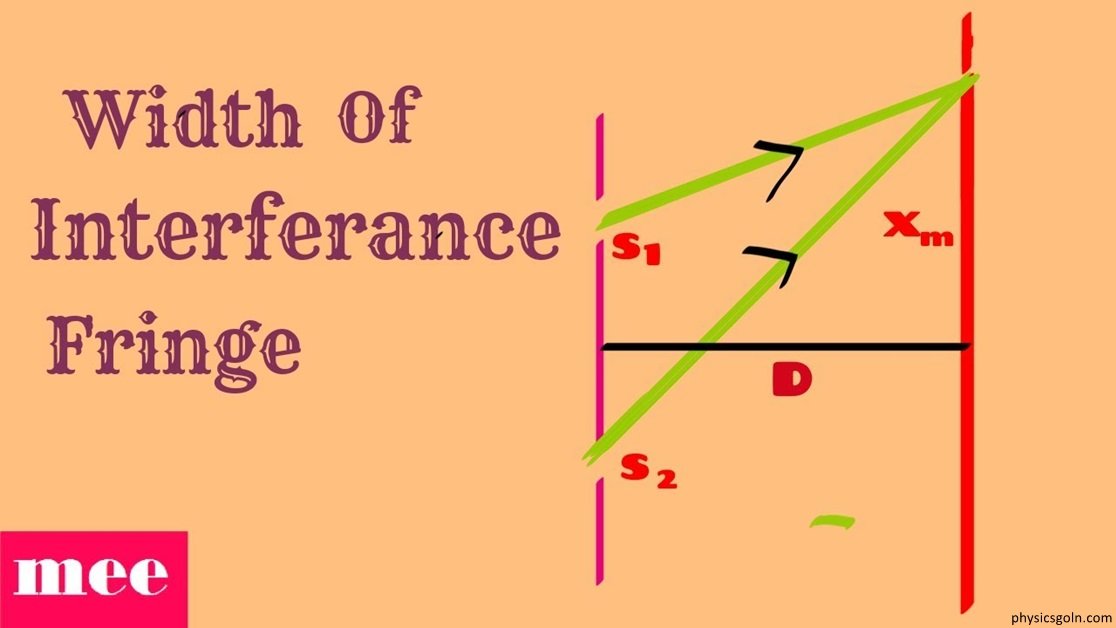
যদি P বিন্দুতে n তম ডোরার সৃষ্টি হয় তবে, x = xn = n তম ডোরার দূরত্ব।
সুতরাং, ∆r = xnd/ D
বা, xn = D/d∆r …………………………(11)
এখন যদি, P বিন্দুতে n তম উজ্জ্বল ডোরার সৃষ্টি হয় তবে, (8 নং) সমীকরণ অনুসারে, ∆r = nλ বসালে,
xn = D/d × nλ
বা, xn = Dnλ/d …………………………(12)
একই ভাবে xn+1 = n+1তম উজ্জ্বল ডোরার দূরত্ব,
xn+1 = D(n+1)λ/d …………………………(13)
তাহলে পরপর দুটি উজ্জ্বল ডোরার মধ্যবর্তী দূরত্ব,
∆x = Xn+1 – Xn = D(n+1)λ/d_Dnλ/d
∆x= Dλ/d ………………………..(14)
এখানে লক্ষ্যণীয় যে পরপর দুটি উজ্জ্বল ডোরার মধ্যবর্তী দূরত্ব কততম ডোরা তার উপর নির্ভর করে না ।
এখন যদি, P বিন্দুতে n তম অন্ধকার ডোরার সৃষ্টি হয় তবে, (9 নং) সমীকরণ অনুসারে, ∆r = (2n+1)λ/2 বসালে,
xn = D/d × (2n+1)λ/2
বা, xn = D(2n+1)λ/2d ………………………..(15)
একই ভাবে Xn+1 = n +1 তম অন্ধকার ডোরার দূরত্বের জন্য n এর স্থলে n + 1 বসালে,
Xn+1 = D[2 (n + 1 ) +1]λ/2d
বা, Xn+1 = D(2n + 3 )λ/2d ……………………….(16)
তাহলে পরপর দুটি অন্ধকার ডোরার মধ্যবর্তী দূরত্ব বা ডোরা ব্যবধান,
∆x = xn+1 – Xn = D(2n+1)λ/2d – D(2n+3)λ/2d
∆x = Ꭰλ/d ……………………….(17)
এখানে লক্ষ্যণীয় যে পরপর দুটি অন্ধকার ডোরার মধ্যবর্তী দূরত্ব কততম ডোরা তার উপর নির্ভর করে না । (14) এবং (17) নং সমীকরণ থেকে বলা যায় যে, পরপর দুটি উজ্জ্বল ডোরা বা পরপর দুটি অন্ধকার ডোরার ব্যবধান সমান। সুতরাং প্রতিটি উজ্জ্বল ডোরার প্রস্থ এবং প্রতিটি অন্ধকার ডোরার প্রস্থ সমান ।
তাহলে, ডোরার প্রস্থকে δx দিয়ে প্রকাশ করলে, প্রতিটি উজ্জ্বল ডোরার বা অন্ধকার ডোরার প্রস্থ,
δx = ∆x/2 = Ꭰλ/2d ……………………….(18)
17 নং সমীকরণ থেকে বলা যায় যে,
(ক) dx এর রাশিমালায় নাই। সুতরাং ডোরা বা ঝালরের প্রস্থ ডোরা সংখ্যার উপর নির্ভর করে না । উজ্জ্বল বা অন্ধকার সব ডোরা প্রস্থ একই।
(খ) ডোরা বা ঝালরের প্রস্থ (δx) তরঙ্গদৈর্ঘ্য (λ) এর সমানুপাতিক। তাই আলোর তরঙ্গদৈর্ঘ্য বড় হলে ডোরা প্রস্থ চওড়া হবে এবং আলোর তরঙ্গদৈর্ঘ্য ছোট হলে ডোরা প্রস্থ চিকন হবে।
(গ) ডোরা বা ঝালরের প্রস্থ (δx) পর্দার দূরত্ব (D) এর সমানুপাতিক। তাই পর্দা দূরে থাকলে ডোরা প্রস্থ চওড়া হবে এবং
পর্দা কাছে থাকলে ডোরা প্রস্থ চিকন হবে।
(ঘ) ডোরা বা ঝালরের প্রস্থ (δx) চিড়ের মধ্যবর্তী দূরত্ব (d)-এর ব্যানুপাতিক। তাই চিড়ের মধ্যবর্তী দূরত্ব যত ছোট হবে ডোরা বা ঝালরের প্রস্থ চওড়া হবে এবং যত বড় হবে ডোরা প্রস্থ চিকন হবে।
(ঙ) শূন্য বা বায়ু মাধ্যম ছাড়া অন্য যেকোনো মাধ্যমে এই পরীক্ষা করলে যেহেতু সেই মাধ্যমের তরঙ্গদৈর্ঘ্য λ’ =λ/μ অর্থাৎ তরঙ্গদৈর্ঘ্য হ্রাস পায় সেহেতু সেই মাধ্যমে ডোরার প্রস্থ শূন্য বা বায়ু মাধ্যম অপেক্ষা কম হবে।
উদাহরণ ১ :
0.4mm পারস্পরিক দূরত্বে অবস্থিত দুটি সমাাল চিড়কে একবর্ণী আলোক রশ্মি দিয়ে আলোকিত করা হলে। চিড় থেকে 40cm দূরে 0.5mm প্রস্থের ঝালর গঠিত হয়। আলার তরঙ্গদৈর্ঘ্য নির্ণয় করন।
সমাধান:
দেয়া আছে, d = 0.4 mm = 4 ×10^-4m, D = 40 cm = 0.4m, ∆x = 0.5mm = 5×10-4 m এবং λ = ?
আমরা জানি, ঝালরের প্রস্থ ∆x= Dλ/d
বা, λ = d∆x/D
মান বসালে, A = 4×10-4 × 5×10-4/ 0.4 = 5×10-7 = 5000 Å
উ: 5000 Å
উদাহরণ ২ :
একটি দ্বি-চিড়ের চিড়দ্বয়ের মধ্যবর্তী দূরত্ব 0.5 mm । এই চিড়দ্বয়কে 4800 Å তরঙ্গদৈর্ঘ্যের আলোতে আলোকিত করা হলো । চিড় থেকে কত দূরে পর্দা রাখলে ঝালরের বেধ 1mm হবে?
সমাধান:
দেয়া আছে, d=0.5m=5×10-4 m, λ=4800 Å = 4800×10-10 m, D = 40cm = 0.4m, δx = 0.2 mm = 2×10-4 m এবং D=?
আমরা জানি,
ঝালরের বেধ δx = Dλ/2d.
বা, D = 2dδx/ λ
মান বসালে, D = (2 x 5 x 10-4 x 2 x 10-4)/(4800 × 10-10) = 0.417m = 41.7cm
উ: 41.7cm
উদাহরণ ৩ :
0.2mm ব্যবধান বিশিষ্ট দুটি চিড় হতে 50cm দূরত্বে অবস্থিত পর্দার উপর ব্যতিচার সৃষ্টি করা হল। পরপর দুটি উজ্জ্বল পট্টির মধ্যবর্তী দূরত্ব 1.42mm হলে আলোর তরঙ্গদৈর্ঘ্য নির্ণয় করন।
সমাধান :
দেয়া আছে, d = 0.2mm = 2×10-4 m, D = 50 cm = 0.5m, ∆x = 1.42mm = 1.42 x10-3 m এবং λ = ?
আমরা জানি,
ডোরার প্রস্থ, ∆x = λD/d
বা λ = d∆x/D
মান বসালে, λ = (2×10-4 ×1.42×10-3)/ 0.5 = 5.68 x 10-7m = 5680Å
উ: 5680 Å
সার-সংক্ষেপ :
গঠনমূলক ব্যাতিচার (চরম বা উজ্জ্বল ডোরার):
যে সব বিন্দুতে সর্বাধিক প্রাবল্য হবে সেখানেই গঠনমূলক ব্যাতিচার হবে অর্থাৎ চরম বা উজ্জ্বল ডোরা পাওয়া যাবে।
ধ্বংসাত্মক ব্যাতিচার (অবম বা অন্ধকার ডোরার ):
যে সব বিন্দুতে সর্বনি প্রাবল্য হবে সেখানেই ধ্বংসাত্মক ব্যাতিচার হবে অর্থাৎ অবম বা অন্ধকার ডোরা পাওয়া যাবে।
পরপর দুটি উজ্জ্বল বা অন্ধকার ডোরার মধ্যবর্তী দূরত্ব, ∆x = λD/d
প্রতিটি উজ্জ্বল ডোরা বা প্রতিটি অন্ধকার ডোরার প্রস্থ, δx = Δx/2 = λD/2d
বহুনির্বাচনী প্রশ্নঃ
১। ধ্বংসাত্মক ব্যতিচারে অন্ধকার ডোরা সৃষ্টির কারণ ঐ স্থানে
i. তরঙ্গ দুটি বিপরীত দশায় মিলিত হয়।
ii. তরঙ্গ দুটির মধ্যে পথ পার্থক্য λ/2 এর অযুগ্ম গুণিতক হয়।
iii. তরঙ্গ দুটির মধ্যে দশা পার্থক্য । এর অযুগ্ম গুণিতক হয়।
কোনটি সঠিক?
ক. i ও ii
খ. ii ও iii
গ. i iii
ঘ. i, ii ও iii
কোনটি সঠিক?
ক. i ও ii
খ. ii ও iii
গ. i 3 iii
ঘ. i, ii ও iii
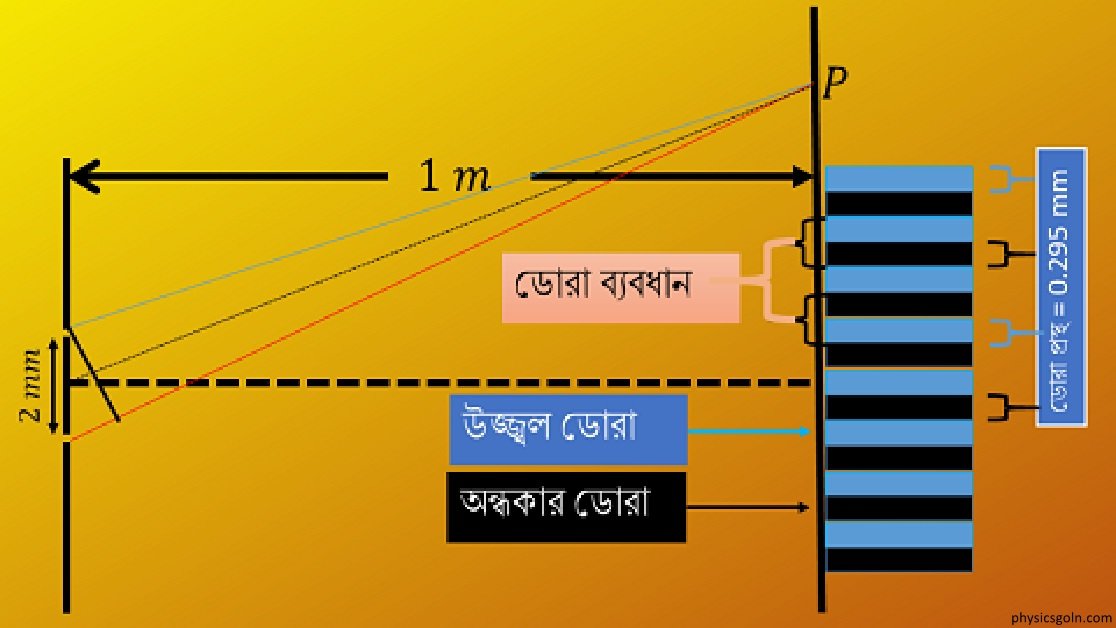
২। 0.4 mm ব্যবধান বিশিষ্ট দুটি চিড় হতে 1m দূরে অবস্থিত পর্দার উপর ব্যতিচার সজ্জা সৃষ্টি হলো। ব্যবহৃত আলোর তরঙ্গদৈর্ঘ্য 50004 হলে পর পর দুটি উজ্জ্বল ও অন্ধকার পট্টির কেন্দ্রের মধ্যবর্তী দূরত্ব কত?
ক. 125 mm
খ. 1.25 mm
গ. 1.25 mm
ঘ. 1.50 mm
