ভরের আপেক্ষিকতা : ভরবৃদ্ধি ও ভর শক্তি সম্পর্ক : E = mc2

আজকে আমরা ভরের আপেক্ষিকতা : ভরবৃদ্ধি ও ভর শক্তি সম্পর্ক : E = mc2 সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৮ এর  আধুনিক পদার্থবিজ্ঞান এর অন্তর্ভুক্ত।

ভরের আপেক্ষিকতা : ভরবৃদ্ধি ও ভর শক্তি সম্পর্ক : E = mc2

ভরের আপেক্ষিকতা (The Relativity of Mass):

ভরের পরিমাপ সকল কাঠামোতে সমান নয় অর্থাৎ ভর পরম নয়। দুটি জড় প্রসঙ্গ কাঠামোর মধ্যে যদি আপেক্ষিক গতি থাকে তবে একই ভরের কোনো বস্তু দুই কাঠামোতে অবস্থিত দুইজন পর্যবেক্ষকের নিকট বস্তুটির পরিমাপকৃত বস্তুর ভর সমান হবে না। স্থির জড় প্রসঙ্গ কাঠামোর পর্যবেক্ষকের নিকট বস্তুর ভর গতিশীল জড় প্রসঙ্গ কাঠামোর পর্যবেক্ষকের পরিমাপকৃত বস্তুর ভর অপেক্ষা বেশী হয়। বস্তুর বেগের কারণে ভরের এই পরিবর্তনকে ভরের আপেক্ষিকতা বলে।

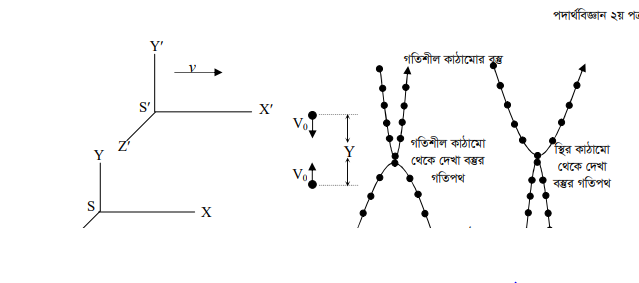
মনে করি, একই ভরের দুটি বস্তুর একটি স্থির জড় প্রসঙ্গ কাঠামো এবং অপরটি গতিশীল জড় প্রসঙ্গ কাঠামোতে আছে। কাঠামো দুটি উলম্বীয় ভাবে পরস্পর হতে Y দূর দিয়ে অতিক্রম করছে এবং গতিশীল জড় প্রসঙ্গ কাঠামোর X-অক্ষ বরাবর বেগ ।। মনে করি কাঠামো দুটি অভিকর্ষ ও অন্য সকল বল থেকে মুক্ত। স্থির কাঠামো S থেকে m ভরের বস্তুকে Y -অক্ষ বরাবর উপর দিকে % বেগে এবং গতিশীল কাঠামো S’ থেকে m ভরের একটি বস্তুকে Y’ অক্ষ বরাবর নীচের দিকে একই সময় একই বেগে নিক্ষেপ করা হলো।

যখন কাঠামো দুটি একই অবস্থানে (যে মুহূর্তে গতিশীল S’ জড় প্রসঙ্গ কাঠামোটি ১ স্থির জড় প্রসঙ্গ কাঠামোটিকে অতিক্রম করছে ঠিক তখনি) তখন বস্তু দুটি পরস্পরের দিকে Y / 2 দূরত্ব অতিক্রম করে পরস্পরে সাথে স্থিতিস্থাপক সংঘর্ষ ঘটিয়ে বিপরীত দিকে পূর্বের অবস্থায় ফিরে গেল। বিশেষ আপেক্ষিক তত্ত্বের প্রথম স্বীকার্য অনুসারে নিজ নিজ কাঠামোতে পর্যবেক্ষক বস্তুর বেগ, ভর ও সময় একই পরিমাপ করবে। যদি পূর্বের Y অবস্থায় ফিরে আসতে সময় লাগে তবে, Voto = 2 x Y/ 2

বা, to = Y/Vo ………………(1)

কিন্তু স্থির কাঠামো S থেকে পর্যবেক্ষক যদি গতিশীল কাঠামো S’ এ অবস্থিত বস্তুর গতি পথ পর্যবেক্ষণ করলে তিনি ভিন্ন চিত্র দেখবেন। কারণ ইতোমধ্যে গতিশীল S’ কাঠামো । বেগে কিছু দূরত্ব অতিক্রম করেছে। সুতরাং S’ কাঠামোর পর্যবেক্ষক বস্তুর ভর ও গতিবেগের মান যা পরিমাপ করেছেন S কাঠামোর পর্যবেক্ষক S’ কাঠামোর বস্তুর ভর ও গতিবেগ তার থেকে ভিন্ন পাবেন। ধরি S কাঠামোর পর্যবেক্ষক কর্তৃক S’ কাঠামোর পরিমাপকৃত বস্তুর ভর, গতিবেগ ও সময় যথাক্রমে m, V 3 t

অতএব, যদি পূর্বের অবস্থায় ফিরে আসতে t সময় লাগে তবে, Vt = 2 x Y/ 2

বা, V = Y/ t ……………..(2)

বিশেষ আপেক্ষিক তত্ত্বের প্রথম স্বীকার্য অনুসারে একই কাঠামোতে নিউটনের সূত্রগুলো সমভাবে প্রযোজ্য। সুতরাং ভরবেগের নিত্যতার সূত্রানুসারে,

moVo+(-mV) = – m0V0 + mV (যেহেতু কাঠামো দুটিতে আদিবেগদ্বয় এবং শেষবেগদ্বয় পরস্পর বিপরীতমুখী)

বা, 2m0V = 2mVo

বা, moV =mVo ……………..(3)

(1) ও (2) নং সমীকরণের মান (3) নং সমীকরণে বসালে, mY/ t=moY/ to

বা, mto = mot ……………..(4)

(1) নং সমীকরণের মান (4) নং সমীকরণে বসালে,

বা, mto = mo .to√(1 – v2/c2)

যেহেতু বস্তুর বেগ কখনই আলোর বেগ অপেক্ষা বেশী বা সমান হতে পারেনা সেহেতু v2/c2<1

অতএব, √(1 – v2/c2) তাই m>mo । অর্থাৎ স্থির জড় প্রসঙ্গ কাঠামো থেকে পরিমাপকৃত গতিশীল জড় প্রসঙ্গ কাঠামোর কোনো বস্তুর ভর স্থির জড় প্রসঙ্গ কাঠামোতে অবস্থিত বস্তুর ভর অপেক্ষা বেশী হয়। যদি v << c হয় তবে v2/c2 ≈0, সেক্ষেত্রে_m = mo হবে। অর্থাৎ সাধারণ বেগে গতিশীল বস্তুর ভরের কোনো পরিবর্তন পরিলক্ষিত হয় না। বস্তুর বেগ যতই আলোর বেগের নিকটবর্তী হবে ভর তত বেশী হবে। এখানে আরো লক্ষণীয় যে, যদি v = c হয় তবে (2) নং সমীকরণে v = c শর্তটি বসালে, m= mo/ 0  = ∞ অর্থাৎ বস্তুর ভর অসীম হয়ে যাবে। সুতরাং, বাড়বে কোনো বস্তুকণা বেগ কখনোই আলোর বেগের সমান বা তারচেয়ে বেশী হতে পারে না ।

ভর শক্তি সম্পর্ক (Mass – Energy Relation)

আইনস্টাইনের বিশেষ আপেক্ষিক তত্ত্বের সবচেয়ে গুর“ত্বপূর্ণ অবদান হলো ভর শক্তি সম্পর্ক। চিরায়ত বলবিদ্যায় কোনো বস্তুর ভর ধ্র“ব রাশি এবং শক্তি সর্বদাই নিত্য। চিরায়ত বলবিদ্যায় আরো ধরা হয় যে, ভর এবং শক্তি দুটি ভিন্ন সত্তা । আইনস্টাইনের বিশেষ আপেক্ষিক তত্ত্বে চিরায়ত বলবিদ্যায় পুরাতন ধারণার আমূল পরিবর্তন ঘটে। এই তত্ত্বানুসারে ভর এবং শক্তি দুটি অভিন্ন সত্তা। ভরকে সম্পূর্ণরূপে ধ্বংস করা যায় এবং তা থেকে শক্তির উৎপন্ন হয়। অর্থাৎ ভর সম্পূর্ণরূপে শক্তিতে রূপান্ডুর হয় এবং একই ভাবে শক্তিও উপযুক্ত পরিবেশ পেলে ভরে রূপান্ডুর হয়।

নিউটনের দ্বিতীয় সূত্রানুসারে ভরবেগের পরিবর্তনের হার প্রযুক্ত বলের সমান, অর্থাৎ F = d/dt(mv)

একটি গতিশীল বস্তুকে স্থির অবস্থায় আনতে যে পরিমান কাজ করতে হয় তাকে গতিশক্তি বলে ।

অতএব, K = ∫Fds = ∫d/dt(mv)ds = ∫(mdv/dt + vdm/dt)ds

বা, K = ∫(mds/dt.dv + vds/dt.dm)

K =∫(mvdv+v²dm) ……………..(5)

আমরা ভরের আপেক্ষিকতা থেকে পাই, m= mo √(1-v2/c²)

বা, m2 = mo2 /(1-v2/c²)

বা, m²(1-v2/c²) = mo2

বা, m² -1/c².v2m² = mo2

ব্যবকলন করে পাই, 2mdm -1/c2 (2vm²dv + 2mv2dm) = 0

বা, (2mc2-2mv2)dm=2vm² dv

বা, (c²-v²)dm =

বা, c²dm = mvdv + v²dm ……………..(6)

(6) নং সমীকরণের মান (5) নং সমীকরণে বসালে,

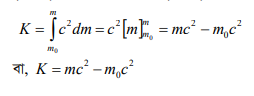
বা, mc² = K+mc²

moc2 হলো স্থির ভরের শক্তি সুতরাং এটি স্থিতি শক্তি। একে V দিয়ে প্রকাশ করলে,  mc² = K +V

সুতরাং, E = mc2 ……………..(7)

এটিই আইনস্টইনের বিখ্যাত ভর-শক্তি সমীকরণ। এই সমীকরণ প্রমাণ করে, ভর ও শক্তি ভিন্ন সত্তার নয়, বরং একই সত্তার দুটি ভিন্নরূপ মাত্র। নিউক্লিয় ফিশান ও ফিউশনের ফলে আমরা যে শক্তি পাই তা এই সমীকরণ দিয়ে সঠিক ভাবে পরিমাপ করা যায়। সূর্য ও অন্যান্য নক্ষত্র থেকে আমরা যে শক্তি পেয়ে থাকি তাও এই সমীকরণ দিয়ে ব্যাখ্যা করা যায়। অর্থাৎ এই সমীকরণ মহাজগতিক সকল শক্তির ব্যাখ্যা দিতে সক্ষম।

শূন্য নিশ্চল ভরবিশিষ্ট কণার ভরবেগ (Momemtum of Particle with Zero Restmass):

আমরা আইনস্টাইনের থেকে পাই, মোট শক্তি E = mc2 = moc2/√(1-v2/c²)

বা, E2 = mo2c4/(1-v2/c²) ……………..(8)

এবং ভরবেগ P = mv= mov/√(1-v2/c²)

বা, p2 = mo2v2/(1-v2/c²)

বা, p2c2 =  mo2v2c2 /(1-v2/c²) ……………..(9)

(8) নং সমীকরণের সাথে (9) নং সমীকরণ বিয়োগ করে পাই,

E2 – p2c2 = mo2c4/(1-v2/c²) = mo2v2c²/(1-v2/c²)

বা, E2 – p2c2 =  mo2c²/(1-v2/c²).(c² -v2)

বা, E2 – p2c2 = mo2c2/(1/c2)(c² -v2) =  Fe 2 – v2 ) = mo2c4

বা, E2 = p2c2 + mo2c4

বা, E = √(p2c2 + mo2c4) …………….(10)

যদি, নিশ্চল ভর mo = 0 হয় তবে, E = √p²c² = = pc

বা, P = E/c …………….(11)

একটি শূন্য নিশ্চল ভরবিশিষ্ট কণার ভরবেগ।

উদাহরণ ১:

একটি বস্তুকণা – বেগে গতিশীল আছে। বস্তুটির স্থির অবস্থায় ভর এবং গতিশীল অবস্থায় ভরের অনুপাত বের করন।

সমাধান :

দেয়া আছে, v = c/4

ভরের আপেক্ষিকতা থেকে আমরা পাই, m= mo/√(1-v2/c²)

বা, mo /m  = √(1-v2/c²)

মান বসালে, mo/ m = √{1-(c/4)2/c2} = √ (1 – 1/16 ) =√0.9375 = 0.968

সুতরাং, mo : m= 0.968:1

উ: mo:m=0.968:1

উদাহরণ ২:

একটি ইলেকট্রনকে ভর-শক্তি রূপার প্রক্রিয়ায় সম্পূর্ণরূপে শক্তিতে রূপাশ্চ্ররিত করলে কি পরিমাণ শক্তি পাওয়া যায় MeV এককে বের কর ন ।

সমাধান :

দেয়া আছে,

me = 9.1×10 kg এবং E = ?

ভর-শক্তির সমীকরণ থেকে আমরা জানি, E = mc2

মান বসালে, E = 9.1×10-31 × (3×108 )2 = 8.19×10-4 J

বা, E = 8.19×10-14/ 1.6×10-19 eV

=5.11875×10 eV≈ 0.5MeV

উ: 0.5MeV

উদাহরণ ৩:

কোনো একটি বস্তুর মোট শক্তি এর স্থিতাবস্থার শক্তির দ্বিগুণ। বস্তুটির বেগ নির্ণয় করন।

সমাধান :

দেয়া আছে,

E = 2Ep

বা, mc² = 2moc², v=?

আমরা ভর-শক্তির সমীকরণ থেকে পাই, E = mc2 = moc²/√(1-v2/c²)

মান বসালে, 2moc2 =  moc²/√(1-v2/c²)

বা, √(1-v2/c²) = 1/2

বা, (1-v2/c²) = 1/4

বা, v2/c² = 1 – 1/4 =0.75

বা, v=√0.75 xc =0.866×3×108

বা, v=2.589×108 ms¹

উ: 2.589×10 ms-1

সার-সংক্ষেপ :

ভরের আপেক্ষিকতাঃ

ভরের পরিমাপ সকল কাঠামোতে সমান নয় অর্থাৎ ভর পরম নয়। দুটি জড় প্রসঙ্গ কাঠামোর মধ্যে যদি আপেক্ষিক গতি থাকে তবে একই ভরের কোনো বস্তু দুই কাঠামোতে অবস্থিত দুইজন পর্যবেক্ষকের নিকট বস্তুটির পরিমাপকৃত বস্তুর ভর সমান হবে না। স্থির জড় প্রসঙ্গ কাঠামোর পর্যবেক্ষকের নিকট বস্তুর ভর গতিশীল জড় প্রসঙ্গ কাঠামোর পর্যবেক্ষকের পরিমাপকৃত বস্তুর ভর অপেক্ষা বেশী হয়।

বস্তুর বেগের কারণে ভরের এই পরিবর্তনকে ভরের আপেক্ষিকতা বলে। m = mo/√(1-v2/c²)

ভর শক্তি সম্পর্ক: E = mc2 , শক্তি ও ভরবেগের সম্পর্ক: E = √(p2c2 + mo2c4)

স্থির ভরহীন কণার ভরবেগ P = E/c

বহুনির্বাচনী প্রশ্নঃ

১। নীচের কোনটি ভর শক্তির সমীকরণ?

ক. E = pc

E=1/2mv2

গ. E = √(p2c2 + mo2c4)

ঘ. E = mc2

২। একটি m ভরের কণার বেগ আলোর বেগের সমান হলে তার ভর কত হবে?

ক. 0

খ. m

গ. mc

ঘ. ∝