আজকে আমরা লরেন্টজ রূপান্তর সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৮ এর আধুনিক পদার্থবিজ্ঞান এর অন্তর্ভুক্ত।
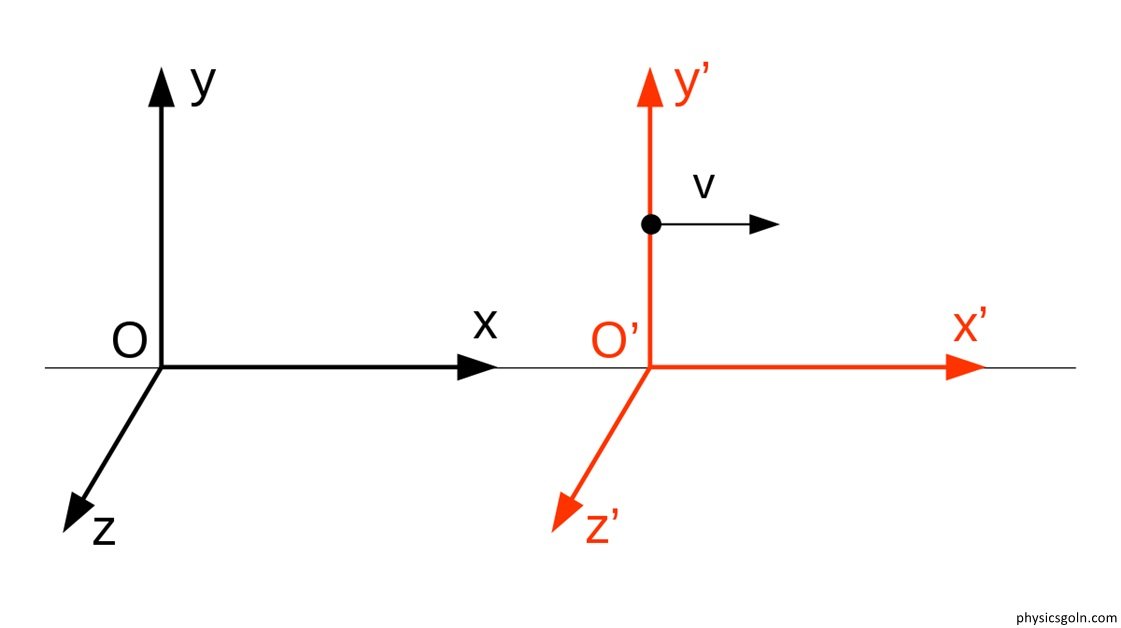
লরেন্টজ রূপান্তর
যেহেতু গ্যালিলিও রূপা বিধি আইনস্টাইনের বিশেষ আপেক্ষিক তত্ত্বের দ্বিতীয় স্বীকার্যের পরিপন্থী। তাই আপেক্ষিকতার বিশেষ তত্ত্বের দ্বিতীয় স্বীকার্য মেনে নেয়া হয় তাহলে ভিন্ন ধরনের রূপান্ডু বিধির অবতারণা করা প্রয়োজন ।
লরেঞ্জ আলোর বেগকে পরমবেগ বিবেচনা করে তার রূপার বিধি উপস্থাপন করেন। তিনি আরো ধরে নেন যে, গতিশীল
কাঠামোর ঘড়ির সময় এবং স্থির কাঠামোর ঘড়ির সময় এক হতে পারেনা। কারণ উভয় কাঠামোতেই আলোর বেগ সমান।
আবার যেহেতু জড় কাঠামোতে পদার্থবিজ্ঞানের সকল সূত্র সমভাবে প্রযোজ্য সেহেতু গতিশীল কাঠামোর পর্যবেক্ষকের পক্ষে
তার ঘড়ির সময়ের ভিন্নতা অনুধাবন করা সম্ভব নয়। সুতরাং লরেঞ্জ ধারণা করেন যে গতিশীল কাঠামোর ঘড়ির প্রতি
সেকেন্ডের মান স্থির কাঠামোর ঘড়ির প্রতি সেকেন্ডের মানের চেয়ে ভিন্ন হবে। সুতরাং t [ যা গ্যলিলিও রূপার বিধি
মানা হয়নি। তাছাড়া লরেঞ্জ আইনস্টেইনের দ্বিতীয় স্বীকার্য সমর্থন করেন।
লরেঞ্জ গ্যলিলিওর একমাত্রিক ও রৈখিক রূপার বিধিগুলো একটি ধ্রুবকের মাধ্যমে প্রকাশ করেন। এই ধ্রুবকটি অবস্থান ও সময়ের উপর নির্ভরশীল এবং গতিশীল কাঠামোর বেগের উপর নির্ভরশীল হতে পারে। যেহেতু গতিশীল কাঠামোর বেগ অপরিবর্তিত থাকে সেহেতু উভয় ক্ষেত্রেই এই ধ্রুবক একই। যদি ধ্রুবকের মান একক হয় তবে লরেঞ্জ রূপান্তর বিধি এবং গ্যালিলিও রূপা বিধি অভিন্ন হবে। লরেঞ্জ রূপান্তর বিধিগুলো লেখা যায়,
x’ = k(x-vt) …………………….(1)
x=k(x’ + vt’) …………………….(2)
y’ = y …………………….(3)
এবং z’ = z …………………….(4)
এবং আইনস্টেইনের দ্বিতীয় স্বীকার্য অনুসারে,
x = ct …………………….(5)
x’ = ct’ …………………….(6)
(1), (2), (3) এবং (4) নং সমীকরণের মাধ্যমে k এর মান নির্ণয় করা যায়। (1) নং সমীকরণে (5) ও (6 ) সমীকরণের মান বসিয়ে পাই,
ct’ = k(ct-vt) = kt(c – v ) …………………….(7)
(2) নং সমীকরণে (5) ও (6) সমীকরণের মান বসিয়ে পাই,
ct = k(ct’ +vt’) = kt’ (c +v) …………………….(8)
(7) ও (8) নং সমীকরণ গুণ করে পাই,
c2tt’ = k²tt'(c²-v²)
বা, k2 = c²/ (c² −v²) = c²/ {c²(1−v²/c²)} = 1/( 1−v²/c²)
বা, k = 1 /√(1-v2/c²) …………………….(9)
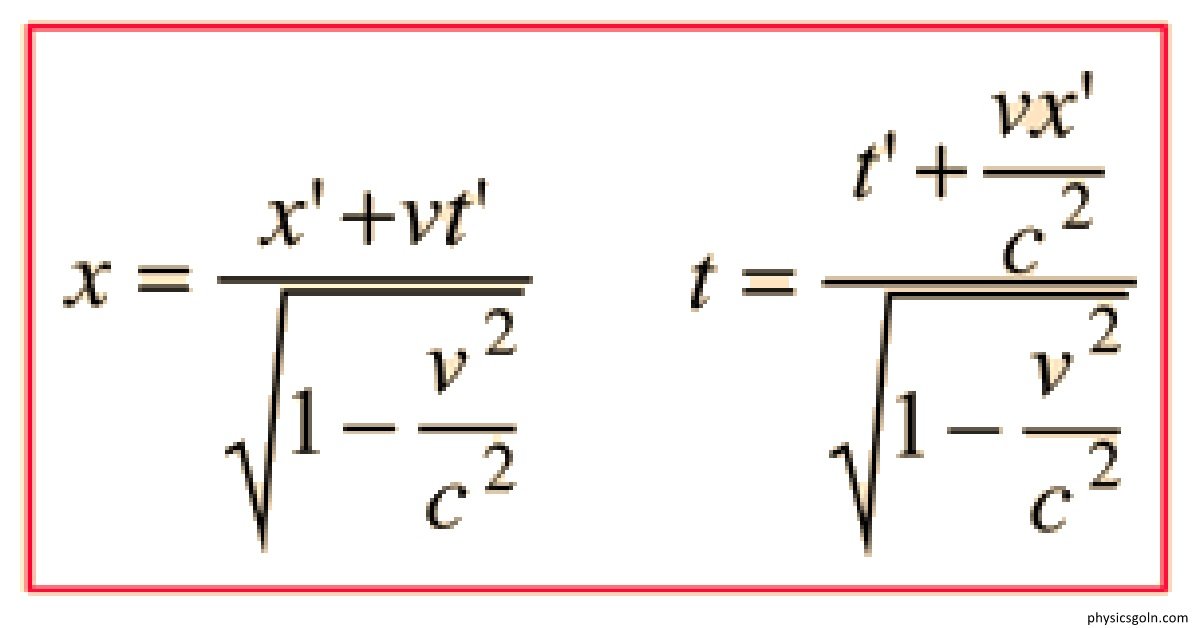
যদি বস্তুর বেগ আলোর বেগের তুলনায় নগন্য হয় অর্থাৎ v<< c হয় তবে (৮.২৩) নং সমীকরণে v2/c2 এর মানকে উপেক্ষা করা যায়, সেক্ষেত্রে লরেঞ্জ রূপান্তর বিধি এবং গ্যালিলিও রূপান্ত্র বিধি অভিন্ন। কিন্তু যদি বস্তুর বেগ আলোর বেগের তুলনায় উপেক্ষণীয় না হয় অর্থাৎ বস্তুর বেগ আলোর বেগের কাছাকাছি হয় তবে v/c2 এর মানকে উপেক্ষা করা যায় না, সেক্ষেত্রে লরেঞ্জ রূপান্তর বিধি এবং গালিলিও রূপা বিধি অভিন্ন নয় ।
(1) ও (2) নং সমীকরণে (9) নং সমীকরণের মান বসালে অর্থাৎ k এর মান বসালে,
x’ = (x-vt)/√(1-v²/c²) …………………….(10)
এবং x = (x’ + vt’)/√(1-v²/c²) …………………….(11)
(10) নং সমীকরণে (5)ও (6) নং সমীকরণের মান বসালে,
ct’ = (ct – v.x/c)/√(1-v²/c²) [যেহেতু _x=ct বা, t=x/c] …………………….(12)
(10) নং সমীকরণে (5) ও (6) নং এর মান বসালে, ct = (ct’ + v.v’/c)/√(1-v²/c² ) [যেহেতু x’=ct’ বা, t’=x/c]
বা, t = (t’- v.x’/c²)/√(1-v²/c²) …………………….(13)
অতএব,
x’ = (x-vt)/√(1-v²/c²)
y’ =y
z’ = z
t’ = (t- v.x’/c²)/√(1-v²/c²) এটাই লরেঞ্জ-এর রূপান্তর বিধি …………………….(14)
এবং
x = (x’ + vt’)/√(1-v²/c²)
y = y’,
z = z’,
t = (t’+ v.x’/c²)/√(1-v²/c²)
একে লরেঞ্জ-এর বিপরীত রূপান্তর বিধি বলে । …………………….(15)
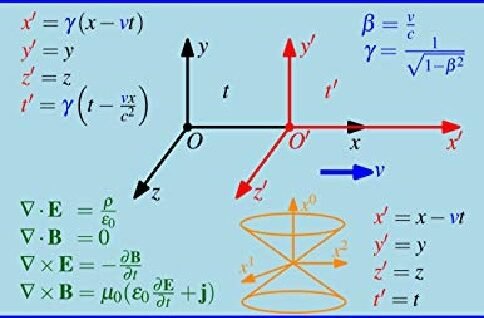
আপেক্ষিক তত্ত্বের প্রমাণ
আপেক্ষিক তত্ত্বের প্রমাণগুলো অনুধাবণ করার জন্য নীচের বিষয়গুলো অত্যন্ড্রু যত্নের সাথে মনে রাখতে হবে।
১। প্রায় সকল ক্ষেত্রেই স্থির কাঠামোর পর্যবেক্ষক গতিশীল কঠামোর বিষয়গুলো পরিমাপ করে।
২। যে পর্যবেক্ষক যে কাঠামোতে থাকে সে তার কাঠামোতে থাকা ঘড়ির সময়কে অনুসরণ করে।
৩। স্থির কাঠামোর পর্যবেক্ষক স্থির কাঠামোতে থাকা বিষয়গুলো পরিমাপের যে মান পাবে, গতিশীল কাঠামোর পর্যবেক্ষক গতিশীল কাঠামোতে থাকা একই বিষয়গুলো পরিমাপের একই মান পাবে।
৪। লরেঞ্জ রূপান্তর বিধিতে কাঠামোর বেগ v এর স্থলে – বসালে লরেঞ্জ-এর বিপরীত রূপান্ডু বিধি পাওয়া যায়।
সার-সংক্ষেপ :
লরেঞ্জ রূপার বিধি :
x’ = (x-vt)/√(1-v²/c²)
y’ = y, z’ = z
t’ = (t’- v.x’/c²)/√(1-v²/c²)
বিপরীত লরেঞ্জ রূপান্তর বিধি:
x = (x’ + vt’)/√(1-v²/c²)
y=y’, z = 2′,
t = (t’+ v.x’/c²)/√(1-v²/c²)
বহুনির্বাচনী প্রশ্ন
১। কি পরিবর্তন করলে লরেঞ্জ রূপান্তর বিধিতে কাঠামো থেকে লরেঞ্জ-এর বিপরীত রূপান্তর বিধি পাওয়া যায়?
ক. x এর স্থলে – x বসালে
খ. c এর স্থলে – C বসালে
গ. t এর স্থলে – বসালে
ঘ. এর স্থলে – বসালে
২। X – অক্ষ বরাবর । বেগে গতিশীল কণার ক্ষেত্রে নীচের কোনটি লরেঞ্জ রূপান্তর বিধি?
ক. x’ = (x-vt)/ √(1-v2/c²)
খ. y’ = (y-vt)/ √(1-v2/c²)
গ. z’ = (z-vt)/ √(1-v2/c²)
ঘ. t’ = (t-vt)/ √(1-v2/c²)
