আজকে আমরা লেন্সের সাধারণ সমীকরণ : বিবর্ধক সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৬ জ্যামিতিক আলোকবিজ্ঞান এর অন্তর্ভুক্ত।
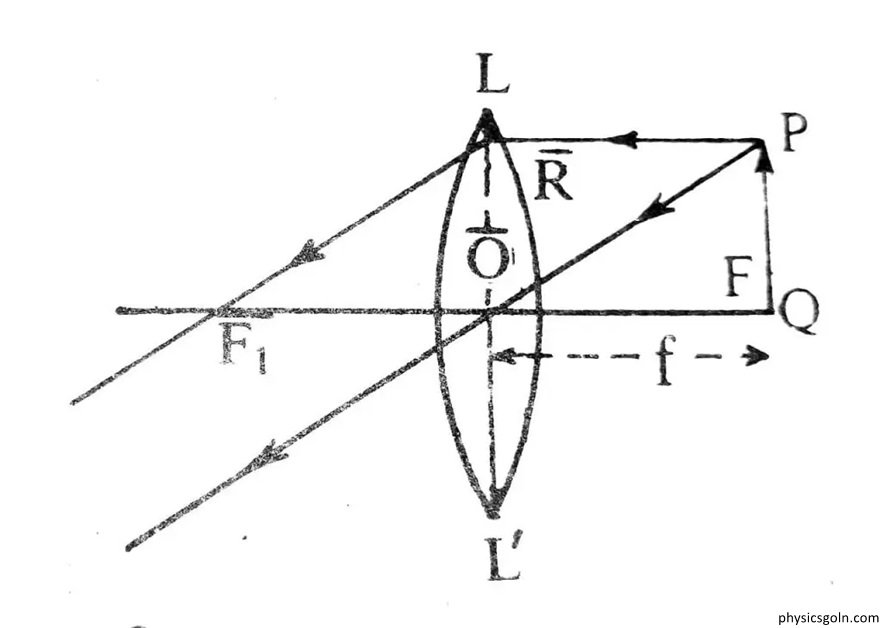
লেন্সের সাধারণ সমীকরণ : বিবর্ধক
সর— উত্তল লেন্সের সাধারণ সমীকরণ (General Lens Equation of Thin Convex Lens):
বস্তু দূরত্ব, প্রতিবিম্ব দূরত্ব এবং ফেকাস দূরত্বের মধ্যে পারস্পরিক সম্পর্ক হলো লেন্সের সাধারণ সূত্র। এবং এদের সমন্বয়ে যে সমীকরণ পাওয়া যায় তাকে লেন্সের সাধারণ সমীকরণ বলে।
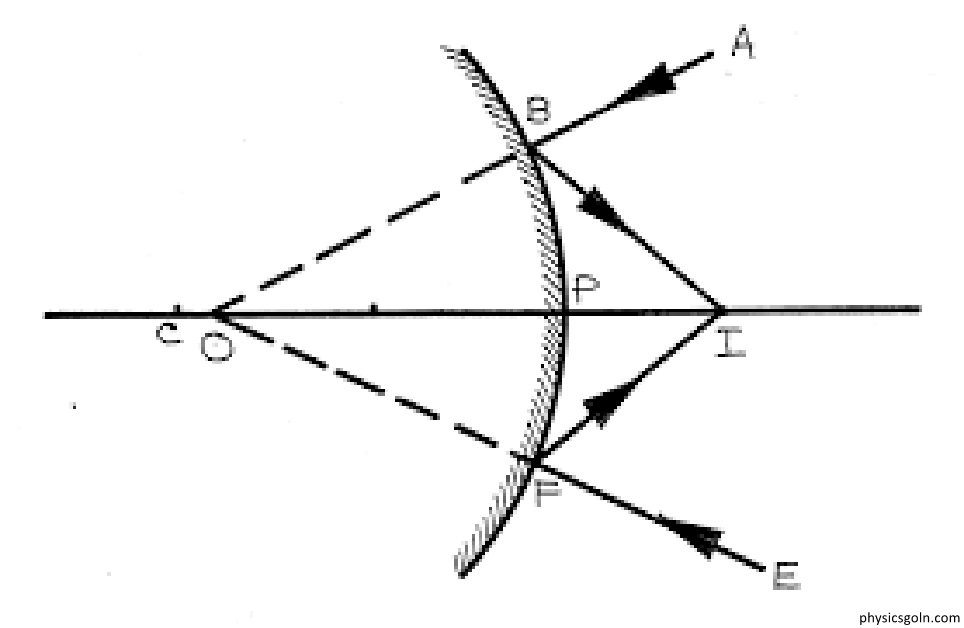
মনে করি, (১ নং চিত্র বাড়ব, ২ নং চিত্র অবাব প্রতিবিম্বের জন্য) OL একটি পাতলা উত্তল লেন্স। PQ একটি বস্তু প্রধান অক্ষের উপর (বাড়ব প্রতিবিম্বের জন্য প্রধান ফোকাসের বাইরে এবং অবাড়ব প্রতিবিম্বের জন্য প্রধান ফোকাসের ভেতরে) Q বিন্দুতে অবস্থিত।
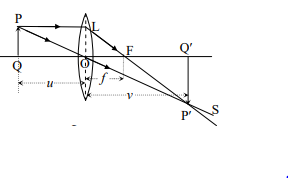
P বিন্দু হতে একটি আলোক রশ্মি প্রধান অক্ষের সমাাল ভাবে লেন্সের L বিন্দুতে আপতিত হবার পর প্রতিসরিত হয়ে প্রধান অক্ষে ফোকাস F বিন্দু দিয়ে LR পথে গমন করে। P বিন্দু থেকে অপর একটি আলোক রশ্মি লেন্সের আলোক কেন্দ্র O তে আপতিত ও প্রতিসরিত হয়ে কোনো বিচ্যুতি bv Nwl‡q OS পথে গমন করে। এই প্রতিসরিত আলোক রশ্মিদ্বয় পরস্পরের (বা প্রতিবিম্বের জন্য সরাসরি এবং অবাড়ব প্রতিবিম্বের জন্য রশ্মিদ্বয়কে পশ্চাৎ দিকে বর্ধিত করলে) সাথে P” বিন্দুতে মিলিত হয়।
সুতরাং P বিন্দুর প্রতিবিম্ব P’ । অতএব P’ বিন্দু থেকে প্রধান অক্ষের উপর অংকিত লম্ব P’Q’ হবে PQ এর প্রতিবিম্ব।

চিত্রানুসারে, ∆POQ এবং ∆P’OQ’ এর মধ্যে ∠POQ = ∠P’OQ’ (বাড়বের জন্য বিপ্রতীপ এবং অবাড়বের জন্য সাধারণ কোণ) এবং PQ ||P Q’ আর ত্রিভুজদ্বয় QOQ’ রেখার উপর অবস্থিত। অতএব ত্রিভুজ দুইটি সদৃশ।
সুতরাং, সদৃশ ত্রিভুজের সূত্রানুসারে, PQ / P’Q’ = OQ/OQ’ ……………………..(1)
আবার, ∆LOF এবং ∆P’Q’F এর মধ্যে ∠LFO = ∠PFQ’ (বাড়বের জন্য বিপ্রতীপ এবং অবাড়বের জন্য সাধারণ কোণ), OL||P’Q’ এবং ত্রিভুজদ্বয় OFQ’ সরল রেখার উপর অবস্থিত। অতএব ত্রিভুজদ্বয় সদৃশ ।
সুতরাং, OL/P’Q’ = OF/Q’F ……………………..(2)
যেহেতু, PL||OQ এবং OL||PQ সেহেতু, OL = PQ |
সুতরাং, (2) নং সমীকরণকে লেখা যায়, PQ/P’Q’ = OF/Q’F ……………………..(3)
(1) ও (3) নং সমীকরণ থেকে লেখা যায় OQ/OQ’ = OF/Q’F ……………………..(4)
বাস্তব প্রতিবিম্বের ক্ষেত্রে :
চিত্রানুসারে, Q’F =OQ’-OF ।
সুতরাং, 4 নং সমীকরণকে লেখা যায়, OQ/OQ’ = OF/(OQ’ – OF)
চিত্রানুসারে, OQ = বস্তুর দূরত্ব = u, OQ’ = প্রতিবিম্ব দূরত্ব = v এবং OF = ফোকাস দূরত্ব = f ।
মান বসালে, u/v = f /(v-f)
বা, uv – uf =vf
De‡ii mgxKiYwU†K uvf w`‡qfvMK‡icvB, uv/uvf – uf/uvf = vf/uvf
বা, ev, 1/f – 1/v = 1/u
বা, 1/v + 1/u = 1/f ……………………..(5)
অবাড়ব প্রতিবিম্বের ক্ষেত্রে ঃ
চিত্রানুসারে, Q’F = OQ’ + OF ।
সুতরাং 4 নং সমীকরণকে লেখা যায়, OQ/OQ’ = OF/(OQ’+OF)
চিত্রানুসারে, OQ = বস্তুর দূরত্ব = u, OQ’ = অবাস্তব প্রতিবিম্ব দূরত = – v এবং OF = ফোকাস দূরত্ব = f
মান বসালে, u/-v= f /-v+f
বা, -uv+uf = -vf
De‡ii mgxKiYwu‡K uvf w`‡qfvM K‡i cvB, -uv/uvf + uf/uvf = -vf/uvf
ev, -1/f + 1/v = -1/u
অতএব, 1/v + 1/u = 1/f ……………………..(6)
সর— অবতল লেন্সের সাধারণ সমীকরণ (General Lens Equation of Thin Concave Lens):
মনে করি, চিত্রে OL একটি পাতলা অবতল লেন্স। PQ একটি বস্তু প্রধান অক্ষের উপর Q বিন্দুতে অবস্থিত। P বিন্দু হতে একটি আলোক রশ্মি প্রধান অক্ষের সমাাল ভাবে লেন্সের L বিন্দুতে আপতিত হবার পর প্রতিসরিত হয়ে LR পথে গমন করে। এই রশ্মিকে পশ্চাৎ দিতে বর্ধিত করলে প্রধান অক্ষের ফোকাস F বিন্দু দিয়ে অতিক্রম করবে। P বিন্দু থেকে অপর একটি আলোক রশ্মি লেন্সের আলোক কেন্দ্র O তে আপতিত ও প্রতিসরিত হয়ে OS পথে গমন করে। এই প্রতিসরিত আলোক রশ্মিদ্বয়কে পশ্চাৎ ভাগে বর্ষিত করলে পরস্পরের সাথে P বিন্দুতে মিলিত হয়। সুতরাং P বিন্দুর প্রতিবিম্ব P’। অতএব P’ বিন্দু থেকে প্রধান অক্ষের উপর অংকিত লম্ব P’Q’ হবে PQ এর প্রতিবিম্ব।
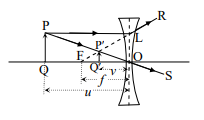
চিত্রনুসারে, ∆POQ এবং ∆P’OQ’ এর মধ্যে ∠POQ = ∠P’OQ’ ( সাধারণ কোণ) এবং PQ || P’Q’ আর ত্রিভুজদ্বয় POQ এবং PO’Q’, QQ’O রেখাদ্বয়ের মধ্যে অবস্থিত। অতএব ত্রিভুজ দুইটি সদৃশ।
সদৃশ ত্রিভুজের সূত্রানুসারে, সুতরাং, PQ/OQ’=OQ/OQ’ ……………………..(7)
আবার, ∆LOF এবং ∆P’Q’F এর মধ্যে ∠LFO = ∠P’FQ’ (সাধারণ কোণ), OL||P’Q’ এবং ত্রিভুজদ্বয় OQ’F এবং LP’F রেখাদ্বয়ের মধ্যে অবস্থিত। অতএব ত্রিভুজদ্বয় সদৃশ।
সুতরাং, OL/P’Q’ = OF/Q’F ……………………..(8)
যেহেতু, PL||OQ এবং OL||PQ সেহেতু, OL = PQ |
সুতরাং (8) নং সমীকরণকে লেখা যায়,
PQ/P’Q’ = OF/Q’F ……………………..(9)
(6) ও (8) নং সমীকরণ থেকে লেখা যায় PQ/OQ’ = OF/Q’F …………………….(10)
চিত্রানুসারে, Q’F = OF – OQ’
সুতরাং, (10) নং সমীকরণকে লেখা যায়, OQ/OQ’ = OF/(OF-OQ’)
চিত্রানুসারে, OQ = বস্তুর দূরত্ব = u, OQ’ = প্রতিবিম্ব দূরত = –v Ges OF = ফোকাস দূরত্ব =−f |
মান বসালে, u/-v = -f /-f-(-v)
বা, – uf + uv=vf
De‡ii mgxKiYwU†K uvf w`‡qfvMK‡icvB uf/uvf + uv/uvf = vf /uvf
বা, -1/v + 1/f = 1/u
অতএব, অতএব, 1/f = 1/v + 1/u ……………………..(11)
(5), (6) এবং (11) নং সমীকরণ থেকে এটাই প্রমাণিত হয় যে, প্রতিবিম্ব বাড়ব হোক বা অবাড় হোক লেন্স উত্তল হোক বা অবতল হোক সকল ক্ষেত্রেই লেন্সের জন্য একটাই সাধারণ সমীকরণ।
এখানে আরো উলণ্ঢখ্য যে, উত্তল লেন্সের ফোকাস দূরত্ব সর্বদাই ধনাত্মক এবং অবতল লেন্সের ফোকাস দূরত্ব সর্বদাই ঋণাত্মক। বাড়ব প্রতিবিম্ব ধনাত্মক এবং বাস্তব প্রতিবিম্ব ঋণাত্মক।
সুতরাং, (1) নং চিত্রের ক্ষেত্রে সমীকরণ, 1/f = 1/v + 1/u (GLv‡b, D‡j †jY Ges বাড়ব প্রতিবিম্ব)
(2) নং চিত্রের ক্ষেত্রে সমীকরণ, 1/f = 1/-v + 1/u ev, 1/f = -1/v + 1/u (GLv‡b, D‡j †jY Ges Aবাড়ব প্রতিবিম্ব)
(3) নং চিত্রের ক্ষেত্রে সমীকরণ, 1/-f = 1/-v + 1/u ev, 1/f = 1/v – 1/u(GLv‡b, AeZj tjY Ges Aবাড়ব প্রতিবিম্ব)
লেন্সের ক্ষেত্রে বিবর্ধন (Magnification by Lens):
কোনো লেন্সে দিয়ে সৃষ্টি প্রতিবিম্বের দৈর্ঘ্য বা উচ্চতা এবং বস্তুর দৈঘ্য বা উচ্চতার অনুপাতকে ঐ প্রতিবিম্বের রৈখিক বিবর্ধন বা সংক্ষেপে বিবর্ধন বলে। রৈখিক বিবর্ধনকে m দিয়ে সূচিত করা হয়। 1,2,3 নং চিত্র থেকে পাওয়া যায়,
m = প্রতিবিম্বের দৈর্ঘ্য বা উচ্চতা (I)/ বস্তুর দৈর্ঘ্য বা উচ্চতা (O) = _ P’Q’/PQ = v/u = প্রতিবিম্ব দূরত্ব/ বস্তু দূরত্ব
চিহ্নের নিয়ম অনুসারে, প্রতিবিম্ব উল্টা অর্থাৎ অবশীর্ষ হলে বিবর্ধন ঋণাত্মক হয় এবং সোজা অর্থাৎ সমশীর্ষ হলে বিবর্ধন ধনাত্মক হয়।
সুতরাং, বিবর্ধন, m = – v/u ……………………..(12)
তাই বিবর্ধন ঋণাত্মক হলে প্রতিবিম্ব বাড়ব এবং বিবর্ধন ধনাত্মক হলে প্রতিবিম্ব অবাস্তব হবে।
যদি, বিবর্ধনের শুধু মানের প্রয়োজন হয় তবে বিবর্ধনকে লেখা যায় \m\ = v/u ……………………..(13)
উদাহরণ ১:
15cm ফোকাস দূরত্বের একটি লেন্স থেকে 45 cm দূরে 2cm দৈর্ঘ্যের একটি বস্তু রাখা হলো। প্রতিবিম্বের অবস্থান আকার ও প্রকৃতি নির্ণয় করন।
সমাধানঃ
দেয়া আছে, f = 15cm = 0.15m, u = 45 cm = 0.45m, O = 2cm, v =?, m=?
আমরা জানি,
লেন্সের সাধারণ সূত্র, 1/v +1/u = 1/f
বা, uf/(u-f)
উত্তল লেন্সের জন্য মান বসালে, v = (0.45×0.15)/( 0.45-0.15) = (0.45×0.15)/ 0.3 = 0.45/2 = 0.225 m
সুতরাং উত্তল লেন্সের ক্ষেত্রে প্রতিবিম্ব দূরত্ব 0.225m । প্রতিবিম্ব বাড়ব, উল্টা এবং লেন্সের পিছনে ।
আবার, বিবর্ধন, m =I/O = v/u = 0.225 /0.45 = 0.5
সুতরাং ., উত্তল লেন্সের ক্ষেত্রে প্রতিবিম্ব আকার বস্তু অপেক্ষা ছোট।
m = v/u =3 অতএব, v/u = 3 বা, v=3u
অবতল লেন্সের জন্য মান বসালে, V = 0.45 x (-0.15) / 0.45-(-0.15) = 0.45 x 0.15/0.5 = 0.0675/0.5 = -0.135m
সুতরাং, অবতল লেন্সের ক্ষেত্রে প্রতিবিম্ব দূরত্ব 0.135m । প্রতিবিম্ব অবা, সোজা এবং লেন্সের সামনে ।
আবার, বিবর্ধন, m =I/O = v/u = 0.135/ 0.45 = 0.3
উ: অবতল লেন্সের ক্ষেত্রে প্রতিবিম্ব আকার বস্তু অপেক্ষা ছোট।
উদাহরণ ২:
একটি উত্তল লেন্সের ফোকাস দূরত্ব 15cm । লেন্স থেকে কত দূরে একটি বস্তু রাখলে তিনগুণ বিবর্ধিত (ক) বাড়ব ও (খ) অবাস্তব প্রতিবিম্ব পাওয়া যাবে বের করন।
সমাধানঃ
দেয়া আছে, f = 15cm = 0.15m, m=3
আমরা জানি,
m =v/u = 3 অতএব, v/u = = 3 বা, v = 3u
আমরা লেন্সের সাধারণ সূত্র থেকে পাই,
1/v + 1/u = 1/f
(ক) বাড়ব প্রতিবিম্বের ক্ষেত্রে, 1/3u + 1/u = 1/0.15
ev, 4/3u + = 1/0.15
ev, u = (0.15 x 4)/ 3
= 0.2m
(খ) অবাড়ব প্রতিবিম্বের ক্ষেত্রে, 1/-3u + 1/u = 1/0.15
ev, 2/3u + = 1/0.15
ev, u = (0.15 x 2)/ 3
= 0.1m
D:e*†Ktj†Y††K বাড়ব cÖwZwe‡¤^i +9†i 0.2m এবং অবাস্তব cÖwZwe+n^i +9+ 10.1m দূরে রাখতে হবে ।
সার-সংক্ষেপ :
লেন্সের সাধারণ সমীকরণ, 1/f = 1/v + 1/u
লেন্সের ক্ষেত্রে নিউটনের সমীকরণ: xy = f2
রৈখিক বিবর্ধন:
কোনো লেন্সে দিয়ে সৃষ্টি প্রতিবিম্বর দৈর্ঘ্য বা উচ্চতা এবং বস্তুর দৈঘ্য বা উচ্চতার অনুপাতকে ঐ প্রতিবিম্বের রৈখিক বিবর্ধন বা সংক্ষেপে বিবর্ধন বলে। |m | = -v/ u = (v-f) /f = f /(u-f)
বহুনির্বাচনী প্রশ্ন:
১। একটি উত্তল লেন্সের ফোকাস দূরত্ব f এবং লেন্সে থেকে ॥ দূরে একটি বস্তু অবস্থিত। বস্তুর আকারের সমান এবং উল্টা প্রতিবিম্ব পবার শর্ত হলো
ক. u =2f
খ. u > 2 f
গ . u<2f
ঘ. 0 <u<f
২। একটি সম দ্বি-উত্তল লেন্সের বক্রতার ব্যাসার্ধ R এবং মাধ্যমের প্রতিসরণাঙ্ক 1.5 । লেন্সেটির ফোকাস দূরত্ব-
ক. শূন্য
খ. অসীম
গ. 2R
ঘ. R
