লেন্স তৈরির সমীকরণ

আজকের আলোচনার বিষয়ঃ লেন্স তৈরির সমীকরণ । যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৬ জ্যামিতিক আলোকবিজ্ঞান এর অন্তর্ভুক্ত।

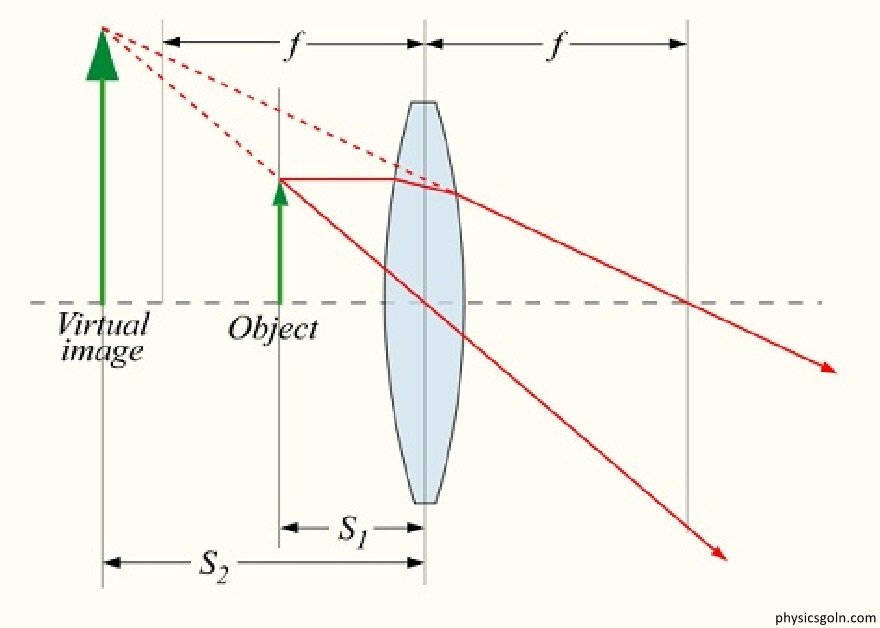
লেন্স তৈরির সমীকরণ

কোনো প্রতিসারক মাধ্যম দুটি গোলীয় পৃষ্ঠ দ্বারা সীমাবদ্ধ হলে লেন্স গঠিত হয়। সুতরাং লেন্সের মধ্য দিয়ে আলোক রশ্মি গমনের সময় দুবার প্রতিসরিত হয়। একবার লেন্সে প্রবেশের সময় ও দ্বিতীয়বার লেন্স থেকে বের হবার সময়।

ধরা যাক, LL’ একটি সর- লেন্স [চিত্র]। লেন্সটি বায়ু মাধ্যমে অবস্থিত। চারপাশ সাপেক্ষে লেন্সের উপাদানের প্রতিসরণাঙ্ক 11 । ধরা যাক, লেন্সের প্রধান অক্ষের উপর P একটি বিন্দু লক্ষ্যবস্তু এবং লেন্সটির আলোক কেন্দ্র O P বস্তু থেকে নিঃসৃত একটি আলোক রশ্মি প্রধান অক্ষ PO বরাবর M বিন্দুতে আপতিত হয়ে সোজাসুজি প্রতিসরিত হয়।

অপর আলোকরশ্মি লেন্সের প্রথম পৃষ্ঠে প্রতিসরিত হয়ে প্রধান অক্ষের উপরস্থ Q’ বিন্দুতে বিশ্ব গঠন করে। সুতরাং Q’ হবে দ্বিতীয় পৃষ্ঠের ক্ষেত্রে অবাড়ব লক্ষ্যবস্তু। লেন্সের দ্বিতীয় পৃষ্ঠের বেলায় আলো Q’ বিন্দু থেকে আসছে বলে মনে হয়। রশ্মি দুটি দ্বিতীয় পৃষ্ঠে প্রতিসরণের পর N বিন্দুতে প্রকৃতপক্ষে মিলিত হয়। সুতরাং Q হচ্ছে P বিন্দুর চূড়াড় বাড়ব বিম্ব [চিত্র]।

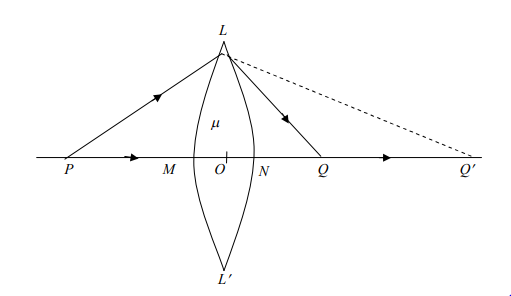
এখন লেন্সের প্রথম পৃষ্ঠে প্রতিসরণ বিবেচনা করলে এবং সর— লেন্স বলে এর পুর“ত্ব উপেক্ষা করলে প্রথম পৃষ্ঠের মের 4, এবং লেন্সের আলোক কেন্দ্র 0 কে একই বিন্দু o বিবেচনা করা যায়। অতএব, লক্ষ্যবস্তুর দূরত্ব OP = u বিম্বের দূরত্ব,
OQ’=v’

আমরা জানি,

μ/v’  + 1/u = (μ – 1)/r1 ……………………..(1)

এখানে r1 লেন্সের প্রথম পৃষ্ঠের বক্রতার ব্যাসার্ধ।

আবার, লেন্সের দ্বিতীয় পৃষ্ঠে প্রতিসরণের সময় আলো লেন্স থেকে বায়ুতে প্রবেশ করেছে। এক্ষেত্রে দ্বিতীয় পৃষ্ঠের মের N এবং লেন্সের আলোক কেন্দ্র O কে একই বিন্দু O বিবেচনা করে

লক্ষ্যবস্তুর দূরত্ব, OQ’ = -v’ [:: অবাব লক্ষ্যবস্তু ]

বিম্বের দূরত্ব, OQ = v

আমরা জানি,

1/v  + μ/-v’ = (1 – μ)/r2 ……………………..(2)

এখানে, r2 লেন্সের দ্বিতীয় পৃষ্ঠের বক্রতার ব্যাসার্ধ।

সমীকরণ (1) ও (2) যোগ করে আমরা পাই,

1/v  + 1/u = (μ – 1)/r1 + (1 – μ)/r2

1/v  + 1/u = (μ – 1)/(1/r1 – 1/r2) ……………………..(3)

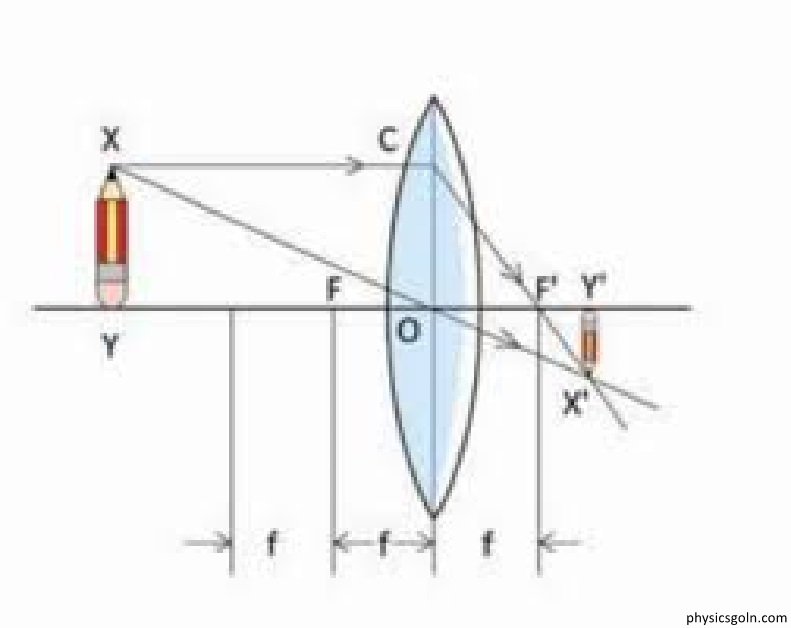
আমরা জানি, বস্তু অসীম দূরত্বে থাকলে প্রতিবিম্ব প্রধান ফোকাসে গঠিত হয়।

অর্থাৎ, u = ∝ হলে, v = f হয়।

সুতরাং (3) সমীকরণ ব্যবহার কর আমরা পাই,

1/f  + 1/∝ = (μ – 1)/(1/r1 – 1/r2)

1/f  = (μ – 1)/(1/r1 – 1/r2) ……………………..(4)

এই সমীকরণকে লেন্সের ফোকাস দূরত্বের সাধারণ সমীকরণ বলে। লেন্স তৈরির কাজে এই সমীকরণ ব্যবহার করা হয় বলে একে লেন্স তৈরির সমীকরণ বা প্রস্তুতকারকের সমীকরণও বলা হয়।

লেন্সের চারপাশের মাধ্যমের প্রতিসরাঙ্ক μm ও লেন্সের উপাদানের প্রতিসরণাক্ত μ1 হলে,

mμ1 = μ1/μm

সুতরাং (4) সমীকরণের রূপ হবে-

1/f  = (μ1/μm – 1)/(1/r1 – 1/r2) ……………………..(5)

এখানে mμ1 = μ1/μm

1/f  = (mμ1 – 1)/(1/r1 – 1/r2) ……………………..(6)

উদাহরণ ১:

একটি দ্বি-উত্তল লেন্সের বক্রতার ব্যাসার্ধ যথাক্রমে 30cm এবং 40cm । যদি মাধ্যমের প্রতিসরণাঙ্ক 1.64 হয় তবে লেন্সটির ফোকাস দূরত্ব নির্ণয় করন।

সমাধানঃ

দেয়া আছে, r1= 30 cm = 0.3m,/2 = 40 cm = 0.4m, μ =1.64 এবং f =?

আমরা জানি, দ্বি-উত্তল লেন্সের ক্ষেত্রে,

লেন্স প্রস্তুতকারকের সূত্র, 1/f = (μ – 1)/(1/r1 + 1/r2)

মান বসালে, 1/f = (0.64 – 1) (1/0.3 + 1/0.4)

বা, 1/f = 0.64 x (0.4+0.3)/( 0.4×0.3) = 0.64 x (0.7/0.12) = 3.73

বা f = 1/3.73 = 0.27m

উ: দ্বি-উত্তল লেন্সটির ফোকাস দূরত্ব 0.27m

উদাহরণ ২:

একটি সম দ্বি-অবতল লেন্সের বক্রতার ব্যাসার্ধ 40cm । মাধ্যমের প্রতিসরণাঙ্ক 3/2। যদি লেন্সটিকে 4/3 প্রতিসরণাঙ্কের মাধ্যমে রাখা হয় তবে লেন্সটির ফোকাস দূরত্ব নির্ণয় করন।

সমাধানঃ

দেয়া আছে, r = 40cm = 0.4m, μb = 3/2 μa = 4/3 এবং f = ?

আমরা জানি, সম দ্বি-অবতল লেন্সের ক্ষেত্রে,

1/f  = -1/r[(μb – μa)/μa]

মান বসালে, 1/f = 1 /0.4[(3/2 – 4/3)/4/3] = 1/0.4 × 1/6 × 3/4 = 0.3125

বা, f = 1/0.3125 = -3.2m

উ: সম দ্বি-অবতল লেন্সটির ফোকাস দূরত্ব 3.2m ।

সার-সংক্ষেপ :

লেন্স প্রস্তুতকারকের গাণিতিক সমীকরণ, 1/f  = (aμb – 1)/(1/r1 – 1/r2)

বা,  1/f  = [(μb – μa)/μa] (1/r1 + 1/r2)

বহুনির্বাচনী প্রশ্নঃ

১। পানির মধ্যে বায়ুর বুদবুদ কী ধরণের লেন্সের কাজ করে?

ক. উভ-উত্তল লেন্স

খ. উভ-অবতল লেন্স

গ. উত্তল-অবতল লেন্স

ঘ. অবতল-উত্তল লেন্স

২। লেন্সের আলো কেন্দ্র একটি নির্দিষ্ট বিন্দু যার অবস্থান

ক. লেন্সের মধ্যে

খ. লেন্সের বাইরে

গ. লেন্সের ফোকাসে

ঘ. লেন্সের প্রধান অক্ষে