আজকের আলোচনার বিষয়ঃ তাড়িতচৌম্বক তরঙ্গ। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৭ ভৌত আলোকবিজ্ঞান এর অন্তর্ভুক্ত।
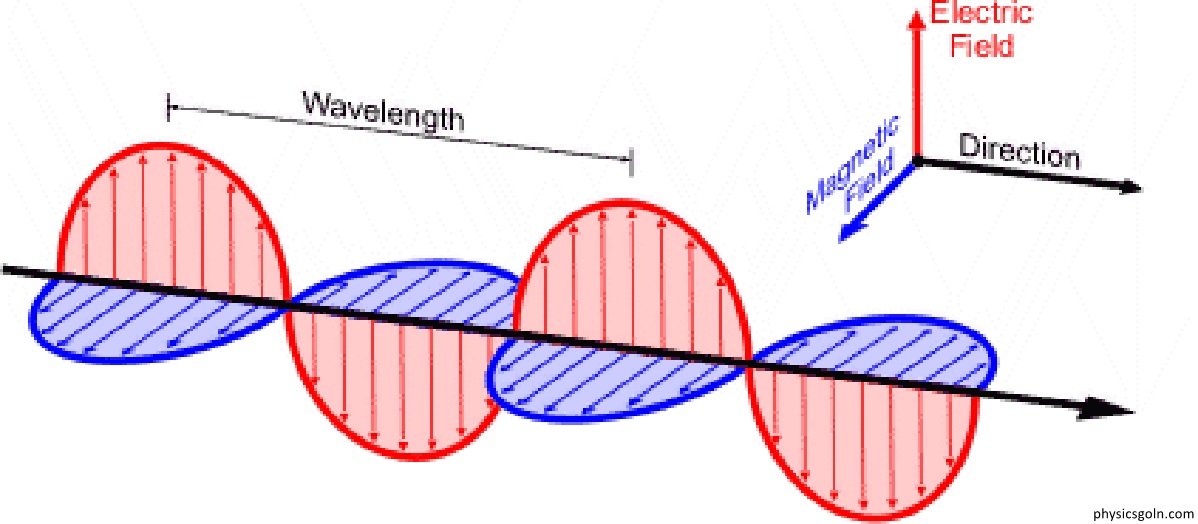
তাড়িতচৌম্বক তরঙ্গ
বিজ্ঞানী জেম্স ক্লার্ক ম্যাক্সওয়েল (James Clerk Maxwell) ১৮৬৫ সালে আলোকে তাড়িত চৌম্বক তরঙ্গরূপে উপস্থাপন করেন। তিনি বলেন আলো তড়িৎক্ষেত্র (Electric field) ও চৌম্বক ক্ষেত্রের (Magnetic field) চলতরঙ্গ অর্থাৎ আলো একটি তড়িৎচুম্বক তরঙ্গ। এই সময় দৃশ্যমান আলো, অবলোহিত ও অতিবেগুনী রশ্মি ছাড়া অন্য কোনো তাড়িত চৌম্বক তরঙ্গের অস্তিত্ব জানা ছিল না।
ম্যাক্সওয়েলের তড়িতচৌম্বক তত্ত্ব অনুসারে, যে কোনো তাড়িত চৌম্বক তরঙ্গের গতি পথের প্রতিটি বিন্দুতে তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্র বিদ্যমান। এই ক্ষেত্র দুটি সরল ছন্দিত স্পন্দনে কম্পিত হতে থাকে এবং এই কম্পন এক বিন্দু থেকে অন্য বিন্দুতে সঞ্চালিত হয়। এই ভাবে তড়িতচৌম্বক তরঙ্গ বিড়ার লাভ করে। তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্র কোনো জড় মাধ্যম ছাড়াই চারিদিকে ছড়িয়ে পরতে পারে। অর্থাৎ তাড়িত চৌম্বক তরঙ্গ সঞ্চালনের জন্য কোনো মাধ্যমের প্রয়োজন হয় না। এই তরঙ্গ শূন্য মাধ্যমেও চলাচল করতে পারে ।
তড়িৎ প্রবাহের চৌম্বক ক্রিয়া অধ্যায়ে আমরা দেখেছি,
অ্যাম্পিয়ারের সূত্র, ∮B.dl = μol ………………….. (1)
এই সূত্রের কিছু সীমাবদ্ধতা আছে। তড়িৎ প্রবাহ পরিবর্তনশীল হলে সমীকরণটি কী রূপ নিবে তা বলা হয় নি। যেমন, কোনো বর্তনীতে ধারক থাকলে ধারকটি যখন চার্জিত হয় বা অচার্জিত হয় তখন বর্তনীতে তড়িৎ প্রবাহের পরিবর্তন ঘটে কিন্তু ধারকের পাতদ্বয়ের মধ্যে কোনো তড়িৎ প্রবাহ হয় না। সুতরাং, এই ক্ষেত্রে উপরের সমীকরণটি প্রযোজ্য হবে না । সমীকরণটির এই ত্র“টি দূর করার জন্য ম্যাক্সওয়েল সমীকরণটির ডানদিকে অতিরিক্ত একটি রাশিমালা যুক্ত করেন।

রাশিটি হলো, μolo = = μoεo.d∅E/dt ………………….. (2)
ম্যাক্সওয়েল Id রাশিটিকে সরণ প্রবাহমাত্রা (displacement current) হিসাবে উলেণ্ঢখ করেন।
এই রাশির εo শূন্য মাধ্যমে তড়িৎ ভেদন যোগ্যতা এবং এবং ∅E = ∫E.ds হলো কোনো গাউসীয় তলের মধ্য দিয়ে অতিক্রাড় তড়িৎ ফ্লাক্স। তাহলে, d∅E/dt হলো তড়িৎ ফ্লাক্সের পরিবর্তনের হার। সুতরাং, Id = εo.d∅E/dt পরিবর্তনশীল তড়িৎক্ষেত্রকে নির্দেশ করে। আর এই পরিবর্তনশীল তড়িৎক্ষেত্রই হলো বর্তনীতে সংযুক্ত ধারকের চার্জিত বা অচার্জিত হবার সময় পাতদ্বয়ের মধ্যবর্তী অঞ্চলে উপস্থিত তড়িৎ প্রবাহের সমতুল্য। সুতরাং এই জাতীয় বর্তনীকে বিছিন্ন বর্তনী হিসাবে ধরা হয় না।
সূতরাং, অ্যাম্পিয়ারের সূত্রের পরিবর্তিত রূপ হলো, ∮B.dl = μoI + μoεo.d∅E/dt ………………….. (3)
যা অ্যাম্পিয়ার-ম্যাক্সওয়েল সূত্র নামে পরিচিত।
তাড়িতচৌম্বক আবেশ অধ্যায়ে আমরা দেখেছি ফ্যারাডের দ্বিতীয় সূত্রানুসারে, E =-nd∅s/dt ………………….. (4)
এই সমীকরণ নির্দেশ করে পরিবর্তিত চৌম্বক ক্ষেত্র তড়িৎ ক্ষেত্রের সৃষ্টি করে।
এই সমীকরণ দুটি সময়ের সঙ্গে পরিবর্তনশীল তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্র সৃষ্টি করে। এই পরিবর্তনশীল তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্র তরঙ্গের মত ছড়িয়ে পড়ে যাকে আমরা তাড়িতচৌম্বক তরঙ্গ বলি ।
অতএব, কোনো স্থানে পরিবর্তনশীল তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্রের অস্তিত্ব থাকলে সেটি যে তরঙ্গ আকারে ছড়িয়ে পড়ে তাকে তাড়িতচৌম্বক তরঙ্গ বলে।
ম্যাক্সওয়েল গাণিতিক ভাবে আরো প্রমাণ করেন যে, শূন্য স্থানে তাড়িতচৌম্বক তরঙ্গের বেগ, v = 1/√μoεo
এখানে, μo = শূন্য স্থানের চৌম্বক প্রবেশ্যতা (permeability) = 1.26 ×10 Hm-1 এবং
εo = শূন্য স্থানের তড়িৎ ভেদনযোগ্যতা (permitivity) = 8.85 x1 02Fm-1
সমীকরণে এই মান বসালে, v = 1 /√(1.26 ×10 x 8.85×10-12 ) = 2.99 ×108 ms-1 ≈ 3×10^ms” = c
শূন্য মাধ্যমে আলোর বেগের সমান হয়। এর থেকে ম্যাক্সওয়েল সিদ্ধার্ল্ড নেন, আলো তাড়িতচৌম্বক তরঙ্গ।
সুতরাং, শূন্য মাধ্যমে আলোর বেগ, c = 1/√μoεo
শুধু আলোই নয়, বেতার তরঙ্গ, মাইক্রো তরঙ্গ, অবলোহিত রশ্মি, অতিবেগুনী রশ্মি, এক্স রশ্মি, গামা রশ্মি ইত্যাদি সবই তাড়িতচৌম্বক তরঙ্গ।
১৮৮৮ সালে জার্মান বিজ্ঞানী হাইনরিচ হার্জ (Heinrich Hertz) সর্বপ্রথম তাড়িতচৌম্বক তরঙ্গ পরীক্ষামূলকভাবে উৎপাদন করেন এবং সনাক্ত করার ব্যবস্থা করেন। তার পরীক্ষার মাধ্যমে ম্যাক্সওয়েলের সমীকরণগুলোর সত্যতা প্রমাণিত হয়।
তাড়িতচৌম্বক তরঙ্গের তরঙ্গ প্রকৃতি ( Wave Nature of Electromagnetic Waves):
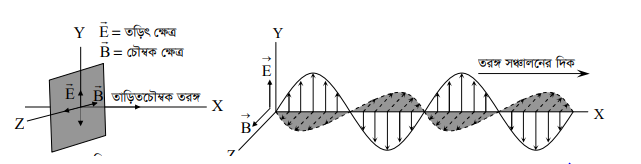
তাড়িতচৌম্বক তরঙ্গের তড়িৎক্ষেত্র É, চৌম্বক ক্ষেত্র B এবং তরঙ্গের গতির অভিমুখ সর্বদাই পরস্পর লম্বভাবে থাকে (চিত্র ৭.১ক)। সুতরাং, তাড়িতচৌম্বক তরঙ্গ এক ধরণের তির্যক তরঙ্গ। (চিত্র ৭.১ক)। ধরা যাক, একটি তাড়িতচৌম্বক তরঙ্গ ধনাত্মক X – অক্ষ বরাবর বিড়ার লাভ করে। সেক্ষেত্রে তড়িৎক্ষেত্র É এবং চৌম্বক ক্ষেত্র B যথাক্রমে Y -অক্ষ এবং Z -অক্ষের সমান্ড্ রালভাবে কম্পনশীল হয়। t সময়ে মূলবিন্দু থেকে x দূরত্বে তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্রকে যে দুটি রাশিমালা দিয়ে প্রকাশ করা হয় তা হলো যথাক্রমে,
E = Eo sin (wt – kx)= Eo sin 2π/λ (ct-x) ………………….. (4)
B = Bo sin (wt-kx) = Bo sin2π/λ (ct – x) ………………….. (5)
এখানে, k হলো তরঙ্গ সংখ্যা। এই দুটি সমীকরণ চলতরঙ্গের সমীকরণ। এই দুটি ক্ষেত্রের কোনোটিই প্রকৃতিতে একক ভাবে থাকতে পারে না। তাড়িতচৌম্বক তরঙ্গ, তড়িৎক্ষেত্র তরঙ্গ ও চৌম্বক ক্ষেত্র তরঙ্গের কম্পাঙ্ক সমান এবং উভয়ের দশা একই। দুটি ক্ষেত্র অনবরত একে অপরকে আবেশের মাধ্যমে সৃষ্টি করে চলে এবং ক্ষেত্র দুটির সাইনধর্মী (Sinusodial) পরিবর্তনই তরঙ্গ হিসাবে এগিয়ে চলে। (৭.১খ) চিত্রে তড়িৎক্ষেত্র তরঙ্গ XY-তলে ও চৌম্বকক্ষেত্র তরঙ্গ XZ-তলে অবস্থান করছে এবং তাড়িতচৌম্বক তরঙ্গ X-অক্ষ বরাবর অগ্রসর হচ্ছে। ম্যাক্সওয়েল আরো দেখান যে, তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্রের বিারের অনুপাত থেকেও তাড়িতচৌম্বক তরঙ্গের বেগের মান পাওয়া যায় ।
অর্থাৎ, Eo/ Bo = c ………………….. (6)
(4) ও (5) নং সমীকরণ থেকে লেখা যায়,
E/B = Eo sin (wt – kx)/Bo sin (wt-kx) = Eo/Bo
E/B = Eo/Bo = c ………………….. (7)
কোনো তাড়িতচৌম্বক তরঙ্গের তরঙ্গদৈর্ঘ্য 2, কোনো মাধ্যমে তরঙ্গের কম্পাঙ্ক । হলে ঐ মাধ্যমে তরঙ্গের বেগ হবে vi । মাধ্যম পরিবর্তন হলে তরঙ্গদৈর্ঘ্যর তথা বেগের মানের পরিবর্তন হয়ে যায় কিন্তু কম্পাঙ্ক অপরবর্তিত থাকে ।
তাড়িতচৌম্বক বর্ণালী (Electromagnetic Spectrum) :
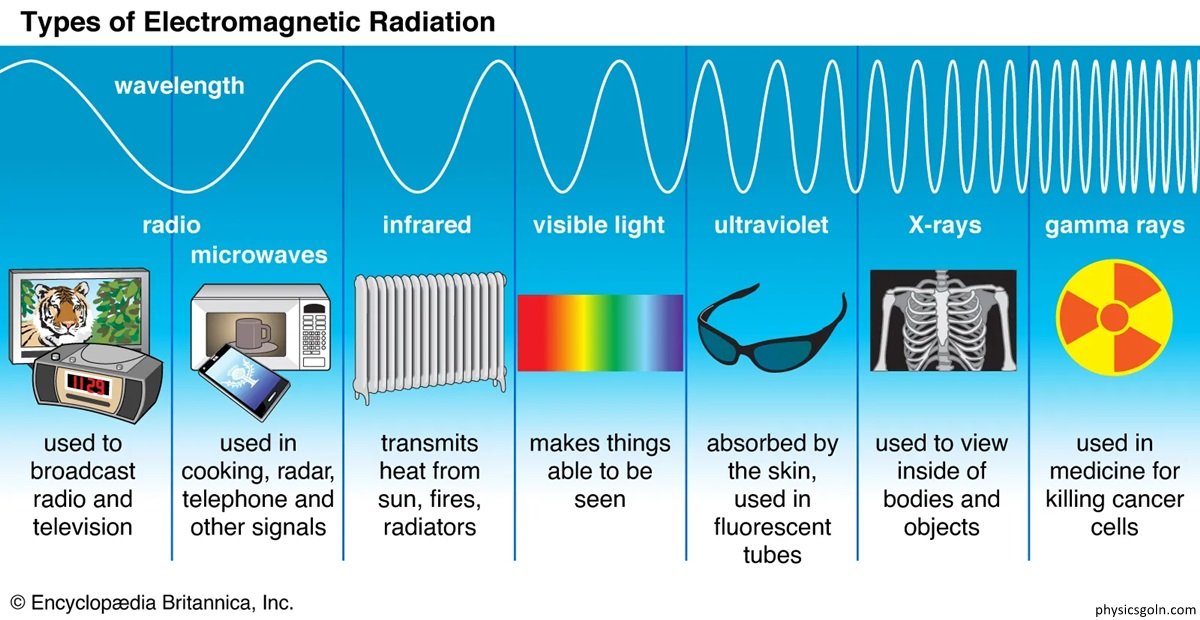
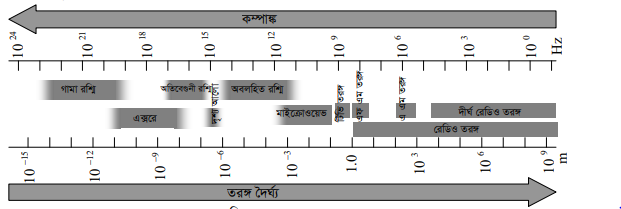
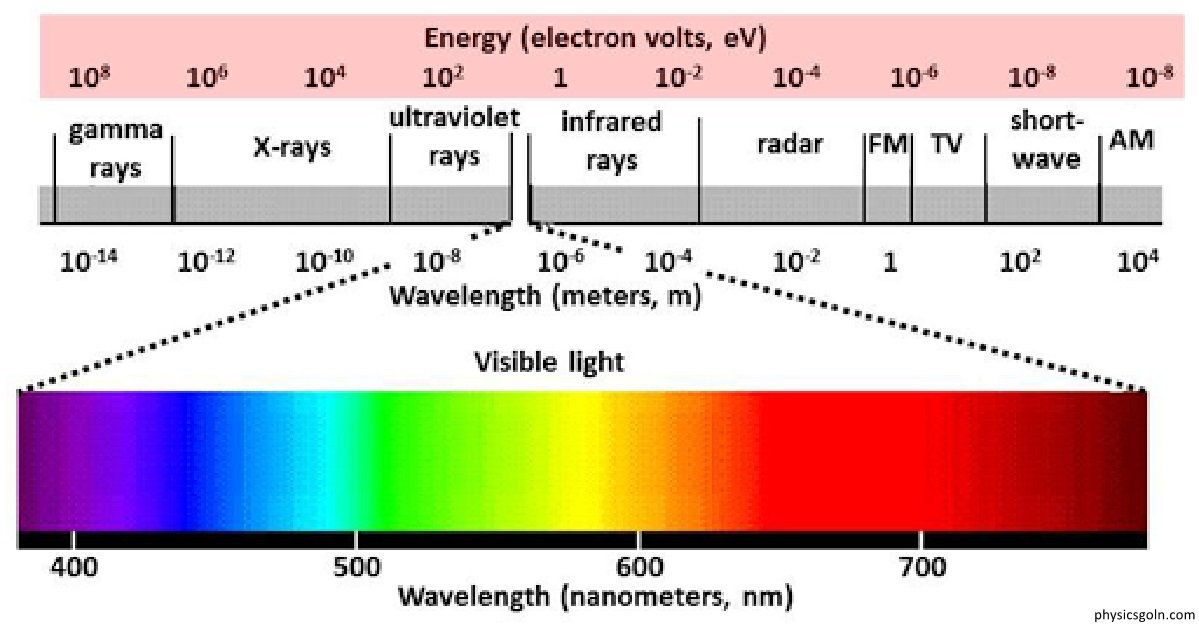
এখন আমরা তাড়িতচৌম্বক বর্ণালী বিষয়ে আলোচনা করবো। তাড়িত চৌম্বক বর্ণালীর বিভিন্ন তরঙ্গদৈর্ঘ্যের তরঙ্গের মাঝে আমরা ডুবে আছি। কিছু বিশেষ বৈশিষ্ট্য ও ব্যবহারের উপর ভিত্তি করে তাড়িতচৌম্বক তরঙ্গের বিভিন্ন তরঙ্গদৈর্ঘ্য পালণ্ঢার কয়েকটি শ্রেণীতে বিভক্ত করা হয়েছে। তরঙ্গদৈর্ঘ্যের ক্রমানুসারে রেডিও তরঙ্গ, মাইক্রোওয়েভ, অবলোহিত রশ্মি, দৃশ্যমান আলো, অতিবেগুণী রশ্মি, এক্সরে, গামা রশ্মি হলো কয়েকটি উলেণ্ঢখযোগ্য তাড়িতচৌম্বক তরঙ্গ। (৭.২ নং) চিত্রে তাড়িত চৌম্বক বর্ণালীর তরঙ্গদৈর্ঘ্য ও কম্পাঙ্কের বিন্যাস দেখানো হয়েছে। বর্ণনার সুবিধার জন্য তাড়িত চৌম্বক বর্ণালীর ভিন্ন ভিন্ন তরঙ্গদৈর্ঘ্যর পালণ্ডায় অবস্থিত তাড়িতচৌম্বক তরঙ্গগুলোকে ভিন্ন ভিন্ন নাম দেয়া হয়েছে। বিভিন্ন তরঙ্গদৈর্ঘ্যের পালণ্ডার একটি তালিকা এবং এর বিভিন্ন অংশের বর্ণনা নিচে দেয়া হলো তবে তরঙ্গদৈর্ঘ্যের এই পালণ্ঢা খুব সুনির্দিষ্ট নয়।
তাড়িতচুম্বক তরঙ্গ | তরঙ্গ দৈর্ঘ্যে পালণ্ঢা | উৎস | ব্যবহার |
| রেডিও তরঙ্গ | 0.1m থেকে 104m | কোনো পরিবাহী তারের মধ্য দিয়ে গতিশীল চার্জ, LC স্পন্দকের মত ইলেকট্রনিক যন্ত্রপাতি ইত্যাদি। | মোবাইল ফোন, বিমান চালনা, রেডিও এবং টিভি ত্বরণসহ | সংক্রাড় যোগাযোগ ব্যবস্থায় এই তরঙ্গ ব্যবহৃত হয়। |
| মাইক্রোওয়েভ | 10-4 m থেকে 0.3m | বিভিন্ন ইলেকট্রনিক যন্ত্রপাতি | মাইক্রোওয়েভ চুলিণ্টতে এই ধরণের বিকিরণ ব্যবহার করে রান্না করা হয়। রাডার ব্যবস্থায় তথ্য সংগ্রহ করা এবং পদার্থের পারমাণুবিক ও আনবিক ধর্ম পরীক্ষা সংক্রাড় কাজে এই তরঙ্গ তরঙ্গ ব্যবহার করা হয়। |
| অবোলহিত রশ্মি | 7×10-7m থেকে 10-3 m | পদার্থের অণু এবং ঘরের তাপমাত্রায় থাকা কোনো বস্তু হলো এর উৎস। | চিকিৎসা ক্ষেত্রে, কম্পন সংক্রান্ত্ বর্ণালী বিদ্যায় এবং | অবলহিত ফটোগ্রাফিতে এই তরঙ্গ ব্যবহৃত হয়। |
| দৃশ্যমান আলো | 7×10-7m থেকে 4×10-3m | অণু ও পরমাণুর মধ্যে ইলেকট্রনের পুনর্বিন্যাসের কারণে দৃশ্যমান আলোর নিঃসরিত হয়। | এই তরঙ্গ আমাদের দেখার অনুভূতি জাগায়। লাল বর্ণ থেকে বেগুনী বর্ণ এই এঈ তরঙ্গের সীমা। |
| অতিবেগুণী রশ্মি | 6×10-8m থেকে 4×10-7m | সূর্য। | সূর্যালোকের অতিবেগুনী রশ্মির উপস্থিতিতে ত্বকে ভিটামিন D সংশেষিত হয়। ত্বকের বিভিন্ন রোগ নিরাময়ে এই রশ্মি ব্যবহার করা হয়। |
| এক্সরে | 10 -11 থেকে 10-8m | উচ্চ গতিশক্তি সম্পন্ন ইলেকট্রন স্রোত দিয়ে আঘাত প্রাপ্ত ধাতব লক্ষ্যবস্তু। | বিভিন্ন প্রকার রোগের কারণ অনুসন্ধানে, ক্যান্সার | কোষ ধ্বংসের জন্য এই রশ্মি ব্যবহার করা হয়। তবে | এই রশ্মি কোনো জীবিত কোষে আপতিত হলে সেই কোষ ধ্বংস করে। কেলাসিত পদার্থের গঠন অনুসন্ধানে এই রশ্মি ব্যবহার করা হয়। |
| গামা রশ্মি | 10-11 m থেকে ছোট তরঙ্গদৈর্ঘ্য | এই রশ্মি বৈজ্ঞানিক পরীক্ষা নিরীক্ষায় বেশী ব্যবহৃত হয়। এই রশ্মি কোনো জীবিত কোষে আপতিত হলে সেই কোষ ধ্বংস করে। এর ভেদন ক্ষমতা অত্যধিক বেশী যে পুর= সিসার তৈরি পর্দা ছাড়া এই রশ্মি শোষিত হয় না। |
উদাহরণ ১:
শূন্য স্থানে একটি তাড়িতচৌম্বক বিকিরণের সর্বোচ্চ তড়িৎক্ষেত্র 9×102 NC । এর সর্বোচ্চ চৌম্বক ক্ষেত্র নির্ণয় করন।
সমাধানঃ
দেয়া আছে, Em =9x102NC-1, c=3x108ms এবং B =?
আমরা জানি,
তাড়িতচৌম্বক তরঙ্গের দ্রুতি, c = Em/B m
বা, Bm = Em/c
মান বসালে Bm = 9×102 /3 x108 = 3×10-6 T
উ: 3×10-6 T
উদাহরণ ২:
কোনো স্থানে তাড়িতচৌম্বক তরঙ্গের তড়িৎক্ষেত্র তরঙ্গের সমীকরণ হল, E = 100sin 22 (ct-1) NC λ এর চৌম্বকক্ষেত্র তরঙ্গের সমীকরণ নির্ণয় কর।
সমাধানঃ
দেয়া আছে, E = sin 2π/λ(ct-r), c = 3x108ms-1 এবং B =?
আমরা জানি,
তাড়িতচৌম্বক তরঙ্গের দ্রুতি, c = E/B
বা B = E/c
মান বসালে, B = 60 sin2π/λ(ct – r )/3×108
= 2×10-7sin2π/λ( ct – r ) T উত্তর।
সার-সংক্ষেপ :
তাড়িতচৌম্বক তরঙ্গ:
কোনো স্থানে পরিবর্তনশীল তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্রের অস্ত্বিত্ব থাকলে সেটি যে তরঙ্গ আকারে ছড়িয়ে পড়ে তাকে তাড়িতচৌম্বক তরঙ্গ বলে। তাড়িতচৌম্বক তরঙ্গের তড়িৎক্ষেত্র É, চৌম্বক ক্ষেত্র B এবং তরঙ্গের গতির অভিমুখ সর্বদাই পরস্পর লম্বভাবে থাকে। তাড়িতচৌম্বক তরঙ্গ এক ধরণের তির্যক তরঙ্গ। শূন্য স্থানে
তাড়িতচৌম্বক তরঙ্গের বেগ,c = 1/√μoεo
তাড়িতচৌম্বক বর্ণালী:
কিছু বিশেষ বৈশিষ্ট্য ও ব্যবহারের উপর ভিত্তি করে তাড়িত চৌম্বক তরঙ্গের বিভিন্ন তরঙ্গদৈর্ঘ্য পালণ্ঢার কয়েকটি শ্রেণীতে বিভক্ত করা হয়েছে। তরঙ্গদৈর্ঘ্যের ক্রমানুসারে রেডিও তরঙ্গ, মাইক্রোওয়েভ, অবলোহিত রশ্মি, দৃশ্যমান আলো, অতিবেগুণী রশ্মি, এক্সরে, গামা রশ্মি হলো কয়েকটি উলেণ্ঢখযোগ্য তাড়িতচৌম্বক তরঙ্গ। তাড়িতচৌম্বক বর্ণালীর বিভিন্ন তরঙ্গদৈর্ঘ্যের তরঙ্গের মাঝে আমরা ডুবে আছি।
বহুনির্বাচনী প্রশ্ন
১. নীচের কোনটি তাড়িতচৌম্বক তরঙ্গ নয়?
ক. অতিবেগুনী রশ্মি
খ. এক্সরে
গ. B -রশ্মি
ঘ. গামা রশ্মি
২. শূন্য স্থানে কোনো তাড়িতচৌম্বক তরঙ্গের কোনো বিন্দুতে তড়িৎক্ষেত্র ও চৌম্বক ক্ষেত্রের বিারের অনুপাত
ক. 1/μoεo
খ. 1/√μoεo
গ. μoεo
ঘ. √μoεo
আরও দেখুনঃ
