আজকের আলোচনার বিষয়ঃ তরঙ্গ : হাইগেনস্ এর নীতি। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৭ ভৌত আলোকবিজ্ঞান এর অন্তর্ভুক্ত।
তরঙ্গ : হাইগেনস্ এর নীতি
তরঙ্গ ও তরঙ্গমুখের ধারণা (Concept of Wavefront):
স্থির পানিতে ঢিল ফেললে তরঙ্গের সৃষ্টি হয়। ঢিলটি যেখানে পড়ে সেই স্থান থেকে নির্দিষ্ট বেগে পানির তলের উপর চারিদিকে এই তরঙ্গ ছড়িয়ে পড়ে। পনির কণা কিন্তু তরঙ্গের সাথে অনুভূমিক ভাবে ছড়ায় না বরং একই স্থানে থেকে উলম্ব বরাবর কম্পিত হতে থাকে। ধরা যাক, আলোড়নের কেন্দ্র থেকে কিছু দূরে অবস্থিত একটি পানির কণার উলম্ব সরণ সর্বাধিক। সে সময় আলোড়ন কেন্দ্র অর্থৎ তরঙ্গ উৎস থেকে ঐ কণার দূরত্বের সমান ব্যাসার্ধ বিশিষ্ট বৃত্তের পরিধি উপর অবস্থিত অন্য সব উলম্ব সরণ সর্বাধিক। সুতরাং তরঙ্গ উৎস থেকে সমদূরত্বে থাকা প্রতিটি কণা যে কোনো মুহূর্তে সম দশা সম্পন্ন।
কোনো উৎস থেকে তরঙ্গ যখন শূন্য বা কোনো মাধ্যমে মধ্য দিয়ে সঞ্চালিত হয় তখন শূন্য বা কোনো মাধ্যমের বিন্দুগুলো কম্পিত হতে থাকে। যেকোনো মুহূর্তে একই দশা সম্পন্ন বিন্দুগুলো যে রেখায় বা তলের উপর অবস্থিত থাকে তাকে তরঙ্গমুখ বলে ।
ত্রিমাত্রিক স্থানে কোনো বিন্দু কম্পিত হলে যে তরঙ্গের সৃষ্টি হয় সেটি ত্রিমাত্রিক তরঙ্গ। এই ক্ষেত্রে সেই বিন্দুকে কেন্দ্র করে একটি গোলক কল্পনা করলে ঐ গোলকের পৃষ্ঠের উপর অবস্থিত বিন্দুগুলি সমদশা সম্পন্ন। সুতরাং এই ক্ষেত্রে গোলকীয় তরঙ্গমুখ পাওয়া যাবে। আর যদি গোলকের ব্যাসার্ধ খুব বড় হয় তবে সেক্ষেত্রে গোলকীয় তরঙ্গমুখের ক্ষুদ্র অংশকে সমতল
তরঙ্গমুখ হিসাবে বিবেচনা করা যাবে।
তরঙ্গমুখ সাধারণত তিন প্রকারের হয়;
(ক) গোলীয় তরঙ্গমুখ:
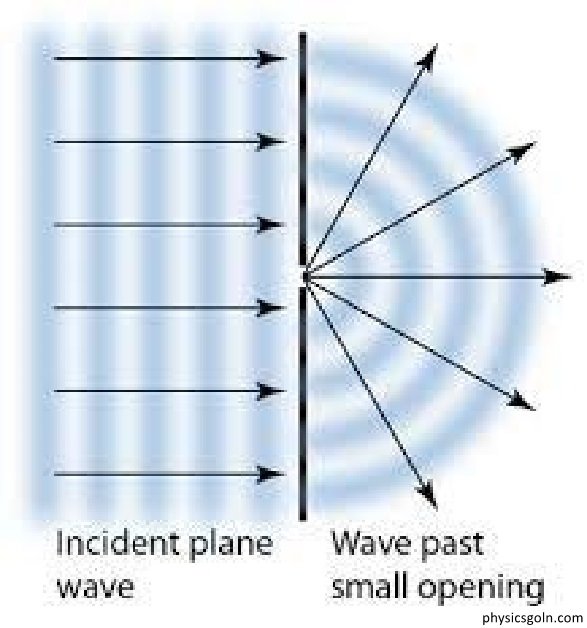
কোনো বিন্দু উৎস বা ক্ষুদ্র ছিদ্র থেকে আলোক তরঙ্গ চারিদিকে ছড়িয়ে পড়লে যে তরঙ্গমুখ অগ্রসর হয় সেটি গোলাকার তরঙ্গমুখ।
(খ) চোঙাকৃতি তরঙ্গমুখ:
কোনো রেখা থেকে বা চিড় থেকে আলোক তরঙ্গ চারিদিকে ছড়িয়ে পড়লে যে তরঙ্গমুখ অগ্রসর হয় সেটি চোঙাকৃতি তরঙ্গমুখ। কারণ কোনো রেখা উৎস থেকে সমদূরত্বে অবস্থিত বিন্দুগুলো একটি চোঙের তলে অবস্থান করে।
(গ) সমতল তরঙ্গমুখ:
অসীমে অবস্থিত উৎস থেকে যে রশ্মিগুলো আসে সেগুলো সমাাল হওয়ায় এর তরঙ্গমুখ সমতল হয়। ফলে সমতল তরঙ্গমুখ সৃষ্টি হয়।
তরঙ্গমুখের বৈশিষ্ট (Properties of Wavefront):
তরঙ্গমুখের কতকগুলি বৈশিষ্ট আছে, তা নীচে দেয়া হলো।
১। তরঙ্গমুখের যেকোনো বিন্দুতে অঙ্কিত অভিলম্ব ঐ বিন্দুতে তরঙ্গের বেগের দিক নির্দেশ করে।
২। কোনো তরঙ্গের বেগ বলতে প্রকৃত পক্ষে তরঙ্গমুখের বেগকে বোঝায়। অর্থাৎ, তরঙ্গের বেগ v হলে তরঙ্গমুখের বেগও v
৩। তরঙ্গমুখ সমতল বা গোলীয় যাই হোক না কেন,পরস্পর দুটি সমদশা সম্পন্ন তরঙ্গমুখের লম্ব দূরত্বকে ঐ তরঙ্গের তরঙ্গদৈর্ঘ্য বলে।
৪। একই তরঙ্গমুখের উপর অবস্থিত যে কোনো দুটি বিন্দুর মধ্যে দশা পার্থক্য সর্বদাই শূন্য।
হাইগেন্সের নীতি(Huygens’ Principles):
ডাচ বিজ্ঞানী ক্রিস্টিয়ান হাইগেন্স (Christian Huygens) ১৬৭৮ সালে তরঙ্গমুখের সঞ্চালন বিষয়ে একটি জ্যামিতিক পদ্ধতির অবতারণা করেন। তার এই পদ্ধতি প্রয়োগ করলে আলেকের প্রতিফলন, প্রতিসরণ, ব্যাতিচার, অপবর্তন ইত্যাদি খুব সহজেই ব্যাখ্যা করা যায় এবং অনুভব করা যায়। অর্থাৎ আলোকীয় ঘটনাগুলো ব্যাখ্যার জন্য খুব উপযোগী।
হাইগেন্সের নীতির সাহায্যে একটি তরঙ্গমুখের আকৃতি ও অবস্থান থেকে পরবর্তী তরঙ্গমুখের আকৃতি ও অবস্থান খুব সহজেই নির্ণয় করা যায়।
হাইগেন্সের নীতি ঃ
একটি তরঙ্গমুখের উপর অবস্থিত প্রতিটি বিন্দু এক একটি আন্দোলনের ক্ষুদ্র উৎস (গৌণ উৎস) এবং ঐ বিন্দুগুলো থেকে গৌণ তরঙ্গমালা নির্গত হয়ে একই বেগে চারিদিকে ছড়িয়ে পড়ে। এ সব গৌণ তরঙ্গমালা সম্মুখ দিকে মোড়ক বিবেচনা করলে বা ঐ সব তরঙ্গমালার সম্মুখ দিক স্পর্শ করে একটি তল অঙ্কন করলে তরঙ্গ মুখের নতুন অবস্থান পাওয়া যায়। এটিই হাইগেন্সের নীতি।
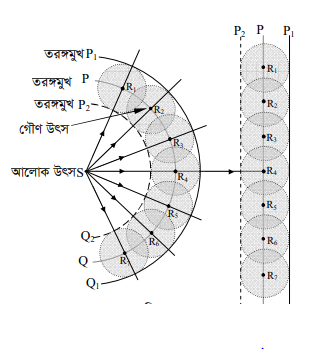
ব্যাখ্যা ঃ
চিত্রে হাইগেন্সের নীতি দেখানো হলো। হাইগেন্সের নীতি অনুসারে উৎস থেকে আলো আড় তরঙ্গ আকারে ইথার মাধ্যমের ভিতর দিয়ে চারিদিকে । সময় পর ছড়িয়ে পড়ে। আলোর বেগ c হয় তবে ‘ সময়ে S উৎস থেকে উৎপন্ন তরঙ্গ ct’ দূরত্ব অতিক্রম করবে। সুতরাং S উৎস থেকে ct’ এর সমান ব্যাসার্ধ নিয়ে একটি PQ গোলক অঙ্কণ করলে গোলকের উপর সমদশা সম্পন্ন বিন্দুর সঞ্চার পথকে তরঙ্গমুখ বলে (চিত্র ৭.৩)।
হাইগেন্সের নীতি অনুসারে তরঙ্গমুখের প্রতিটি বিন্দু R1, R2, R3, R4, R5, R, এক একটি গৌণ উৎস হিসাবে কাজ করে এবং সেখান থেকে গোলীয় অনুতরঙ্গ চারিদিকে প্রসারিত হতে শুর করে। এখন, সময় পর গৌণ উৎস থেকে উৎপন্ন তরঙ্গ ct দূরত্ব অতিক্রম করবে। সুতরাং, R1, R2, R3, R4 R3, Rg প্রতিটি গৌণ উৎস থেকে ct এর সমান ব্যাসার্ধ নিয়ে এক একটি গোলক কল্পনা করলে R1,R2, R3, R4, R, R, বিন্দু থেকে অনুতরঙ্গগুলো । সময় পরে গোলকগুলোর উপরিতলে পৌঁছাবে।
হাইগেনসের নীতি অনুসারে ছোট ছোট গোলকগুলোর সামনের দিকের স্পর্শতল PQ হবে। সময় পর সামনের দিকে এগিয়ে যাওয়া তরঙ্গমুখ। মনে রাখতে হবে P,Q, গোলীয় তরঙ্গমুখের কেন্দ্র s।
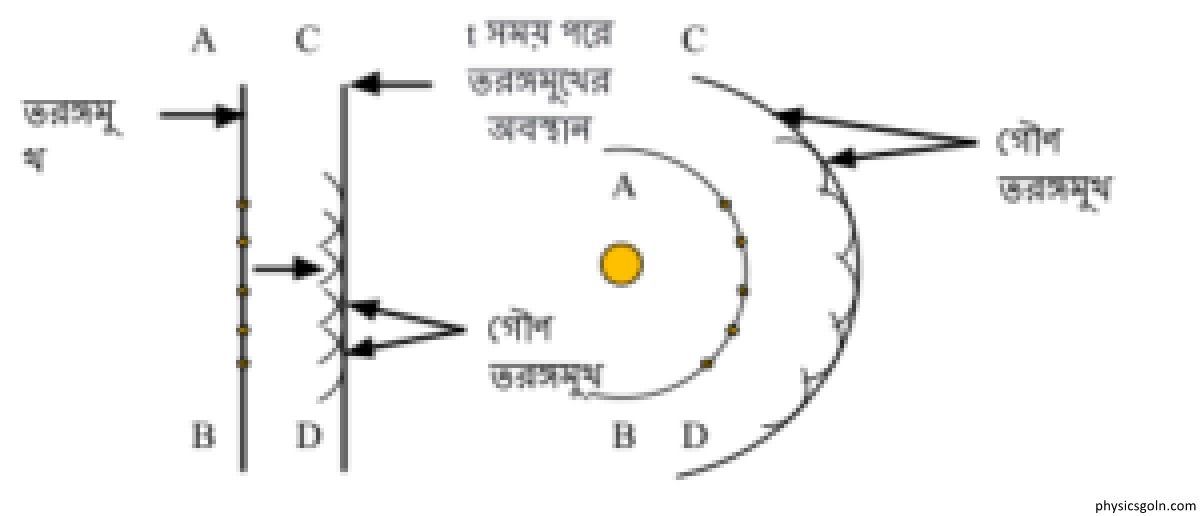
আলোক উৎস অর্থাৎ কেন্দ্র থেকে তরঙ্গমুখের দূরত্ব খুব বেশী না হলে তরঙ্গমুখ গোলীয় হয় (চিত্র ৭.৩) এবং আলোক উৎস অর্থাৎ কেন্দ্র থেকে তরঙ্গমুখের দূরত্ব খুব বেশী হলে তরঙ্গমুখকে সমতল ধরা হয়।
হাইগেন্সের অঙ্কণ পদ্ধতি থেকে দেখা যায় যে, PQ তরঙ্গমুখের পিছনে P, Q, তরঙ্গমুখের মত P, Q, তরঙ্গমুখ পাওয়া যায়, যাকে পশ্চাদ্বর্তী তরঙ্গমুখ বলা যেতে পারে। হাইগেন্সের মতে পশ্চাদ্বর্তী তরঙ্গমুখের কোনো অস্তিত্ব নাই। তার এই বক্তব্যের তাত্ত্বিক এবং পরীক্ষণমূলক প্রমাণ পরে পাওয়া গেছে।
সার-সংক্ষেপ :
তরঙ্গমুখ:
কোনো উৎস থেকে তরঙ্গ যখন শূন্য বা কোনো মাধ্যমে মধ্য দিয়ে সঞ্চালিত হয় তখন শূন্য বা কোনো মাধ্যমের বিন্দুগুলো কম্পিত হতে থাকে। যেকোনো মুহূর্তে একই দশা সম্পন্ন বিন্দুগুলো যে রেখার বা তলের উপর অবস্থিত থাকে তাকে তরঙ্গমুখ বলে ।
গোলীয় তরঙ্গমুখ:
কোনো বিন্দু উৎস বা ক্ষুদ্র ছিদ্র থেকে আলোক তরঙ্গ চারিদিকে ছড়িয়ে পড়লে যে তরঙ্গমুখ অগ্রসর হয় সেটি গোলাকার তরঙ্গমুখ।
চোঙাকৃতি তরঙ্গমুখ:
কোনো রেখা থেকে বা চিড় থেকে আলোক তরঙ্গ চারিদিকে ছড়িয়ে পড়লে যে তরঙ্গমুখ অগ্রসর হয় সেটি চোঙাকৃতি তরঙ্গমুখ। কারণ কোনো রেখা উৎস থেকে সমদূরত্বে অবস্থিত বিন্দুগুলো একটি চোঙের তলে অবস্থান করে।
সমতল তরঙ্গমুখ:
অসীমে অবস্থিত উৎস থেকে যে রশ্মিগুলো আসে সেগুলো সমাাল হওয়ায় এর তরঙ্গমুখ সমতল | হয়। ফলে সমতল তরঙ্গমুখ সৃষ্টি হয়।
হাইগেন্সের নীতি:
একটি তরঙ্গমুখের উপর অবস্থিত প্রতিটি বিন্দু এক একটি আন্দোলনের ক্ষুদ্র উৎস (গৌণ উৎস) এবং ঐ বিন্দুগুলো থেকে গৌণ তরঙ্গমালা নির্গত হয়ে একই বেগে চারিদিকে ছড়িয়ে পড়ে। এ সব গৌণ তরঙ্গমালা সম্মুখ | দিকে মোড়ক বিবেচনা করলে বা ঐ সব তরঙ্গমালার সম্মুখ দিক স্পর্শ করে একটি তল অঙ্কন করলে তরঙ্গ মুখের নতুন অবস্থান পাওয়া যায়। এটিই হাইগেন্সের নীতি ।
বহুনির্বাচনী প্রশ্নঃ
১। কোনটি আলোর তরঙ্গমুখ নয়?
ক. গোলীয় তরঙ্গমুখ
খ. সমতল তরঙ্গমুখ
গ. চোঙাকৃতি তরঙ্গমুখ
ঘ. রৈখিক তরঙ্গমুখ
২। তরঙ্গমুখের বৈশিষ্ট হিসাবে বলা যায়,
i. তরঙ্গমুখের কোনো বিন্দুতে অঙ্কিত অভিলম্ব ঐ বিন্দুতে তরঙ্গের বেগের দিক নির্দেশ করে।
ii. পরস্পর দুটি সমদশা সম্পন্ন তরঙ্গমুখের লম্ব দূরত্বকে ঐ তরঙ্গের তরঙ্গদৈর্ঘ্য বলে।
iii. একই তরঙ্গমুখের উপর অবস্থিত যে কোনো দুটি বিন্দুর মধ্যে দশা পার্থক্য সর্বদাই শূন্য।
কোনটি সঠিক?
ক. i ও ii
খ. ii ও iii
গ. i ও iii
ঘ. i, ii ও iii.
