দৈর্ঘ্য ও সময়ের আপেক্ষিকতা : দৈর্ঘ্য সংকোচন, কাল দীর্ঘায়ন

আজকে আমরা দৈর্ঘ্য ও সময়ের আপেক্ষিকতা : দৈর্ঘ্য সংকোচন, কাল দীর্ঘায়ন সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৮ এর  আধুনিক পদার্থবিজ্ঞান এর অন্তর্ভুক্ত।

দৈর্ঘ্য ও সময়ের আপেক্ষিকতা : দৈর্ঘ্য সংকোচন, কাল দীর্ঘায়ন

আপেক্ষিক তত্ত্ব অনুসারে দৈর্ঘ্য ও সময়ের আপেক্ষিকতা

লরেঞ্জ রূপার বিধি অনুসারে, স্থানাঙ্ক এবং সময়াঙ্ক জড় কাঠামোর আপেক্ষিক বেগের উপর নির্ভরশীল। সুতরাং দৈর্ঘ্য এবং সময় পরম হতে পারে না। দৈর্ঘ্য ও সময়ের আপেক্ষিকতার বিষয়গুলো আইনস্টাইনের বিশেষ আপেক্ষিক তত্ত্বের সাহায্যে ব্যাখা করা যায়।

দৈর্ঘ্য সংঙ্কোচন (Length contraction):

কোনো বস্তুর দৈর্ঘ্যের পরিমাপ সকল কাঠামোতে সমান নয় অর্থাৎ দৈর্ঘ্যের পরিমাপ পরম নয়। এর দৈর্ঘ্য পর্যবেক্ষক ও বস্তুর মধ্যে আপেক্ষিক গতির উপর নির্ভরশীল। সুতরাং কোনো বস্তুর দৈর্ঘ্যের পরিমাপ আপেক্ষিক।

গতিশীল কাঠামোতে অবস্থিত কোন দন্ডের (কাঠামোর গতির দিক বারাবর) দৈর্ঘ্য স্থির কাঠামোতে অবস্থিত পর্যবেক্ষক পরিমাপ করলে তার দৈর্ঘ্য ছোট হয়। একে দৈর্ঘ্য সংঙ্কোচন বলে।

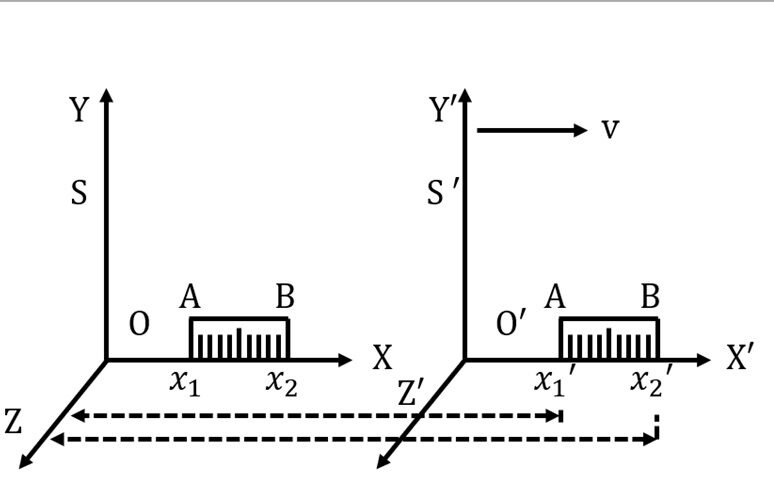
S এবং S’ দুটি কাঠামো বিবেচনা করি [চিত্র]। এখানে s কাঠামো স্থির এবং S’ কাঠামো গতিশীল। স্থির অবস্থায় একটি দ AB বিবেচনা করি, যা s কাঠামোর X অক্ষ বরাবর রাখা আছে। এ কাঠামোর একজন পর্যবেক্ষক দটির দু’প্রান্তের স্থানাঙ্ক নির্ণয় করলেন x1 এবং x2 । যেহেতু s কাঠামো স্থির সূতরাং স্থির কাঠামোতে দীটির দৈর্ঘ্য,

S’ কাঠামো S কাঠামো সাপেক্ষে। ধ্রুব বেগে গতিশীল। এখন একজন পর্যবেক্ষক একই সময়ে S কাঠামোর AB দরে দু’প্রান্জের স্থানাঙ্ক নির্ণয় করলেন x’1 এবং x’2। সুতরাং S’ কাঠামোতে দটির দৈর্ঘ্য, L = x’2 – x’1

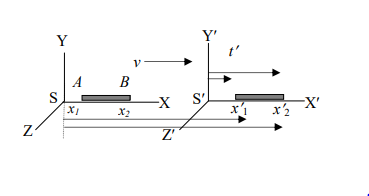
অতএব, লরেঞ্জ-এর বিপরীত রূপান্ডু বিধি অনুসারে x1 এবং x2 এর সাথে x’1 এবং x’2 এর সম্পর্ক হলো,

x₁ = (x’1 + vt)/√(1 – v2/c2)  এবং x2 = (x’2 + vt)/√(1 – v2/c2)

এখন উপরের সমীকরণ x2 থেকে x1 বিয়োগ করে পাই-

x2 – x₁ = (x’2 + vt)/√(1 – v2/c2) – (x’1 + vt)/√(1 – v2/c2)

বা, Lo = (x’2  – x’1)/√(1 – v2/c2)      [:: L = x2 −x1]

বা,  L/√(1 – v2/c2)         [:: L = x2 – x]

বা, L = Lo/√(1 – v2/c2)    ………………………(1)

যেহেতু বস্তুর বেগ কখনই আলোর বেগ অপেক্ষা বেশী বা সমান হতে পারেনা সেহেতু v2/c2 <1

অতএব, √(1-v2/c2) <1 তাই L<Lo। অর্থাৎ স্থির জড় প্রসঙ্গ কাঠামো থেকে পরিমাপকৃত গতিশীল জড় প্রসঙ্গ কাঠামোর কোনো বস্তুর দৈর্ঘ্য (গতিশীল জড় প্রসঙ্গ কাঠামোটি যে অক্ষ বরাবর গতিশীল সেই অক্ষ বরাবর অবস্থিত বস্তু)

স্থির জড় প্রসঙ্গ কাঠামোতে অবস্থিত বস্তুর দৈর্ঘ্য অপেক্ষা ছোট হয়। যদি v<<c হয় তবে v2/c2 ≈ 0, সেক্ষেত্রে L = Lo হবে। অর্থাৎ সাধারণ বেগে গতিশীল বস্তুর ক্ষেত্রে দৈর্ঘ্য সংকোচন পরিলক্ষিত হয় না। বস্তুর বেগ যতই আলোর বেগের নিকটবর্তী হবে দৈর্ঘ্য তত বেশী সংকুচিত হবে।

কাল দীর্ঘায়ণ (Time Dilation)

সময়ের পরিমাপ সকল কাঠামোতে সমান নয় অর্থাৎ সময়ের পরিমাপ পরম নয়। দুটি জড় প্রসঙ্গ কাঠামোর মধ্যে যদি আপেক্ষিক গতি থাকে তবে এই দুই কাঠামোতে অবস্থিত দুইজন পর্যবেক্ষকের নিকট সংঘটিত দুটি ঘটনার মধ্যবর্তী সময়ের ব্যবধান সমান হবে না। স্থির জড় প্রসঙ্গ কাঠামোর পর্যবেক্ষকের নিকট সময়ের ব্যবধান গতিশীল জড় প্রসঙ্গ কাঠামোর পর্যবেক্ষকের নিকট সময়ের ব্যবধান অপেক্ষা বেশী হয়।

গতিশীল কাঠামোতে অবস্থিত কোনা ঘড়িতে পরিমাপকৃত কোনো ঘটনার সময়কাল, স্থির কাঠামোতে অবস্থিত পর্যবেক্ষকের নিকট দীর্ঘ হয়। একে কাল দীর্ঘায়ণ বা সময় প্রসারণ বলে । মনে করি, S স্থির কাঠামোতে একজন পর্যবেক্ষক $ আলোক উৎস থেকে একটি আলোক রশ্মি । Z উচ্চতায় অবস্থিত একটি দর্পণে প্রতিফলিত করে d গ্রাহক যন্ত্রে আপতিত হবার সময় নিরূপণ করছেন।

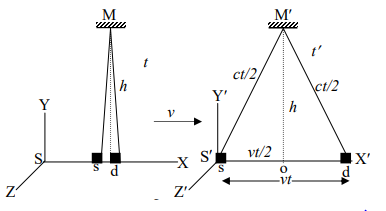
একই পরীক্ষণ যদি X-অক্ষ বরাবর ” ধ্রব বেগে গতিশীল SM কাঠামোর পর্যবেক্ষক সম্পন্ন করেন তবে তার ঘড়িতে যে সময় পরিমাপ করবেন তা S স্থির কাঠামোতে পরীক্ষার সময় এই কাঠামোতে অবস্থিত ঘড়িতে যে সময় (tg) দেখিয়েছে তার সংখ্যা মানের সমান (বিশেষ আপেক্ষিক তত্ত্বের প্রথম স্বীকার্য অনুসারে)। গতিশীল S’ কাঠামোর পর্যবেক্ষকের পরীক্ষা সম্পন্ন করতে যদি ‘ সময় লাগে তবে, 2h=ct’

বা, 2h = cto

কারণ t’ = to ( বিশেষ আপেক্ষিক তত্ত্বের প্রথম স্বীকার্য অনুসারে)

বা, 4h2 = c2to2 .………………………(2)

এখন যদি স্থির কাঠামোর পর্যবেক্ষক গতিশীল কাঠামোর পরীক্ষণীয় ঘটনাটি পর্যবেক্ষণ করেন তবে

তিনি ভিন্ন চিত্র দেখবেন। কারণ আলোক উৎস s হতে দর্পণে যেতে ও d গ্রাহক যন্ত্রে আসতে যে সময় লাগে যে সময়ে কাঠামোটি vt দূরত্ব অতিক্রম করবে। ফলে তিনি আলোর গমন পথ sM’d দেখবেন। পিথাগোরাসের সূত্রানুসারে, sM’2 = h2 + Os2

যদি স্থির কাঠামোর পর্যবেক্ষকের নিকট এই সময় t মনে হয় তবে,

মান বসালে, (ct/2)2 = h2 + (vt/2) 2

বা, c2t2/4 – v2t2/4 = h2

বা, t2(c2 −v2) = 4h2 .………………………(3)

(3) নং সমীকরণে (2) নং সমীকরণের মান বসিয়ে, t2(c2 −v2) = c2to2

বা, t2 = c2to2/(c2 −v2)

বা, t2 = c2to2/c²(1-v²/c²)

বা, t = to/(1-v²/c²) ………………………(4)

যেহেতু বস্তুর বেগ কখনই আলোর বেগ অপেক্ষা বেশী বা সমান হতে পারেনা সেহেতু, v²/c² <1

অতএব, √(1 – v2/c2) <1 তাই t>to। অর্থাৎ স্থির জড় প্রসঙ্গ কাঠামো থেকে পরিমাপকৃত সময়ের ব্যবধান গতিশীল জড় প্রসঙ্গ কাঠামোর সময়ের ব্যবধান অপেক্ষা দীর্ঘ। যদি v<< c হয় তবে v²/c² ≈ 0, সেক্ষেত্রে t = to হবে। অর্থাৎ সাধারণ বেগে গতিশীল হলে উভয় ক্ষেত্রেই সময়ের ব্যবধান সমান। গতিশীল জড় প্রসঙ্গ কাঠামোর বেগ যতই আলোর বেগের নিকটবর্তী হবে সময়ের ব্যবধান তত বেশী হবে।

উদাহরণ ১:

একটি রকেট কত বেগে চললে এর চলমান দৈর্ঘ্য নিশ্চল দৈর্ঘ্যের অর্ধেক হবে?

সমাধান :

দেয়া আছে, L = Lo/2 এবং v = ?

দৈর্ঘ্যের আপেক্ষিকতা থেকে আমরা জানি, L = Lo√(1 – v2/c2)

বা, (L/Lo)2 = (1 – v2/c2) 

 বা,  v2/c2 = 1- (L/Lo)2

বা, v = c[1-(L/Lo)2]1/2

মান বসালে, v = 3 × 108 × [ 1 – (Lo/2Lo)2]1/2 =  3×108×(1-1/4)1/2  =3×108×(3/4)1/2  =3×108×0.866

বা, v = 2.598×10 m

উ: v =  2.598x108m

উদাহরণ ২:

একটি মেসন কণার গড় আয়ু 3×10s । যদি কণাটি 0.85c বেগে গতিশীল হয় তবে এর গড় আয়ু বের করন।

সমাধান :

দেয়া আছে, to = 3×10^8s, v = 0.85c এবং t = ?

সময়ের আপেক্ষিকতা থেকে আমরা পাই, t = to/√(1 – v2/c2)

মান বসালে, t = 3×10-8s/√(1 – (0.85c)2/c2) =  (3×10-8s)/√1-0.7225 = 5.69×10-8s

উ: 5.69 ×10″ s S

উদাহরণ ৩:

25 বছর বয়সের একজন মহাশূন্যচারী মহাকাশযানে 1.8×10 ms-1 বেগে চলে 30 বছর পর ফিরে এলেন। তাঁর বর্তমান বয়স কত?

সমাধান :

দেয়া আছে, v=1.8×10 ms-1, t = 30y,to = ? এবং ভ্রমনের শেষে বয়স, 25 + t0 = ?

মহাশূন্যচারীর বয়স বৃদ্ধি হলে সময়ের আপেক্ষিকতা থেকে আমরা পাই, to

t =  to/√(1 – v2/c2)

বা, to =  t/√(1 – v2/c2)

মান বসালে, to = 30√{1-(1.8 x108 ) 2 /(3×108)2 = 30 x √0.64 = 24y

সুতরাং মহাশূন্যচারীর বর্তমান বয়স 25 + 24 = 49y

উ: 49y

সার-সংক্ষেপ :

আপেক্ষিক তত্ত্ব অনুসারে দৈর্ঘ্য ও সময়ের আপেক্ষিকতা

লরেঞ্জ রূপান্ডু বিধি অনুসারে, স্থানাঙ্ক এবং সময়াঙ্ক জড় কাঠামোর আপেক্ষিক বেগের উপর নির্ভরশীল। সুতরাং দৈর্ঘ্য এবং সময় পরম হতে পারে না। দৈর্ঘ্য ও সময়ের আপেক্ষিকতার বিষয়গুলো আইনস্টইনের বিশেষ আপেক্ষিক তত্ত্বের
সাহায্যে ব্যাখ্যা করা যায় ।

দৈর্ঘ্য সংঙ্কোচন:

কোনো বস্তুর দৈর্ঘ্যের পরিমাপ সকল কাঠামোতে সমান নয় অর্থাৎ দৈর্ঘ্যের পরিমাপ পরম নয়। এর | দৈর্ঘ্য পর্যবেক্ষক ও বস্তুর মধ্যে আপেক্ষিক গতির উপর নির্ভরশীল। সুতরাং কোনো বস্তুর দৈর্ঘ্যের পরিমাপ আপেক্ষিক।
L=Lo√1-v²/c²

কাল দীর্ঘায়ণ:

সময়ের পরিমাপ সকল কাঠামোতে সমান নয় অর্থাৎ সময়ের পরিমাপ পরম নয়। দুটি জড় প্রসঙ্গ | কাঠামোর মধ্যে যদি আপেক্ষিক গতি থাকে তবে এই দুই কাঠামোতে অবস্থিত দুইজন পর্যবেক্ষকের নিকট সংঘটিত দুটি ঘটনার মধ্যবর্তী সময়ের ব্যবধান সমান হবে না। t = to √1-v2/c²

বহুনির্বাচনী প্রশ্নঃ

১। নীচের কোনটি দৈর্ঘ্য সংঙ্কোচন ও কাল দীর্ঘায়ণে সমীকরণ?

ক. L = Lo√(1 – v2/c2) 3 t =  to√(1 – v2/c2)

খ. L = Lo√(1 – v2/c2) ও to=t/√(1 – v2/c2)

গ. L = Lo√(1 – v2/c2) ও t = to√(1 – v2/c2)

ঘ. L = Lo√(1 – v2/c2)  ও  to=t√(1 – v2/c2)

২। কত বেগে গতিশীল হলে কোনো বস্তুর দৈর্ঘ্য তার মূল দৈর্ঘ্যের এক চতুর্থাংশ হবে?

ক. √15/4c

খ. 15/4c

গ. 3/2 C

ঘ.√3/2C