আজকে আমরা কালো বস্তুর বিকিরণ : পণ্ঢ্যাঙ্ক এর কোয়ান্টাম তত্ত্ব সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৮ এর আধুনিক পদার্থবিজ্ঞান এর অন্তর্ভুক্ত।
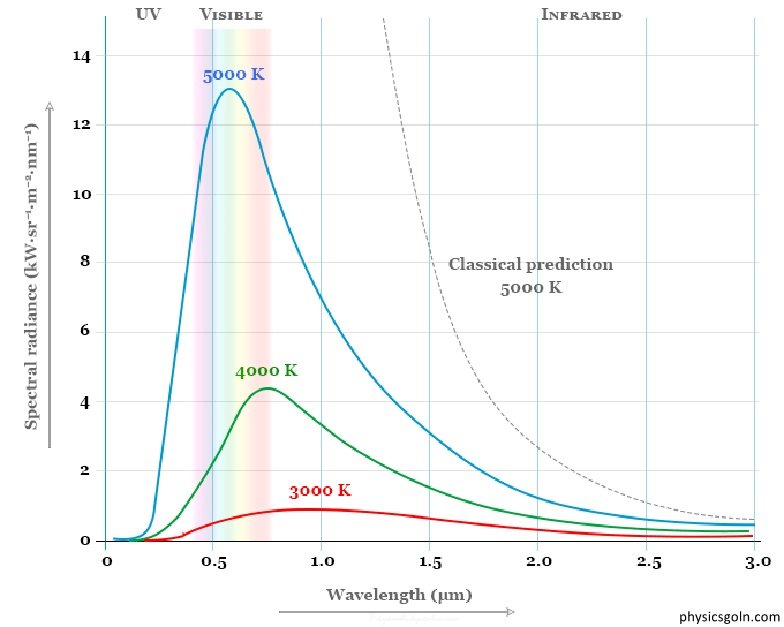
কালো বস্তুর বিকিরণ : পণ্ঢ্যাঙ্ক এর কোয়ান্টাম তত্ত্ব
কৃষ্ণ বস্তুর বিকিরণ (Black Body Radiation):
যে বস্তু এর উপর আপতিত সকল তরঙ্গ দৈর্ঘ্যের তাড়িতচৌম্বক বিকিরণ শোষন করে অর্থাৎ কোন প্রতিসরণ বা প্রতিফলন হয় না তাকে কৃষ্ণ বস্তু বলে। কৃষ্ণ বস্তু থেকে সকল কম্পাংকের বিকিরণ সুষম ভাবে নিঃসরণ করে। কৃষ্ণ বস্তু যে বিকিরণ নিসঃরণ করে তাকে কৃষ্ণ বস্তুর বিকিরণ বলে। কৃষ্ণ বস্তু একটি আদর্শ বিকিরক। প্রকৃত পক্ষে কৃষ্ণ বস্তু একটি আদর্শগত ধারণা। এমন কোনো পৃষ্ঠ নাই যা আদর্শ কৃষ্ণ বস্তুর ন্যায় আচরণ করে। প্রদীপের কালি আপতিত বিকিরণের ৯৬% শোষণ করে। পশ্চাটিনামের কালি আপতিত বিকিরণের ৯৮% শোষন করে।
১৮৫৮ সালে কার্শপ (Kirchoff) কৃষ্ণ বস্তু সম্পর্কে দুটি সূত্র আবিস্কার করেন। সূত্র দুটি হলোঃ-
১) একটি কৃষ্ণ বস্তুকে তাপ দিলে শুধু যে তার উপর আপতিত সকল বিকিরণ সম্পূর্ণভাবে শোষণ করে তা নয়, কৃষ্ণবস্তুটি একটি আদর্শ বিকিরক হিসাবে কাজ করে।
২) কোনো কৃষ্ণবস্তু থেকে নিঃসরিত বিকিরণ কৃষ্ণবস্তুকে যে তাপ মাত্রায় উন্নীত করা হয় তার উপর নির্ভরশীল, বস্তুর প্রকৃতি ও উপাদানের উপর নির্ভশীল নয়।
স্থির তাপমাত্রায় বিভিন্ন তরঙ্গ দৈর্ঘ্যের বিকিরণের নিসঃরণ শক্তির বন্টন হিসাব নিকাশ করার সময় কৃষ্ণ বস্তুকে নির্দিষ্ট তাপমাত্রায় উত্তপ্ত করা হয় এবং অবলোহিত স্পেক্ট্রোমিটারের সাহায্যে বিকিরিত বিভিন্ন তরঙ্গ দৈর্ঘ্যের প্রাবল্য মাপা হয়। কোনো বস্তুর তাপমাত্রা বাড়াতে থাকলে এর রং পরিবর্তিত হয়। এর অর্থ হলো বস্তুর তাপমাত্রা বাড়াতে থাকলে বস্তু থেকে নির্গত বিকিরণের তরঙ্গ দৈর্ঘ্য পরিবর্তিত হতে থাকে। উচ্চ তাপমাত্রায় কম তরঙ্গ দৈর্ঘ্য বিশিষ্ট বিকিরণ বেশী ঘটে।
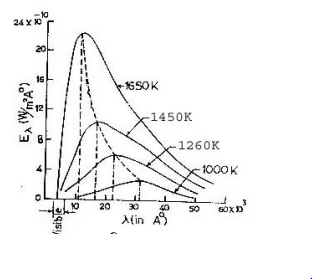
১৮৯৯ সালে লুমার এবং প্রিংসিম (Lumar and Pringsheim) যে পরীক্ষালব্ধ ফলাফল পান তা নিম্নে দেখানো হলো। এই লেখচিত্রে কালো বস্তুর 100K থেকে 1650K তাপমাত্রা পর্যন্ত্ দেখানো হয়েছে। Y-অক্ষে বিকিরণ ক্ষমতা Eλ এবং X- অক্ষে তরঙ্গ দৈর্ঘ্য λ নির্দেশ করছে।
λ এবং λ+dλ তরঙ্গ দৈর্ঘ্যের মধ্যে প্রতি একক ক্ষেত্রফল থেকে প্রতি সেকেন্ডে বিকিরণ শক্তির পরিমানকে Exda দিয়ে নির্দেশ করা হয়।
সুতরাং বিকিরণ ক্ষমতা = λ এবং λ+dλ তরঙ্গ দৈর্ঘ্যের মধ্যে প্রতি একক ক্ষেত্রফল থেকে প্রতি সেকেন্ডে বিকিরণ শক্তির পরিমান/
তরঙ্গ দৈর্ঘ্যের পার্থক্য dλ
লেখচিত্র থেকে নিম্নলিখিত সিদ্ধান্দ্রে উপনিত হওয়া যায়।
১) তাপমাত্রা বৃদ্ধির সাথে সাথে প্রতি তরঙ্গ দৈর্ঘ্যের E বৃদ্ধি পায়।
২) স্থির তাপমাত্রায় নির্দিষ্ট তরঙ্গ দৈর্ঘ্য λm (স্থির তাপমাত্রায় বিকিরণের যে তরঙ্গ দৈর্ঘ্য সর্বোচ্চ শক্তি বিকিরণ করে তাকে λm বলে) অতিক্রম না হওয়া পর্যড্ তরঙ্গ দৈর্ঘ্য বৃদ্ধির সাথে সাথে Eλ বৃদ্ধি পায় এবং λm অতিক্রম করার পর λ বৃদ্ধির সাথে সাথে Eλ হ্রাস পেতে থাকে অর্থাৎ সর্বোচ্চ Eλ মানের জন্য যে λm পাওয়া যায় তা তাপমাত্রা বৃদ্ধির সাথে সাথে ছোট তরঙ্গ দৈর্ঘ্যের দিকে স্থানাড্ররিত হয়।
লুমার এবং প্রিংসিম এর পরীক্ষা লব্ধ ফলাফল থেকে ভীন (Wien) কৃষ্ণ বস্তুর এ সংক্রাড় সূত্র প্রদান করেন যা ভীনের সরণ সূত্র নামে পরিচিত।
সূত্র ঃ-
কোন কৃষ্ণ বস্তু থেকে যে তরঙ্গ দৈর্ঘ্যের সর্বোচ্চ পরিমাণ শক্তি বিকিরণ করে তা তার পরম তাপমাত্রার ব্যড় ানুপাতিক ।
অর্থাৎ λm ∝ 1/T
বা, λmT = k ………………..(1)
এখানে k একটি সমানুপাতিক ধ্রুবক। এর পরীক্ষলব্ধ মান 2.9×10-3mK
১৮৯৬ সালে ভীন কৃষ্ণ বস্তুর বিকিরণ নিঃসরণের জন্য নিম্নোক্ত ঐচ্ছিক ধারণা (arbitary assumption) উপস্থাপন করেন,
১) কৃষ্ণ বস্তু রূপে বিবেচিত ফাঁপা গোলকটির অভ্যস্থ বিকিরণ, আণবিক পালণ্ঢার (Molecular dimension) ছন্দিত স্পন্দনের জন্য সৃষ্টি হয়।
২) বিকিরণ নিঃসরণের কম্পাংক হলো ছন্দিত স্পন্দনের গতিশক্তির সমানুপাতিক ।
৩) নির্দিষ্ট কোনো তরঙ্গের বিকিরণের প্রাবল্য সেই তরঙ্গ দৈর্ঘ্যের উপযোগী ছন্দিত স্পন্দনের সংখ্যার সমানুপাতিক । এই ধারণার ভিত্তিতে নিম্নোক্ত সমীকরণ প্রতিষ্ঠা করেন,
Eλdλm = (C1/λ5e ^C2/λT)dλ ………………..(2)
এখানে C1 এবং C2 ঐচ্ছিক ধ্রুবক, T = পরম তাপমাত্রা ।
এই সূত্রানুসারে ছোট তরঙ্গ দৈর্ঘ্যের ক্ষেত্রে লুমার ও প্রিংসিম পরীক্ষালব্ধ ফলাফলের সাথে সঙ্গতিপূর্ণ হয় কিন্তু খুব বড় তরঙ্গ
দৈর্ঘ্যের ক্ষেত্রে তা সঙ্গতিপূর্ণ হয় না।
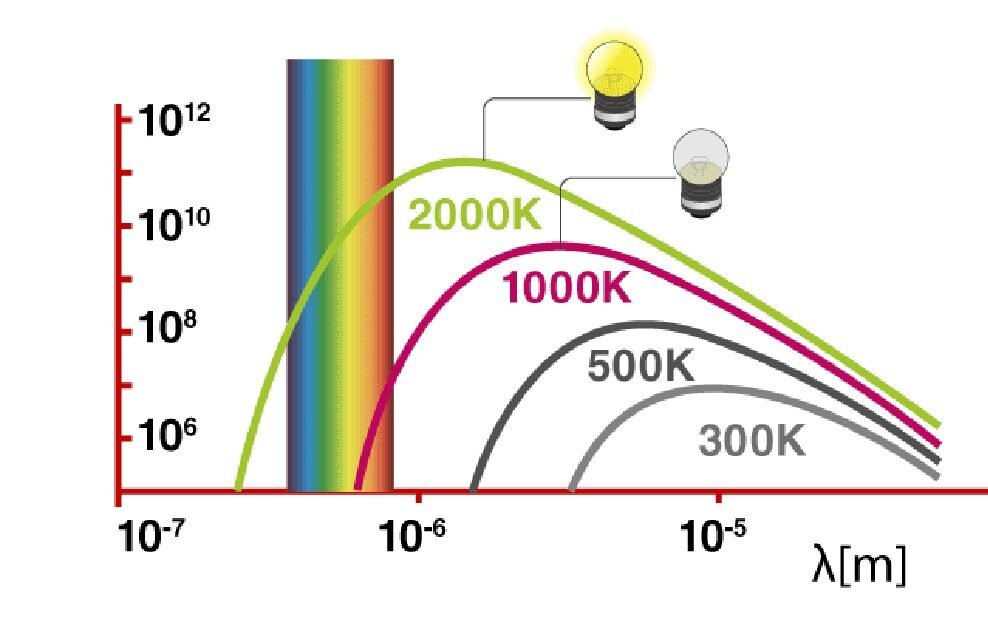
র্যালে-জীন্স ( Rayleigh Jean’s)-এর সূত্র :-
ফাঁপা গোলকে আদর্শ প্রতিফলক তল হিসাবে বিবেচনা করে র্যালে-জীন্স (Rayleigh-Jean’s) একটি সমীকরণ প্রতিষ্ঠা করেন। এই সূত্রানুসারে শক্তি ঘনত্ব Uλdλ অর্থাৎ λ এবং λ+ dλ তরঙ্গদৈর্ঘ্যের সীমানার মধ্যে একক আয়তনের বদ্ধ ক্ষেত্রে শক্তি
Uλdλ = (8πkT/λ4)dλ ………………..(3)
এখানে, k = বোল্টজম্যান ধ্রুবক এবং T = পরম তাপমাত্রা ।
সূত্রটি লুমার এবং প্রিংসিম লেখচিত্রের দীর্ঘ তরঙ্গ দৈর্ঘ্যের সাথে সঙ্গতিপূর্ণ হয় কিন্তু হ্রস্ব তরঙ্গ দৈর্ঘ্যের সাথে মিলে না।
স্টিফেন বোল্টজম্যান (Stefan Boltzmann) সূত্র :-
কোনো কৃষ্ণ বস্তুর একক ক্ষেত্রফল থেকে প্রতি একক সেকেন্ডে যে শক্তি নিসঃরণ করে তা তার পরম তাপমাত্রার
চতুর্থঘাতের সমানুপাতিক ।
কোন কৃষ্ণ বস্তুর একক ক্ষেত্রফল থেকে প্রতি একক সেকেন্ডে যদি E শক্তি নিসঃরণ করে এবং বস্তুটির পরম তাপমাত্রার T
হয় তবে, E ∝ T4
বা, E = ∂T4 ………………..(4)
এখানে ∂ একটি সমানুপাতিক ধ্রুবক। একে স্টিফেনের ধ্রুবক বলে। এর মান 5.7×10-8 Wm-2K-4। স্টিফেনের
সূত্রটি বোল্টজম্যান তাপ গতিবিদ্যার সাহায্যে প্রমাণ করেন সে জন্য একে স্টিফেন বোল্টজম্যান সূত্রও বলা হয়।
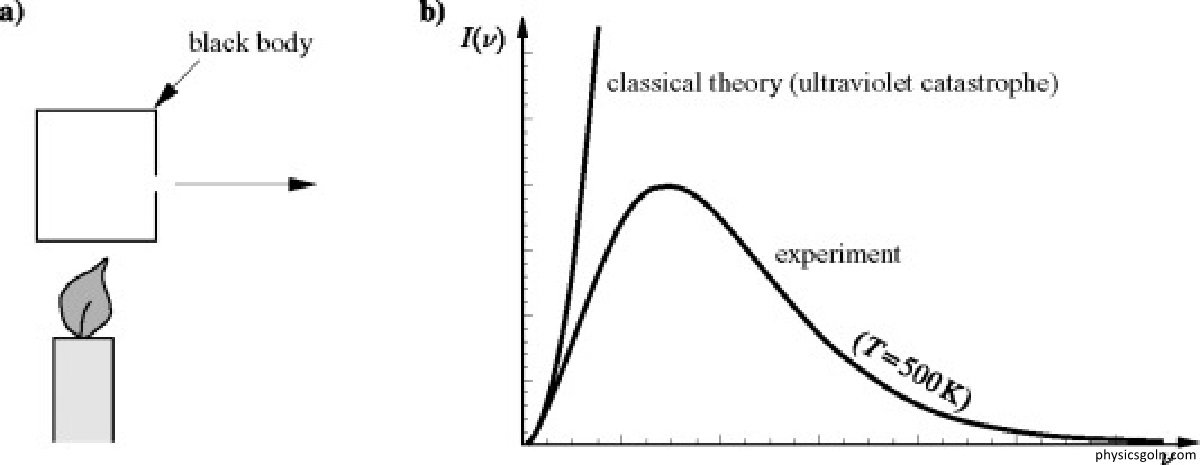
কৃষ্ণ বস্তুর আচরণ ব্যাখ্যায় চিরায়ত বলবিদ্যার ব্যার্থতা
চিরায়ত বলবিদ্যা দ্বারা কৃষ্ণ বস্তুর আচরণ বিভিন্ন ভাবে ব্যাখ্যা করার চেষ্টা করা হয়েছে কিন্তু প্রাপ্ত ফলাফলের সাথে কোনটিই যথাযথ হয়নি।
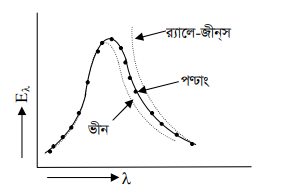
ভীনের সূত্র থেকে পাই, Eλdλ = (C1/λ5e ^C2/λT)dλ
এখানে λ = ∞ হলে Eλ = 0 এবং λ = 0 হলে Eλ = 0 হয়। সুতরাং তরঙ্গ দৈর্ঘ্য শূন্য বা অসীম হলে কোন শক্তির নিঃসরণ হয়না।
আবার T = ∞ হলে Eλ = C1/λ5 হবে যা একটি সসীম মান। কিন্তু পরীক্ষালব্ধ স্টিফেন বোল্টজম্যান সূত্র
E = ∂T4 এর একেবারে বিরোধী (কারণ λ ∝ 1/T তাই Eλ =cT5 যা স্টিফেন বোল্টজম্যান সূত্রের সাথে মিলে না)। তাই এই সিদ্ধান্ত্ ভুল ।
র্যালে-জীসের সূত্র থেকে পাই, Uλdλ = (8πkT/λ4)dλ। এখানে λ = ∞ হলে Uλ = 0 এবং λ = 0 হলে Uλ = ∞ হয়। অর্থাৎ শূন্য তরঙ্গ দৈর্ঘ্যের ক্ষেত্রে এর শক্তি ঘনত্ব অসীম যা অবাস্তব। একে অতিবেগুনী বিপর্যয় বলে।
আবার একক ক্ষেত্রফলে মোট শক্তি
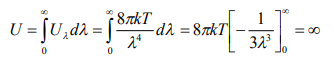
এটাও একটি অবাড়ব মান। কারণ পরীক্ষালব্ধ স্টিফেন বোল্টজম্যান সূত্রানুসারে একটি সসীম মান হবে ।
সুতরাং বলা যায় হ্রস্ব তরঙ্গ দৈর্ঘ্যের ক্ষেত্রে ভীন-এর সূত্র এবং দীর্ঘ তরঙ্গ দৈর্ঘ্যের ক্ষেত্রে র্যালে-জেন্সের সূত্র মোটামুটি প্রযোজ্য হলেও পরীক্ষালব্ধ ফলাফলকে পূর্ণাঙ্গরূপে ব্যাখ্যা করতে চিরায়ত বলবিদ্যা সম্পূর্ণরূপে ব্যর্থ।
ম্যাক্স পণ্ঢ্যাংকের কোয়ান্টাম তত্ত্ব (Quantum Theory of Max Plank):
১৯০১ সালে ম্যাক্স পণ্ঢ্যাংক পূর্ববর্তী বিকিরণের শক্তির অবিচ্ছিন্নতার ধারণা পরিত্যাগ করে এক বৈপণ্ঢবিক অনুকল্প উপস্থাপণ করেন। তার অনুকল্প অনুসারে কৃষ্ণবস্তু স্থির তাপমাত্রায় তাড়িতচৌম্বক তরঙ্গ দ্বারা পূর্ণ থাকে। এই তাড়িতচৌম্বক তরঙ্গগুলো কতকগুলো সরল ছন্দিত স্পন্দক দিয়ে সৃষ্ট। নির্দিষ্ট কম্পাংক বিশিষ্ট সরল ছন্দিত স্পন্দকগুলির নির্দিষ্ট পরিমান শক্তি বিদ্যমান। এই শক্তি তার কম্পাংকের সমানুপাতিক।
যখন সরল ছন্দিত স্পন্দকগুলো তার নিজস্ব কম্পাংকে কাঁপতে থাকে তখন কোনো শক্তি বিকিরণ বা শোষণ করে না। সুতরাং শক্তি অবিচ্ছিন্ন আকারে নির্গত হয়না। বরং অবিছিন্নভাবে অনবরত বালি বা প্যাকেট আকারে নির্গত হয়। বিকিরণ শক্তিকে ক্ষুদ্র ক্ষুদ্র শক্তির প্যাকেটের গুচ্ছ প্রবাহ আকারে বিবেচনা করা হয় । প্রতি প্যাকেট এক একটি কোয়ান্টার বালি। এইজন্য একে পণ্ঢণ্ঢ্যাংকের কোয়ান্টাম তত্ত্ব বলে।
প্রতিটি কোয়ান্টার বােিলর শক্তি E = nhf । এখানে, n = তরঙ্গ সংখ্যা, f =নির্গত তাড়িতচৌম্বক তরঙ্গের কম্পাংক। যেখানে কম্পাংক f = c/λ হলো বিকিরণের তরঙ্গ দৈর্ঘ্য এবং h = 6.626 ×10-34 Js একটি ধ্র“ব সংখ্যা। একে পণ্ঢণ্ঢ্যাংকের ধ্রুবক বলে।
সুতরাং ম্যাক্স পণ্ঢণ্ঢ্যাংকের মতে তাড়িতচৌম্বক তরঙ্গ কোনো অবিছিন্ন তরঙ্গ নয় বরং বিছিন্ন তরঙ্গ এবং প্রতিটি কোয়ান্টা এক একটি অবিভাজ্য একক। প্রতিটি কোয়ান্টা আকার তার বা শক্তি তাড়িতচৌম্বক তরঙ্গের কম্পাংকের উপর নির্ভরশীল। পরে ১৯২৬ সালে লুইস প্রতিটি কোয়ান্টার নাম দেন ফোটন। সুতরাং প্রতিটি ফোটনের শক্তি হলো hf । কোয়ান্টাম তত্ত্বের মূল কথা হলো, তাড়িতচৌম্বক বিকিরণ তরঙ্গধর্মী নয়, বরং এক ধরণের কণার স্রোত, এই কণার নাম ফোটন (Photon)।
এই তত্ত্বানুসারে ম্যাক্স পণ্ঢ্যাংক দেখান যে, f থেকে f+df কম্পাংকের মধ্যে প্রতি একক আয়তনে নিঃসরিত শক্তির পরিমান,
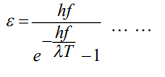
এটাই পণ্ঢণ্ঢ্যাংকের গড় শক্তির রাশিমালা বলে ।
এখানে, k = বোল্টজম্যান ধ্রুবক এবং T = পরম তাপমাত্রা ।
পণ্ঢণ্ঢ্যাংকের প্রকল্প (Plank’s hypothesis) অনুসারে কৃষ্ণ বস্তুর শক্তি বিন্যাসের ব্যাখ্যা পরীক্ষালব্ধ ফলাফলের সাথে সম্পূর্ণরূপে মিলে যায়।
কৃষ্ণ বস্তুর বর্ণালীর শক্তির বন্টন (distribution of energy in the spectrum of black body) যথার্থ ভাবে ব্যাখ্যার মধ্য দিয়েই কোয়ান্টাম বলবিদ্যার যাত্রা শুর”।
কোয়ান্টাম বলবিদ্যার ধারণা পেতে হলে আমাদের ফোটনের ধর্মাবলী জানা প্রয়োজন । নীচে ফোটনের ধর্মগুলো দেয়া হলো।
১। প্রতিটি ফোটন কণাই তড়িৎ নিরপেক্ষ
২। শূন্য মাধ্যমে প্রতিটি ফোটন কণাই আলোর বেগে (c=3×10 ms’) চলাচল করে। কোনো ঘটনাতেই ফোটনের বেগের কোনো হ্রাস বৃদ্ধি ঘটে না।
৩। প্রতি ফোটন দ্বারা বাহিত শক্তির পরিমান E = hf । এখানে f = বিবিরণের কম্পাঙ্ক, h = পণ্ঢ্যাংক ধ্রুবক। ফোটনের স্রোতে ফোটন কণার সংখ্যা যত বেশী হয়, বাহিত শক্তির পরিমাণও তত বেশী হয়। ফলে বিকিরণের উজ্জ্বলতা বৃদ্ধি পায়।
৪। নিউটনীয় বলবিদ্যায় ফোটনের ভর ব্যাখ্যা করা যায় না। ফোটনের যে ভর আছে এই ধারণা বর্জনীয়। সহজে বলা যায়, ফোটনের স্থির ভর শূন্য ।
৫। আপেক্ষিকতা তত্ত্ব অনুসারে কোনো কণার স্থির ভর m এবং ভরবেগ p হলে,
কণাটির শক্তি, E = √(p2c2 +mo2c4)
ফোটনের ক্ষেত্রে, mo = 0
সুতরাং, E = pc
বা. p = E/c
বা, P = hf/c ………………..(5)
অর্থাৎ, ফোটন ভরহীন কণা হলেও এর সুনির্দিষ্ট ভরবেগ আছে।
উদাহরণ ১:
একটি মাইক্রোওভেন থেকে 0.01m তরঙ্গদৈর্ঘ্যের তাড়িতচৌম্বক তরঙ্গ নির্গত করছে। মাইক্রোওভেন থেকে নির্গত ফোটনের শক্তি নির্ণয় করন।
সমাধানঃ
দেয়া আছে, 1 = 0.01m, E = ?
আমরা জানি, E = hf
বা, E=h(c/λ)
মান বসালে, E = 6.63×10-34 (3×108 /0.01) = 1.99×10-23 J
উ: 1.99 ×10-23 J
উদাহরণ ২:
একটি 100 MeV ফোটনের কম্পাঙ্ক ও তরঙ্গদৈর্ঘ্য নির্ণয় করন।
সমাধানঃ
দেয়া আছে, E = 100 MeV = 100×10 x 1.6×10-19J=1.6×10-11J,
c=3×108ms-1, h= 6.63×10-34Js, f = ? এবং λ =?
আমরা জানি, E = hf
বা, f = E/h
মান বসালে, f = E/h = (1.6×10-11)/ (6.63×10-34) = 2.41×1022Hz. উত্তর
আবার, E = hf = h(c/λ) বা, λ = h(c/E)
মান বসালে, λ= 6.63×10- 34 x (3×108/ 1.6×10-11) = 1.24×10-14m উত্তর।
অথবা, c = vλ বা, λ = c/f = 3×108/2.41×1022 -= 1.24×10-14m
উ: 1.24×10-14m
সার-সংক্ষেপ :
কৃষ্ণ বস্তু:
যে বস্তু এর উপর আপতিত সকল তরঙ্গ দৈর্ঘ্যের বিদ্যুৎ-চৌম্বকীয় বিকিরণ শোষন করে অর্থাৎ কোন প্রতিসরণ বা প্রতিফলন হয় না তাকে কৃষ্ণ বস্তু বলে। কৃষ্ণ বস্তু থেকে সকল কম্পাংকের বিকিরণ সুষম ভাবে নিঃসরণ করে। কৃষ্ণ বস্তু যে বিকিরণ নিসঃরণ করে তাকে কৃষ্ণ বস্তুর বিকিরণ বলে। কৃষ্ণ বস্তু একটি আদর্শ বিকিরক।
ম্যাক্স পণ্ঢণ্ঢ্যাংকের কোয়ান্টাম তত্ত্ব:
তাড়িতচৌম্বক তরঙ্গ কোনো অবিচ্ছিন্ন তরঙ্গ নয় বরং বিচ্ছিন্ন তরঙ্গ এবং প্রতিটি কোয়ান্টা এক একটি অবিভাজ্য একক। প্রতিটি কোয়ান্টা আকার তার বা শক্তি তাড়িতচৌম্বক তরঙ্গের কম্পাংকের উপর নির্ভশীল। পরে ১৯২৬ সালে লুইস | প্রতিটি কোয়ান্টার নাম দেন ফোটন। সুতরাং প্রতিটি ফোটনের শক্তি হলো hf । কোয়ান্টাম তত্ত্বের মূল কথা হলো, | তাড়িতচৌম্বক বিকিরণ তরঙ্গধর্মী নয়, বরং এক ধরণের কণার স্রোত, এই কণার নাম ফোটন (Photon)।
বহুনির্বাচনী প্রশ্নঃ
১. কৃষ্ণ বস্তুর
i. উপর আপতিত সকল তরঙ্গ দৈর্ঘ্যের তাড়িত চৌম্বক বিকিরণ শোষন করে ।
ii. থেকে সকল কম্পাংকের বিকিরণ সুষম ভাবে নিঃসৃত হয়।
iii. উদাহরণ হিসাবে সূর্য্য একটি আদর্শ কৃষ্ণ বস্তু । নিচের কোনটি সঠিক?
ক. i ও ii
খ. i ও iii
গ. ii ও iii
ঘ. i, ii ও iii
২. নীচের কোনটি উইনের সমীকরণ?
ক. λmT = k
খ. E = ∂T4
st. E = hf
ঘ. p = hf/c
