আধুনিক পদার্থবিজ্ঞানের গুরুত্বপূর্ণ বিষয়

আজকে আমরা আধুনিক পদার্থবিজ্ঞানের গুরুত্বপূর্ণ বিষয় আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৮ এর  আধুনিক পদার্থবিজ্ঞান এর অন্তর্ভুক্ত।

আধুনিক পদার্থবিজ্ঞানের গুরুত্বপূর্ণ বিষয়

আলোর দ্বৈত প্রকৃতি (Dual Nature of Light)

আমরা জানি আলোর উপরিপাতনের ফলে ব্যাতিচার (interference), অপবর্তন (difference) ঘটে। আলায় আলোয় মিথস্ক্রিয়ার (interaction) ফলে এইরূপ হয়। ব্যতিচার, অপবর্তন এবং অন্যান্য আলোকীয় ঘটনা যেমন, প্রতিফলন (reflaction), প্রতিসরণ (refraction), পোলারায়ণ (polarization) এর পরীক্ষামূলক ফলাফল থেকে এই সিদ্ধাড়ে উপনীত হওয়া যায় যে, আলো তরঙ্গাকারে গতিশীল সুতরাং এই ঘটনাগুলো তরঙ্গ তত্ত্ব এবং বিকিরণের তাড়িতচৌম্বক তত্ত্ব দিয়ে সম্পূর্ণরূপে ব্যাখ্যা করা যায় ।

অপরদিকে অন্য জাতীয় ঘটনা যা বিকিরণ এবং কণার মিথষ্ক্রিয়ার ফলে ঘটে যেমন কৃষ্ণবস্তুর বিকিরণ, আলো তড়িৎ ক্রিয়া, কম্পটন ক্রিয়াগুলোকে তরঙ্গ তত্ত্ব এবং বিকিরণের তাড়িতচৌম্বক তত্ত্ব দিয়ে ব্যাখ্যা করা যায় না। আমার দেখেছি এগুলো ব্যাখ্যা করার জন্য বিকিরণ শক্তিকে ক্ষুদ্র ক্ষুদ্র শক্তির প্যাকেটের গুচ্ছ প্রবাহ আকারে বিবেচনা করা হয়। এই শক্তিকে আলোর কোয়ান্টা (quanta) বা ফোটন (photon) বলে। প্রতিটি ফোটনের শক্তি মান E = hf । যেখানে কম্পাংক f = c/λ এখানে λ হলো বিকিরণের তরঙ্গ দৈর্ঘ্য। বিকিরণ শক্তি যখন কণার সাথে মিথষ্ক্রিয়া ঘটায় তখন ফোটন তার সমস্ড় শক্তি কণাকে দান করে।

আলোর কণা ধর্ম এবং তরঙ্গ ধর্ম অর্থাৎ দ্বৈত ধর্ম আছে। হাইজেনবার্গ প্রস্তাব করেন যে আলোর দ্বৈত ধর্ম বিদ্যমান তবে এরা পরস্পরের পরিপূরক। অর্থাৎ একই পরীক্ষায় আলো কখনই তার দ্বৈত ধর্ম প্রকাশ করে না। অর্থাৎ কোন পরীক্ষায় যদি আলো তার তরঙ্গ ধর্ম প্রদর্শন করে তবে সেই পরীক্ষা দ্বারা কোনো ভাবেই আলোর কণা ধৰ্ম পর্যবেক্ষণ করা সম্ভব নয়। অনুরূপ ভাবে বিপরীত ঘটনাও সত্য।

পরবর্তিতে ডি ব্রগলী (De-Broglie) বহু সংখ্যক তরঙ্গের উপরিপাতনের ফলে সৃষ্ট গুচ্ছ তরঙ্গের (gorup wave) ধারণা দেন এবং ভরবেগের সাথে তরঙ্গ দৈর্ঘ্যে একটি সম্পর্ক λ =  h/p স্থাপন করেন। তিনি আরো প্রস্তুাব করেন যে আলোর যেমন কণা ধর্ম বিদ্যমান তেমনি কণারও তরঙ্গ ধর্ম বিদ্যমান। ১৯২৪ সালে ডি ব্রগলী প্রস্তুাব করেন যে, আলোর ন্যায় পরমাণবিক ডুরের কণাও (যেমন ইলেকট্রন) আলোর ন্যায় দ্বৈত ধর্ম প্রদর্শন করে এবং ১৯২৭ সালে পরীক্ষার মাধ্যমে তা প্রমাণ করেন ।

পদার্থ তরঙ্গ (Matter Wave):

তরঙ্গ যেমন কিছু ক্ষেত্রে কণার নায় আচরণ করলেও কণা যে কিছু ক্ষেত্রে তরঙ্গের ন্যায় আচরণ করে সে বিষয় ১৯২৪ খ্রিস্টাব্দে ফরাসি বিজ্ঞানী ডি ব্রগলী (De-Broglie) প্রথম উপস্থাপন করেন। তার এই সিদ্ধান্দ্রের পিছনে নীচের কারণগুলো যুক্তি সংগত।

১। প্রকৃতি প্রতিসাম্য (Symmetry) পছন্দ করে। প্রকৃতির দুটি সত্তা-পদার্থ ও শক্তি অবশ্যই প্রতিসাম্য থাকবে।

২। শক্তি (বিকিরণ) যদি তরঙ্গরূপী ও কণারূপী হয় তবে পদার্থও তরঙ্গরূপী ও কণারূপী হবে।

৩। একটি আলোকরশ্মিগুচ্ছ (যা একটি তরঙ্গ) কোনো বস্তুর বিভিন্ন বিন্দুতে শক্তি ও ভরবেগ হান্ড্ররিত করতে পারে, আবার একটি কণার স্রোতও কোনো বস্তুর বিভিন্ন বিন্দুতে শক্তি ও ভরবেগ হড়ম্প্ররিত করতে পারে। সুতরাং কণার স্রোত পদার্থ তরঙ্গ হবে ।

ডি ব্রগলীর সমীকরণ (De Broglie Equation)

ডি-ব্রগলী কণা ধর্ম এবং তরঙ্গ ধর্মকে সম্পর্কযুক্ত করে যে সমীকরণ প্রতিপাদন করেন তা ডি ব্রগলী সমীকরণ নামে পরিচিত ।
ডি-ব্রগলী তার সমীকরণটি কেবল মাত্র প্রতিষ্ঠিত দুইটি সমীকরণকে সংযোগের মাধ্যমে প্রতিপাদন করেন,
পশ্চাঙ্কের কোয়ান্টাম তত্ত্ব অনুসারে একটি ফোটনের শক্তি,
E = hf .………………..(1)

আইনস্টাইনের আপেক্ষিকতার সূত্র অনুসারে, E2 = p2c2 + mo2c4 .………………..(2)

ফোটনের ক্ষেত্রে এর স্থির ভর mo = 0

সুতরাং ফোটনের ক্ষেত্রে আইনস্টাইনের সূত্র থেকে E2 = p2c2 + 0

বা, E = pc

বা, P = E/c = hf/c = h/(c/f) = h/λ

[পণ্ডাঙ্কের সূত্র ব্যবহার করে]        [: c = fλ]

বা, λ = h /P .………………..(3)

এটাই ডি ব্রগলীর সমীকরণ নামে পরিচিত।

এই সমীকরণে তেজশক্তির দ্বৈত প্রকৃতি প্রকাশিত হয়েছে। অর্থাৎ কণা ধর্ম ভরবেগর সাথে তরঙ্গ ধর্ম তরঙ্গ দৈর্ঘ্যের সম্পর্ক স্থাপিত হয়েছে। এই সমীকরণ দ্বারা ফোটনের কণা ধর্ম প্রদর্শীত হয়েছে। ডি-ব্রগলীর আরো উলেণ্ঢখ করেন যে, ফোটনের মত প্রতিটি কণারই তরঙ্গ ধর্ম বিদ্যমান। সেক্ষেত্রে, p = mv, এখানে m হলো কণার ভর । অতএব, কণার অনুসঙ্গী ডি-ব্রগলীর তরঙ্গ দৈর্ঘ্য,

λ = h /mv .………………..(4)

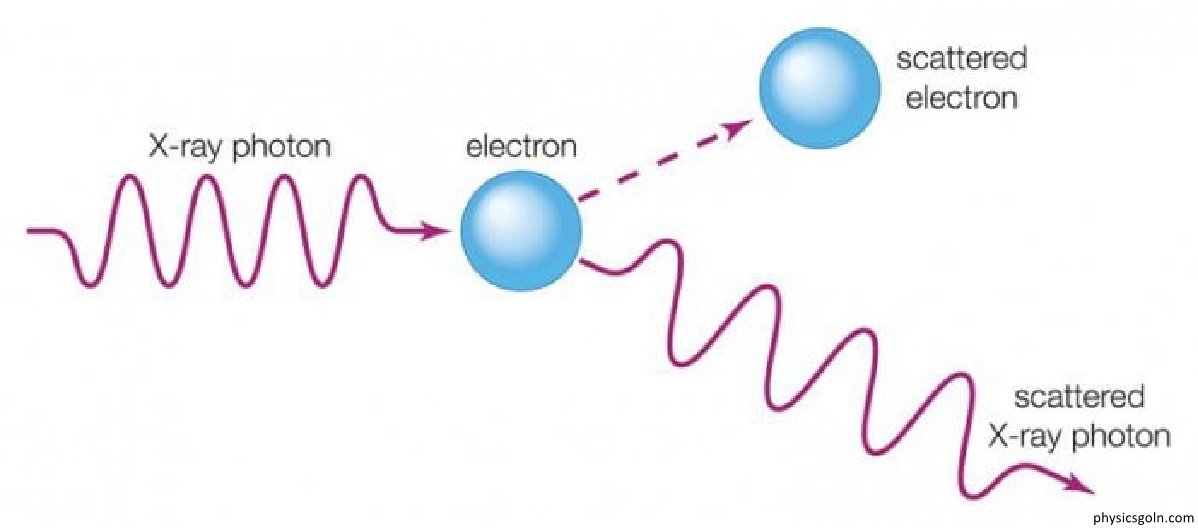
ডি-ব্রগলীর প্রকল্পের সম্পূর্ণ বিবৃতিঃ

যে কোনো কণার স্রোত তরঙ্গের ন্যায় আচরণ করে। যা পদার্থ তরঙ্গ নামে পরিচিত

এই পদার্থ তরঙ্গের তরঙ্গদৈর্ঘ্য, λ = h /P = h /mv

এখানে, m= কণার ভর, v = কণার বেগ এবং p = কণার ভরবেগ ।

তরঙ্গদৈর্ঘ্য (তরঙ্গের একটি বৈশিষ্ট্য) ও ভরবেগ (কণার একটি বৈশিষ্ট্য) নিয়ে সম্পর্কিত λ = h /mv সমীকরণ থেকে নীচের
সিদ্ধাড়গুলিতে আসা যায় ।

১। যদি v = 0 হয় তবে λ = ∞ হবে অর্থাৎ কেবল মাত্র গতিশীল কণার সাথেই পদার্থ তরঙ্গ জড়িত থাকে।

২। কণাটি চার্জিত না অচার্জিত তার উপর ডি ব্রগলী তরঙ্গদৈর্ঘ্য নির্ভরশীল নয়। এর অর্থ হলো পদার্থ তরঙ্গ তাড়িতচৌম্বক তরঙ্গ নয়। কারণ তাড়িতচৌম্বক তরঙ্গ ত্বরণসম্পন্ন চার্জ থেক উৎপন্ন হয় ।

৩। কণার ভর (m) অথবা বেগ (v) এর মান বড় হলে ডি ব্রগলী তরঙ্গদৈর্ঘ্য (2) খুব ছোট হয়।

৪ । কণার ভরবেগ (p) বৃদ্ধি পেলে ডি ব্রগলী তরঙ্গদৈর্ঘ্য (2) হ্রাস পায়।

৫। যেহেতু পদার্থ তরঙ্গ পদার্থের সংশিষ্ট তরঙ্গ সেহেতু কণার বেগ এবং পদার্থ তরঙ্গের বেগ সমান। অর্থাৎ কণা যেখানে অবস্থান করে পদার্থ তরঙ্গও সেখানে অবস্থান করে ।

৬। যেহেতু যে কোনো কণার স্রোতকে পদার্থ তরঙ্গ হিসাবে ধরে নেয়া চলে সেহেতু কণার স্রোত যদি বাঁধাহীনভাবে অগ্রসর হতে থাকে তবে সংশিষ্ট পদার্থ তরঙ্গটি চল তরঙ্গ হিসাবে আচরণ করবে।

৭। অপরদিকে কণার স্রোত যদি একটি নির্দিষ্ট অঞ্চলে সীমাবদ্ধ থাকে তবে পদার্থ তরঙ্গ স্থির তরঙ্গের ন্যায় আচরণ করবে।

কম্পটন ক্রিয়া (The Compton Effect)

একটি একবর্ণী X -রশ্মি অ্যালুমনিয়াম, গ্রাফাইট (কার্বন) প্রভৃতি হালকা মৌলের ইলেকট্রন দ্বারা বিক্ষিপ্ত (scattered) হলে
বিক্ষিপ্ত রশ্মির মধ্যে অপরিবর্তিত তরঙ্গ দৈর্ঘ্য ছাড়াও পরিবর্তিত তরঙ্গদৈর্ঘ্যে X-রশ্মি পাওয়া যায়। এই পরিবর্তিত তরঙ্গদৈর্ঘ্যগুলি প্রাথমিক X-রশ্মির তরঙ্গদৈর্ঘ্যের চেয়ে দীর্ঘতর। বিজ্ঞানী আর্থার কম্পটন এই ঘটনা আবিষ্কার করেন। তাঁর নাম অনুসারে এই ঘটনাকে কম্পটন ক্রিয়া বলে।

চিরায়ত তাড়িতচৌম্বক তরঙ্গতত্ত্ব এই ঘটনাকে সম্মেষজনক যা E = hf ব্যাখ্যা দানে অসমর্থ। এই তত্ত্বানুসারে X -রশ্মি একটি অতিক্ষুদ্র তরঙ্গদৈর্ঘ্যর তাড়িতচৌম্বক তরঙ্গ হিসাবে ইলেকট্রনের উপরে একটি পরিবর্তিত (সাইন আকৃতির) তাড়িতচৌম্বক ক্ষেত্র প্রয়োগ করবে ফলে ইলেকট্রনটি একই কম্পাঙ্গে কম্পিত হতে থাকবে।

চিরায়ত তত্ত্বানুসারে কম্পমান চার্জ একই কম্পাঙ্কের তাড়িতচৌম্বক বিকিরণ প্রদানে সক্ষম। ভিন্ন কম্পাঙ্গে অর্থাৎ ভিন্ন তরঙ্গদৈর্ঘ্যের উপস্থিতি সম্পর্কে এই তত্ত্ব ব্যাখ্যা প্রদানে অক্ষম।

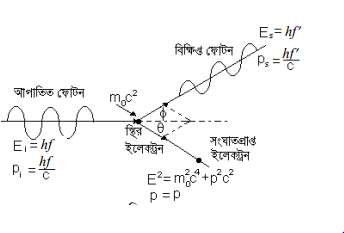
আইনস্টাইনের ফোটন তত্ত্বের ভিত্তিতে কম্পটন তার কম্পটন তত্ত্বের ব্যাখ্যা দেন। ফোটন ভরবিহীন কণার ন্যায় আচরণ
hf করে। এর প্রতিটি কণার শক্তি E = hf । এখানে, h হলো পণ্ঢাংকের ধ্রুবক। এর ভরবেগ Pi = hf/c। একটি ফোটন ও একটি ইলেকট্রনের মধ্যে সংঘর্ষকে চিরায়ত বলবিদ্যার বিলিয়ার্ড বলের সংঘর্ষের ন্যায় সংঘর্ষ হিসাবে বিবেচনা করা,যেতে পারে ।

মনে করি পরীক্ষাগার স্থানাঙ্ক কাঠামোতে একটি mo স্থির ভর বিশিষ্ট ইলেকট্রনের সাথে একটি X-রশ্মি-ফোটনের সংঘর্ষ হলো ফলে ফোটন কিছু পরিমান শক্তি হারিয়ে Es = hf’ এবং ভরবেগ Ps = hf’/c  হলো। এখানে f’ হলো পরিবর্তিত কম্পাঙ্ক। আর ইলেকট্রন সেই শক্তি গ্রহণ করে গতিশক্তি প্রাপ্ত হলো। সংঘর্ষের পর বিক্ষিপ্ত ফোটন ও প্রতিক্ষিপ্ত (recoil) ইলেকট্রন আপতিত ফোটনের দিকের সাথে যথাক্রমে ∅ ও 8 কোণ উৎপন্ন করে ।

তাহলে, ফোটনের শক্তি ক্ষয় = ইলেকট্রনের গতিশক্তি অর্জন, T = hf – hf’

বা, T = h(f – f’) .………………..(5)

mo স্থির ভর বিশিষ্ট ইলেকট্রনের শক্তি moc2 এবং ভরবেগ শূন্য।

সংঘাতের পর ইলেকট্রনের মোটশক্তি, E = T + moc2

(5) নং সমীকরণের মান বসালে, E = h(f – f’)+ mgc2

বা, E2 = [h(f – f’)+ moc2]2

বা, E2 = h2 (f – f’) + mo2c4+ 2h (f – f’)moc2

বা, E2 = h2 (f2 + f’2 – 2ff’) + mo2c4+ 2h (f – f’)moc2 .………………..(6)

আপেক্ষিক তত্ত্বানুসারে সংঘাতের পর ইলেকট্রনের মোটশক্তি,

E² = p²c² + mo²c4 .………………..(7)

(7) নং সমীকরণের মান (6) নং সমীকরণে বসালে,

:. p²c² + mo² c4 = h² (ƒ² + ƒ’² − 2 ff’) + m² c4 +2h(ƒ − ƒ’)moc²

বা, p²c²=h² (ƒ² + ƒ¹² – 2ƒƒ’)+2h(ƒ -ƒ’)moc² .………………..(8)

আবার ভবেগের নিত্যতার সূত্রানুসারে x-অক্ষ বরাবর ভরবেগ, hf hf’ +0= с с -cos+pcos

বা, hf = hf’cosφ + pc cos8

বা, pccos8 = hf-hf’cosφ

বা, (pccos8)2 = (hf – hf’cosφ)2

বা, p²c² cos²8 = h²ƒ² – 2h² ff’ cosφ + h²ƒ’² cos²φ …………………(9)

আবার, ভরবেগের নিত্যতার সূত্রানুসারে Y-অক্ষ বরাবর ভরবেগ, 0 = (hf’/c)sinφ – psin8

বা,0=hf’sinφ – pc sin8

বা,p2c2 sin28 = h²ƒ’² sin²φ …………………(10)

(9) ও (10) নং সমীকরণকে যোগ করলে,

p2c² sin20+ p²c² cos² 0 = h2f2 – 2h2ff’cosφ +h² f’² cos²φ + h²ƒ’² sin²φ

বা, p²c²(sin²8+ cos²8) = h²ƒ² −2h² ff’cosφ + h²ƒ’² (cos²φ + sin²φ )

বা, p²c² = h²f2 – 2h² ff’cosφ +h² f’2

বা,p²c² = h² (ƒ² + ƒ’2 – 2 ff’cosφ) …………………(11)

(11) নং সমীকরণের মান (9) নং সমীকরণে বসালে,

h² (ƒ² + ƒ’² − 2 ff’cosφ)= h² (ƒ² + ƒ’² − 2ƒƒ’)+2h(ƒ – ƒ’)moc²

বা, -2h2 ff’cosφ =-2h² ff’ +2h(ƒ -ƒ’)moc²

বা, 2h(f-ƒ’)moc² = 2h² ff’ – 2h² ff’cosφ = 2h² ff'(1-cosφ)

বা, (f-ƒ’)/ ff’ = h/moc2′(1-cosφ)

বা, 1/f’ – 1/f =  h/moc2 (1-cosφ) …………………(12)

বা, c/f’ – c/f =  h/moc (1-cosφ) [: c = ƒλ]

বা,  λ’ – λ = ∆λ = h/moc (1-cosφ)

বা, ∆λ = h/mocsin²φ/ 2 ………………..(13)

(11), (12) ও (13) নং সমীকরণই কম্পটন ফলাফল সমীকরণ। এখানে ∆λ হলো তরঙ্গদৈর্ঘ্যের পরিবর্তন।

(11), (12) ও (13) নং সমীকরণটি নির্দেশ করে যে λ’ > λ বা f’ < f অর্থাৎ বিক্ষিপ্ত বিকিরণের তরঙ্গদৈর্ঘ্য আপতিত তরঙ্গদৈর্ঘ্য অপেক্ষা বৃহত্তর।

সমীকরণটি আরো নির্দেশ করে যে, তরঙ্গদৈর্ঘ্যে পরিবর্তন আপতিত ফোটনের কম্পাঙ্কের উপর বা বিক্ষেপ প্রকৃতির উপর নির্ভরশীল নয় শুধু মাত্র বিক্ষেপ কোণের উপর নির্ভরশীল।

যদি বিক্ষেপ কোণ φ = π/2 হয় তবে cosφ =0, তখন (12) নং সমীকরণ থেকে ∆λ = λ’ – λ = h /moc

এই ধ্রুবক h /moc কে বিক্ষেপ কণার কম্পটন তরঙ্গদৈর্ঘ্য বলে এবং λk দ্বারা প্রকাশ করা হয়।

অতএব, ইলেকট্রনের কম্পটন তরঙ্গদৈর্ঘ্য,

λk =  h /moc = (6.625×10-34)/(9.1×10-3¹×3×108) = 0.0242 A ………………..(14)

এখানে আরো লক্ষণীয় যে, কম্পটন তরঙ্গদৈর্ঘ্য λk = h/moc থেকে লেখা যায়, moc = h/ λk

বা, moc²  = hc/λk = hfk

এখানে, moc2 হলো ইলেকট্রনের স্থির ভর-শক্তি। সুতরাং, বলা যায় কম্পটন তরঙ্গদৈর্ঘ্য প্রকৃত পক্ষে বিক্ষিপ্ত ইলেকট্রনের স্থির ভর-শক্তির তরঙ্গদৈর্ঘ্যের সমান ।

যদি বিক্ষেপ কোণ φ = π হয় তবে cosφ = -1,

তখন (12) নং সমীকরণ থেকে, ∆λ = λ’ – λ = 2h/moc

সুতরাং, কম্পটন ক্রিয়ায় X-রশ্মি-ফোটনের সর্বোচ্চ তরঙ্গদৈর্ঘ্যের পরিবর্তন

2h/moc = 2 × 0.0242Å = 0.0484Å

কম্পটন তত্ত্বের সীমাবদ্ধতা

১। কম্পটন তত্ত্বে বিক্ষিপ্ত তরঙ্গে কেন আপতিত তরঙ্গ উপস্থিত থাকে তার ব্যাখ্যা নাই । নিম্নে আপতিত তরঙ্গে উপস্থিতির ব্যাখ্যা দেয়া হলো। কম্পটন তত্ত্বে ফোটনের পরমাণুর সাথে বহিঃকক্ষপথে হালকা ভাবে আবদ্ধ ইলেকট্রনের সংঘর্ষ ঘটে। তাছাড়াও ফোটন দৃঢ়ভাবে আবদ্ধ অভ্যীণ ইলেকট্রনের সাথে সংঘর্ষ ঘটায়। সে সব ইলেকট্রন পরমাণু থেকে বিচ্ছিন্ন হতে পারেনা।

ফলে সমগ্র পরমাণু প্রতিক্ষিপ্ত (recoil) হয়। এই ধরণের সংঘর্ষে ইলেকট্রনের ভর এর পরিবর্তে পরমাণুর সমগ্র ভর কার্যকর হয়। যেহেতু পরমাণুর ভর ইলেকট্রনের স্থির ভরের চেয়ে কয়েক হাজারগুণ বেশী তাই তরঙ্গদৈর্ঘ্যের কোন পরিবর্তন হয়না।

উদাহরণ স্বরূপ গ্রাফাইট পরমাণুর ভর, Mc =12×1840 mo, এখানে mo ইলেকট্রনের স্থির ভর।

আমরা জানি কম্পটন তরঙ্গদৈর্ঘ্যের পরিবর্তন ∆λ = (2h/moc)sinφ/2

ইলেকট্রনের স্থির ভর mo এর স্থলে সমগ্র পরমাণুর ভর Mc বসালে, ∆λ = (2h/Mcc)sin2φ/2

∆λ এর মান সর্বোচ্চ হয় যখন ফোটনের বিক্ষেপ কোণ সর্বাধিক অর্থাৎ, φ = π হবে। 2 22

বা, ∆λ = (2h/Mcc)sin2φ/2 = 1/(12×1840)(2h/Mcc)sin2π/2

বা, ∆λ = 9.058×10-5 x 0.02426 Å

বা, ∆λ = 2.197×10-8Å

অর্থাৎ, ∆λ এর মান অত্যন্ত্ কম। সুতরাং ফোটন দৃঢ়ভাবে আবদ্ধ অভ্যীণ ইলেকট্রনের সাথে সংঘর্ষ ঘটলে তরঙ্গদৈর্ঘ্য অপরিবর্তিত থাকে ।

২। পরীক্ষায় দেখা যায় যে, হালকা পরমাণু দ্বারা বিক্ষিপ্ত X-রশ্মি-ফোটনের পরিবর্তিত তরঙ্গ আপতিত তরঙ্গ অপেক্ষা প্রাবল্য বেশী কিন্তু ভারী পরমাণু দ্বারা বিক্ষিপ্ত X-রশ্মি-ফোটনের পরিবর্তিত তরঙ্গ আপতিত তরঙ্গ অপেক্ষা প্রাবল্য কম। এই পরীক্ষালব্ধ ফলাফল কম্পটন তত্ত্ব দ্বারা ব্যখ্যা করা যায় না।

 হাইজেনবার্গে-এর অনিশ্চয়তা নীতি (Heisenberg Uncertainty Principle)

হাইজেনবার্গের অনিশ্চয়তা নীতি অনুসারে আণবিক স্ত্বরে কোনো গতিশীল কণার ক্ষেত্রে নির্দিষ্ট দিকে এর অবস্থান ও ভরবেগ যুগপৎ সঠিক ভাবে পরিমাপ করা সম্ভব নয়। হাইজেনবার্গের অনিশ্চয়তা নীতি নিম্নে দেয়া হলো,

আনবিক ডুরে হার্মিশিয়ান আইনানুগ জোড় (যেমন অবস্থান-ভরবেগ, সময়-শক্তি, কৌণিক অবস্থান-কৌণিক ভরবেগ ইত্যাদি) যুগপৎ সঠিক ভাবে পরিমাপ করা সম্ভব নয়। হার্মিশিয়ান আইনানুগ জোড়গুলোর অনিশ্চয়তার ত্র“টির গুণফল পণ্ঢাংকের হ্রাসকৃত ধ্রুব । অপেক্ষা বৃহত্তর বা সমান ।

যেমন, নির্দিষ্ট দিকে কোনো কণার অবস্থান ও ভরবেগ যুগপৎ সঠিক ভাবে পরিমাপ করা সম্ভব নয়। আনবিক জ্বরে X- অক্ষ বরাবর গতিশীল কোনো কণার কোন এক সময় অবস্থানের অনিশ্চয়তা বা অবস্থান জনিত ত্র“টি Ax এবং ঐ সময় ভরবেগ অনিশ্চয়তা বা ভরবেগ জনিত ত্র“টি Ap এর গুণফল পণ্ঢ্যাংকের হ্রাসকৃত ধ্রুবক h অপেক্ষা বৃহত্তর বা সমান ।

অর্থাৎ,  ∆x∆p≥ h [ যেখানে h = h/2π ………………..(15)

অনুরূপভাবে Y ও Z- অক্ষ বরাবর যথাক্রমে,

∆y∆p ≥ h

এবং ∆z∆p≥ h

অনিশ্চয়তা নীতির আর এক রূপ এর ক্ষেত্র হলো কণার শক্তি E এবং যখন এই শক্তি পরিমাপ করা হচ্ছে তখন সময় t ।

এই চলকের ক্ষেত্রে অনিশ্চয়তার নীতি হলো ∆E∆t ≥ h যখন ∆E হলো শক্তি অনিশ্চয়তা এবং ∆t হলো সময়ের অনিশ্চয়তা।

উপরিউক্ত সূত্রগুলো সাহায্যে আমরা বুঝতে পারি যে, যন্ত্র যত সূক্ষ্ণই হোক না কেন আণবিক পালণ্ঢায় পরিমাপের ক্ষেত্রে
নির্দিষ্ট ভুলের সীমার অতিক্রম করা কখনই সম্ভব নয়। কোনো বস্তুর অবস্থান যদি আমরা সঠিক ভাবে পরিমাপ করতে সক্ষম
হই তবে ভরবেগের ত্র“টি হবে সর্বাধিক এবং এর বিপরীত ক্রমের ক্ষেত্রও সত্য। সুতরাং একই সঙ্গে অবস্থান ও ভরবেগ যুগপৎ সঠিক ভাবে নির্ণয় করা সম্ভব নয়। অনুরূপ ভাবে শক্তি ও সময় যুগপৎ সঠিক ভাবে নির্ণয় করা সম্ভব নয়। এই তত্ত্বটি মূলতঃ কণার দ্বৈত প্রকৃতি নির্দেশ করে। কণার যদি দ্বৈত প্রকৃতি না থাকতো তবে পরিমাপের ক্ষেত্রে এই অনিশ্চয়তার উদ্ভব হতো না ।

অনিশ্চয়তা নীতির ভৌত তাৎপর্য

অনিশ্চয়তা নীতি ∆x∆px≥ h থেকে নি— লিখিত সিদ্ধাড়ে উপনিত হওয়া যায়,

১) যদি কোন উন্নত পরীক্ষা দ্বারা কণার অবস্থান কোন এক মূহুর্তে সঠিক ভাবে পরিমাপ করা যায় অর্থাৎ অবস্থান জনিত অনিশ্চয়তা ∆x = 0 হয় তবে সেই মুহুর্তে ভরবেগ জনিত অনিশ্চয়তা ∆p অসীম হয়ে যাবে।

২) যদি কোন উন্নত পরীক্ষা দ্বারা কণার ভবেগে কোন এক মূহুর্তে সঠিক ভাবে পরিমাপ করা যায় অর্থাৎ ভরবেগ জনিত অনিশ্চয়তা Ap,= 0 হয় তবে সেই মুহুর্তে অবস্থান জনিত অনিশ্চয়তা ∆x অসীম হয়ে যাবে। সুতরাং একই সঙ্গে অবস্থান ও ভরবেগ যুগপৎ সঠিক ভাবে নির্ণয় করা সম্ভব নয়। সঠিকতার সীমা হাইজেনবার্গের অনিশ্চয়তা নীতি দ্বারা নির্ধারণ করা যায়।

৩) m ভরের কণা X অক্ষ বরাবর v বেগে গতিশীল হলে তার অবস্থানের অনিশ্চয়তা ∆x এবং ঐ সময় বেগের অনিশ্চয়তা ∆v এর গুণফল অনিশ্চয়তা নীতি অনুসারে ∆x.∆v≥ h/2 [যেহেতু p = mv] m

ভারী কণার ক্ষেত্রে h/m খুবই ক্ষুদ্র। সেক্ষেত্রে ∆x এবং ∆v এর গুণফলও খুব ক্ষুদ্র হয়ে আসে। তাই এমতাবস্থায় কণা
অবস্থান ও v বেগে সঠিকভাবে নিরূপণ করা যায়। খুব ভারী কণার ক্ষেত্রে h/m = 0 ফলে অনিশ্চয়তা নীতি আর থাকে m না। এটাই হলো চিরায়ত বলাবদ্যার সীমানা। সুতরাং ভারী বস্তুর ক্ষেত্রে চিরায়ত বলবিদ্যা সত্য এবং হালকা বস্তুর (যেমন ইলেকট্রন, প্রোটন, নিউট্রন ইত্যাদি) ক্ষেত্রে কোয়ান্টাম বলবিদ্যা কার্যকর।

অনিশ্চয়তা নীতি প্রয়োগ:

অনিশ্চয়তা নীতি প্রয়োগ করে নিউক্লিয়াসের মধ্যে মুক্ত ইলেকট্রন থাকতে পারে না । আমরা জানি,

১। তেজস্ক্রিয় নিউক্লিয়াস থেকে B-রশ্মি নির্গত ইলেকট্রনের সর্বোচ্চ গতিশক্তি প্রায় 4 Mev

২। ইলেকট্রনের স্থির ভর mo = 9.11×103 kg

৩। নিউক্লিয়াসের ব্যাস d = 2 x 10-14 m

যদি নিউক্লিয়াসের মধ্যে মুক্ত ইলেকট্রন বিদ্যমান থাকে তবে নিউক্লিয়াসের এই ব্যাসের গোলকের মধ্যে কোথাও না কোথাও
অবস্থিত হবে। সুতরাং নিউক্লিয়াসে ইলেকট্রনে অবস্থান জনিত সর্বোচ্চ অনিশ্চয়তা,

∆x=2×10-14m = নিউক্লিয়াসের ব্যাস।

ইলেকট্রনের অবস্থান ও ভরবেগের অনিশ্চয়তার গুণফল, হাইজেনবার্গের অনিশ্চয়তার নীতি থেকে লিখতে পারি,

∆x∆p ≥ h  ∆p ≥h/∆x

যেহেতু, ∆x = ইলেকট্রনে অবস্থান জনিত সর্বোচ্চ অনিশ্চয়তা সেহেতু ∆P = ইলেকট্রনে ভরবেগ জনিত সর্বনিম্ন অনিশ্চয়তা।

সুতরাং নিউক্লিয়াসে অবস্থিত ইলেকট্রনের সর্বনি— ভরবেগ জনিত অনিশ্চয়তা,

∆P = h/2π∆x= (6.63×10-34)/(2π × 2 ×10-14) = 5.278×10-24 kgms-1

অর্থাং নিউক্লিয়াসে যদি মুক্ত ইলেকট্রন থাকতে হয় তবে তার সর্বনি— ভরবেগ হবে, Pmin = 5.278×10 2 kgms-1

অতএব, Emin =  P2min/ 2m = (5.278×10-21) /(2×9.1×10-31) J

= 1.53062×10-11J =(1.53062×10-11 /1.6×10-19)eV

= 0.9566375×108eV = 95.66MeV

অতএব নিউক্লিয়াসে মুক্ত ইলেকট্রন থাকতে হলে তার সর্বনিম্ন শক্তি 96Mev ক্ষেত্রে এর কাছাকাছি হতে হবে। কিন্তু তেজস্ক্রিয়
নিউক্লিয়াস থেকে B-রশ্মির সর্বোচ্চ গতিশক্তি প্রায় 4Mev | সুতরাং নিউক্লিয়াসে মুক্ত ইলেকট্রন থাকতে পারে না ।

উদাহরণ ১:

একটি ফোটনের তরঙ্গ দৈর্ঘ্য 4×10-7m । এর রৈখিক ভরবেগ কত?

সমাধান:

দেয়া আছে,

λ = 4×10-7m, h = 6.63×10-34Js এবং p = ?

আমরা জানি,

ফোটনের ভরবেগ, p = h/λ

মান বসালে, P = 6.63×10-34/ 4×10-7

=1.66×10-27kgms-1

উ : 1.66×10-27 kgms-1

উদাহরণ ২ :

একটি ইলেকট্রনের কম্পটন তরঙ্গদৈর্ঘ্য বের কর না।

সমাধানঃ

দেয়া আছে, h = 6.63×10-34Js, m = 9.1×10 kg, c = 3×10 ms-1 এবং ∆λ = ?

আমরা জানি,

কম্পটন তরঙ্গদৈর্ঘ্য, ∆λ = h/mec

মান বসালে, ∆λ = h/ mec

= (6.63×10-34/ 9.1×10-3×3×108)

= 0.0248 A

উ : 0.0248 4

সার-সংক্ষেপ :

আলোর প্রকৃতি :

আলোর কণা ধর্ম এবং তরঙ্গ ধর্ম অর্থাৎ দ্বৈত ধর্ম আছে। হাইজেনবার্গ প্রস্তাব করেন যে আলোর দ্বৈত ধর্ম বিদ্যমান তবে এরা পরস্পরের পরিপূরক। অর্থাৎ একই পরীক্ষায় আলো কখনই তার দ্বৈত ধর্ম প্রকাশ করে না । পদার্থ তরঙ্গঃ তরঙ্গ যেমন কিছু ক্ষেত্রে কণার নায় আচরণ করে কণাও তেমনি কিছু ক্ষেত্রে তরঙ্গের ন্যায় আচরণ করে। কণার এই তরঙ্গকে পদার্থ তরঙ্গ বলে। এই তরঙ্গের সমীকরণ হলো, h mv = । এটাই ডি ব্রগলীর সমীকরণ নামে পরিচিত।

ডি-ব্রগলীর প্রকল্পের সম্পূর্ণ বিবৃতিঃ

যেকোনো কণার স্রোত তরঙ্গের ন্যায় আচরণ করে। যা পদার্থ তরঙ্গ নামে পরিচিত । এই পদার্থ তরঙ্গের তরঙ্গদৈর্ঘ্য, λ = h/p = h/
mv

কম্পটন ক্রিয়া:

একটি একবর্ণী X -রশ্মি অ্যালুমনিয়াম, গ্রাফাইট (কার্বন) প্রভৃতি হালকা মৌলের ইলেকট্রন দ্বারা বিক্ষিপ্ত | হলে বিক্ষিপ্ত রশ্মির মধ্যে অপরিবর্তিত তরঙ্গ দৈর্ঘ্য ছাড়াও পরিবর্তিত তরঙ্গদৈর্ঘ্যে X-রশ্মি পাওয়া যায়। এই পরিবর্তিত তরঙ্গদৈর্ঘ্যগুলি প্রাথমিক X-রশ্মির তরঙ্গদৈর্ঘ্যর চেয়ে দীর্ঘতর। বিজ্ঞানী আর্থার কম্পটন এই ঘটনা আবিষ্কার করেন। তাঁর নাম অনুসারে এই ঘটনাকে কম্পটন ক্রিয়া বলে।

হাইজেনবার্গে-এর অনিশ্চয়তা নীতি:

হাইজেনবার্গের অনিশ্চয়তা নীতি অনুসারে আনবিক ডুরে কোন গতিশীল কণার ক্ষেত্রে নির্দিষ্ট দিকে এর অবস্থান ও ভরবেগ যুগপৎ সঠিক ভাবে পরিমাপ করা সম্ভব নয়। অর্থাৎ, ∆x∆p ≥ h

বহুনির্বাচনী প্রশ্ন:

১. বিক্ষেপ কণার কম্পটন তরঙ্গদৈর্ঘ্য কোনটি?

ক. λ = h/p

খ. λ = h/mv

গ. ∆λ = (2h/moc)sinφ/2

ঘ. ∆λ = h/moc

২। নীচের কোনটি হাইজেনবার্গের অনিশ্চয়তা নীতি নয়?

ক. ∆x∆p ≥ h

খ. ∆E∆t ≥ h

গ. ∆8∆L ≥ h

ঘ. ∆p∆t ≥ h

৩। কণার অনুসঙ্গী ডি-ব্রগলীর তরঙ্গ দৈর্ঘ্য কোনটি?

ক. λ = h/p

খ. λ = h/mv

গ. P = E /C

ঘ. ∆λ = h/moc