কৌণিক ভরবেগ এবং জড়তার ভ্রামক জকের আলোচনার বিষয়। কৌণিক ভরবেগ এবং জড়তার ভ্রামক [Angular momentum and moment of inertia] ক্লাসটি পলিটেকনিক [Polytechnic] এর ফিজিক্স-১ (৬৫৯১২), Physics 1 এর, অধ্যায় ৩ এর টপিক। কৌণিক ভরবেগ কী এবং এর সাথে জড়তার ভ্রামকের কোন সম্পর্ক আছে কিনা তা এই ভিডিওতে নির্ধারণ করা হয়েছে ।
কৌণিক ভরবেগ এবং জড়তার ভ্রামক
কৌণিক ভরবেগ
পদার্থবিজ্ঞানে কৌণিক ভরবেগ, ভরবেগের ভ্রামক বা কৌণিক ভ্রামক দ্বারা এমন একটি ভেক্টর রাশিকে প্রকাশ করা হয়, যা কোনো অক্ষের সাপেক্ষে ঘূর্ণায়মান কোনো বস্তুর জড়তার ভ্রামক ও কৌণিক বেগের গুণফল থেকে পাওয়া যায়।
কোনো বস্তুর কৌণিক ভরবেগ হলো ঐ বস্তু গঠনকারী প্রত্যেকটি কণার কৌণিক ভরবেগের সমষ্টির সমান। কোনো অক্ষের সাপেক্ষে ঘূর্ণায়মান কোনো দৃঢ় বস্তুর কৌণিক ভরবেগ, (), এর জড়তার ভ্রামক () এবং কৌণিক বেগের () গুণফল থেকে পাওয়া যায়
নীলস বোরের পরমাণু মডেলে কোন শক্তি স্তরে ইলেকট্রনের কৌণিক ভরবেগ বের করা হয়েছিল।
![Physics Gurukul Logo [ cropped ]](https://bn.physicsgoln.com/wp-content/uploads/2022/05/cropped-Physics-Gurukul-Logo-300x300.jpg "কৌণিক ভরবেগ এবং জড়তার ভ্রামক 6 cropped Physics Gurukul Logo কৌণিক ভরবেগ এবং জড়তার ভ্রামক"){kind=logo}
জড়তার ভ্রামক
একটি কণার ভর ও ঘূর্ণন অক্ষ হতে এর লম্ব দূরত্বের বর্গের গুণফলকে উক্ত কণার জড়তার ভ্রামক বলে। বস্তুর মধ্যস্থিত সবগুলো কণার জড়তার ভ্রামকের সমষ্টিকে উক্ত বস্তুর জড়তার ভ্রামক বলে।
কোন অক্ষের চারদিকে ঘূর্ণায়মান কোন বস্তুর ওপর যে টর্ক প্রয়োগ করলে তাতে একক কৌণিক ত্বরণের সৃষ্টি হয় তাকে ওই অক্ষের সাপেক্ষে তার জড়তার ভ্রামক বলে।
একটা বস্তু সরলেরেখায় চললে ভরের যে ভূমিকা , কৌণিক গতিতে চললে জড়তার ভ্রামকের একই ভূমিকা।
মনেকরি, একটি বস্তু উল্লম্ব অক্ষ এর সাপেক্ষে ঘূর্ণরত।
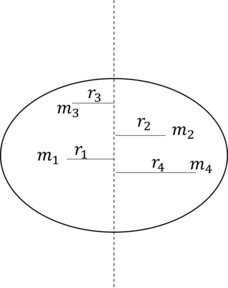
বস্তুটির একটি কণাটির ভর =
ঘূর্ণন অক্ষ হতে এর দূরত্ব =
সংজ্ঞা অনুযায়ী, কণাটির জড়তার ভ্রামক,
জড়তার ভ্রামক কণা বা কণাসমূহের তথা বস্তুর কৌণিক বেগের উপর নির্ভর করে না। এটি নির্ভর করে ঘূর্ণন অক্ষ সাপেক্ষে বস্তুর ভর বন্টনের উপর। কৌণিক বেগ কম বা বেশি হলে কৌণিক ভরবেগ ও গতিশক্তি কম বা বেশি হবে কিন্তু ঘূর্ণন অক্ষ সাপেক্ষে একটি বস্তুর জড়তার ভ্রামক অপরিবর্তিত থাকবে।
সুতরাং, সমগ্র বস্তুকণার জড়তার ভ্রামক,
বা,
ধরা যাক, ঘূর্ণনরত বস্তুটির মোট ভর = M; কল্পনা করা যাক, বস্তুটির সমস্ত ভর একটি বিন্দুতে কেন্দ্রীভূত আছে। ঘূর্ণন অক্ষ হতে ঐ বিন্দুর দূরত্ব K । K এর মান এমন যাতে, । কাল্পনিক এ দূরত্বকে চক্রগতির ব্যাসার্ধ বলা হয়।
কোন দৃঢ় বস্তুর সমগ্র ভর যদি একটি নির্দিষ্ট বিন্দুতে কেন্দ্রীভূত করা যায় যাতে করে একটি নির্দিষ্ট অক্ষের সাপেক্ষে ঐ কেন্দ্রীভূত বস্তুকণার জড়তার ভ্রামক, ঐ নির্দিষ্ট অক্ষের সাপেক্ষে সমগ্র দৃঢ় ঐ বস্তুর জড়তার ভ্রামকের সমান হয়, তাহলে ঐ নির্দিষ্ট অক্ষ থেকে কেন্দ্রীভূত বস্তুকণার লম্ব দূরত্বকে চক্ৰগতির ব্যাসার্ধ বলে।
তাৎপর্যঃকোন অক্ষের সাপেক্ষে কোন বস্তুর জড়তার ভ্রামক বলতে বােঝায় ঐ বস্তুর
প্রত্যেকটি কণার ভর এবং ঐ অক্ষ থেকে তাদের প্রত্যেকের লম্ব দূরত্বের বর্গের গুণফলের সমষ্টি ।
জড়তার ভ্রামক সংক্রান্ত দুটি উপপাদ্যের সাহায্যে কোন বস্তুর কোন একটি বিশেষ অক্ষের সাপেক্ষে জড়তার ভ্রামকের মান বের করা যায়। উপপাদ্য দুটি হল – (ক) লম্ব অক্ষ উপপাদ্য এবং (খ) সমান্তরাল অক্ষ উপপাদ্য।
(ক) লম্ব অক্ষ উপপাদ্য (Perpendicular axis Theorem)
বিবৃতিঃ কোন সমতল পাতের তলে অবস্থিত দুটি পরস্পর লম্ব অক্ষের সাপেক্ষে ঐ পাতের জড়তার ভ্রামকদ্বয়ের সমষ্টি হবে ঐ দূই অক্ষের ছেদবিন্দু দিয়ে এবং পাতের অভিলম্বভাবে গমনকারী অক্ষের সাপেক্ষে পাতটির জড়তার ভ্রামকের সমান।
অর্থাৎ,
(খ) সমান্তরাল অক্ষ উপপাদ্য (Parallel axis Theorem)
যে কোন অক্ষের সাপেক্ষে কোন বস্তুর জড়তার ভ্রামক হবে ঐ অক্ষের সমান্তরাল ও বস্তুর ভরকেন্দ্রের মধ্য দিয়ে গমনকারী অক্ষের সাপেক্ষে জড়তার ভ্রামক এবং ঐ বস্তুর ভর ও দুই অক্ষের মধ্যবর্তী লম্ব দূরত্বের বর্গের গুণফলের সমষ্টির সমান।
অর্থাৎ, ℎ2
ভরকেন্দ্রে সরল দন্ডের জড়তার ভ্রামক-{(1÷12)×ml^2} প্রান্তবিন্দুতে সরল দন্ডের জড়তার ভ্রামক-{(1÷3)×ml^2}
