আজকে আমরা প্রতিসরণাঙ্ক ও স্নেলের সূত্রের সাধারণ রূপ সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৬ জ্যামিতিক আলোকবিজ্ঞান এর অন্তর্ভুক্ত।
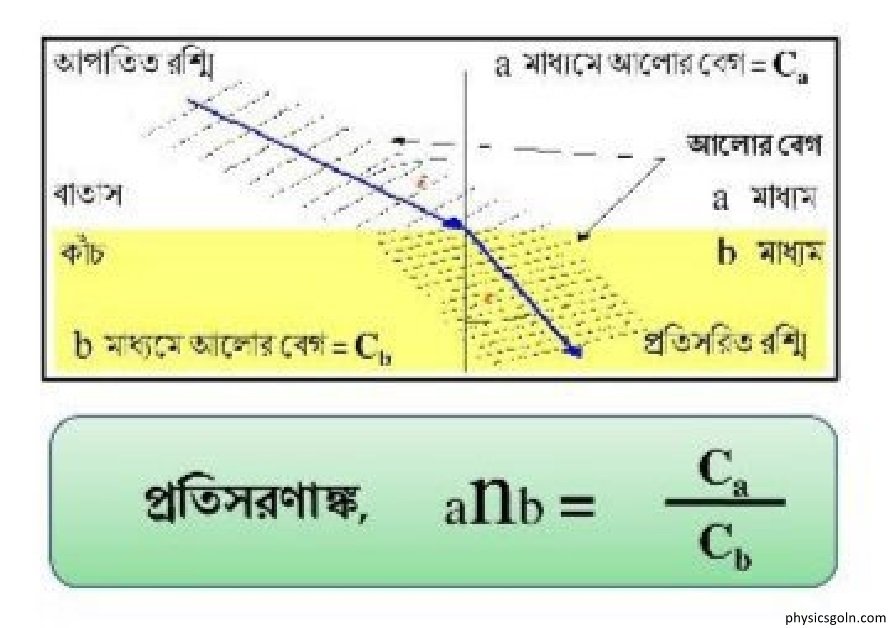
প্রতিসরণাঙ্ক ও স্নেলের সূত্রের সাধারণ রূপ
প্রতিসরণাঙ্ক (Refractive Index) :
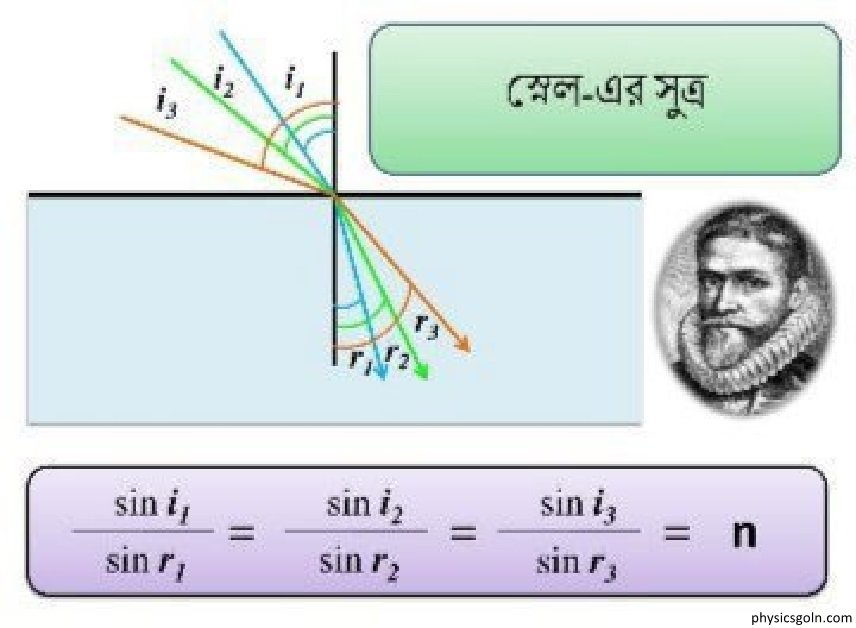
এক জোড়া নির্দিষ্ট স্বচ্ছ সমসত্ব মাধ্যম এবং তীর্যক ভাবে আপতিত নির্দিষ্ট বর্ণের একটি আলোকরশ্মির জন্য আপাতন কোণের সাইন ও প্রতিসরণ কোণের সাইনের অনুপাত একটি ধ্রব সংখ্যা। এই ধ্রব সংখ্যাকে প্রথম মাধ্যমের সাপেক্ষে দ্বিতীয় মাধ্যমের প্রতিসরণাঙ্ক বলে। যদি আলোকরশ্মি a মাধ্যমে i কোণে আপতিত হয়ে b মাধ্যমে r কোণে প্রতিসরিত হয় তবে a মাধ্যমের সাপেক্ষে b মাধ্যমে প্রতিসরণাঙ্ক, aμb = sini/sinr
বিভিন্ন মাধ্যমে আলোর বেগ বিভিন্ন। আমরা আলোর বেগের সাহায্যেও প্রতিসরণাঙ্কের সংজ্ঞায়িত করতে পারি ।
কোনো মাধ্যমের প্রতিসরাঙ্ক / হলে শূন্য মাধ্যমে আলোর বেগ এবং সেই মাধ্যমে আলোর বেগের অনুপাত ।
শূন্য মাধ্যমে আলোর বেগ c0 এবং সেই মাধ্যমে আলোর বেগের Cm হলে, μ = c0/Cm ……………….(1)
প্রতিসরণাঙ্ক দুই প্রকার, যথা-
১) আপেক্ষিক প্রতিসরণাঙ্ক ২) পরম প্রতিসরণাঙ্ক ।
আপেক্ষিক প্রতিসরণাঙ্ক (Relative Refractive Index) :
এক স্বচ্ছ সমসত্ব মাধ্যমের সাপেক্ষে অপর কোন স্বচ্ছ সমসত্ব মাধ্যমের প্রতিসরণাঙ্ককে প্রথম মাধ্যমের সাপেক্ষে দ্বিতীয় মাধ্যমের আপেক্ষিক প্রতিসরণাঙ্ক বলে। সাধারণত: a মাধ্যমের সাপেক্ষে b মাধ্যমে প্রতিসরণাঙ্ককে a দিয়ে লেখা হয়।
অর্থাৎ
aμb = sini/sinr ……………….(2)
Avgiv Rvwb, Av‡jvi MwZc cÖZveZ©bkxj (Reversible)। অর্থাৎ গতিপথের কোনো বিন্দু থেকে যদি 180° বিচ্যুতি ঘটানো যায় তবে আলো একই পথে ফিরে আসবে। সুতরাং আলোক রশ্মি যদি b মাধ্যম থেকে এসে বিভেদতলে অভিলম্বের সাথে । কোণে আপতিতন হয়ে ø মাধ্যমে। কোণে প্রতিসরিত হয় তবে b মাধ্যমের সাপেক্ষে a মাধ্যমে প্রতিসরণাঙ্ক
bμa = sinr/sini
myZivs aμb X bμa = sini/sinr X sinr/sini =1
ev, aμb = 1/bμa ……………….(3)

পরম প্রতিসরণাঙ্ক (Absolute Refractive Index) :
শূন্য মাধ্যমের সাপেক্ষে কোন স্বচ্ছ সমসত্ব মাধ্যমের প্রতিসরণাঙ্ককে ঐ মাধ্যমের পরম প্রতিসরণাঙ্ক বলে। স্পষ্টতঃ শূন্য স্থানের প্রতিসরণাঙ্ক 1।
কোনো মাধ্যমের প্রতিসরণাঙ্ক বলতে সাধারণত বায়ু মাধ্যমের সাপেক্ষে ঐ মাধ্যমের প্রতিসরণাঙ্ক বোঝায়। এটি মাধ্যমের পরম প্রতিসরণাঙ্ক নয়। শূন্য মাধ্যমের সাপেক্ষে বায়ু মাধ্যমের প্রতিসরণাঙ্ক μα = 1.002918 এবং বায়ুর সাপেক্ষে কাচে প্রতিসরণাঙ্ক 1.5।
সুতরাং কাচের পরম প্রতিসরণাঙ্ক μg =1.49956 এবং এই মানকে 1.5 ধরলে স্পষ্টত কোনো ত্র“টি হয় না । এই কারণে বায়ু মাধ্যমের সাপেক্ষে অন্য কোনো মাধ্যমের প্রতিসরণাঙ্ককে পরম প্রতিসরণাঙ্ক হিসাবে বিবেচনা করা হয়। কোনো মাধ্যমের পরম প্রতিসরণাঙ্ককে μ দিয়ে প্রকাশ করা হয়। একাধিক মাধ্যম থাকলে μ1,μ2,μ3 ইত্যাদি চিহ্ন দিয়ে প্রকাশ করা হয়। এমন কোনো মাধ্যমের অস্তিত্ব নেই যার μ <1।
পরম প্রতিসরণাঙ্ক ও আপেক্ষিক প্রতিসরণাঙ্কের মধ্যে পার্থক্য নীচে দেয়া হলো ।
পরম প্রতিসরণাঙ্ক | আপেক্ষিক প্রতিসরণাঙ্ক |
| ১) শূন্য মাধ্যমের সাপেক্ষে কোনো স্বচ্ছ সমসত্ব মাধ্যমের প্রতিসরণাঙ্ককে পরম প্রতিসরণাঙ্ক বলে। | ১) এক স্বচ্ছ সমসত্ব মাধ্যমের অপর কোন স্বচ্ছ সমসত্ব মাধ্যমের | প্রতিসরণাঙ্ককে আপেক্ষিক প্রতিসরণাঙ্ক বলে। |
| ২) শূন্য মাধ্যমে আলোক রশ্মি বিভেদ তলে অভিলম্বের সাথে i কোণে আপতিত হয়ে অপর কোন স্বচ্ছ সমসত্ব a মাধ্যমে r কোণে প্রতিসরিত হয় তবে পরম প্রতিসরণাঙ্ক, μa = sin i/ sin r | ২) a মাধ্যমে আলোক রশ্মি বিভেদ তলে অভিলম্বের সাথে i কোণে আপতিত হয়ে অপর কোন স্বচ্ছ সমসত্ব b মাধ্যমে r কোণে প্রতিসরিত হয় তবে আপেক্ষিক প্রতিসরণাঙ্ক, aμb = sini/sinr |
| ৩) শূন্য ও a মাধ্যমে আলোর বেগ যথাক্রমে Co ও Ca হলে পরম প্রতিসরণাঙ্ক, μa = Co/Ca | ৩) a ও b মাধ্যমে আলোর বেগ যথাক্রমে Ca ও Сь হলে প্রতিসরণাঙ্ক, aμb =Ca/Сь |
| ৪) আলোর তরঙ্গ দৈর্ঘ্য না বদলালে কোনো স্বচ্ছ মাধ্যমের পরম প্রতিসরণাঙ্ক প্রকৃতির উপর নির্ভর করে । | ৪) আলোর তরঙ্গ দৈর্ঘ্য না বদলালে কোনো স্বচ্ছ মাধ্যমের শুধু মাধ্যমের | আপেক্ষিক প্রতিসরণাঙ্ক মাধ্যম দুইটির প্রকৃতির উপর নিভর করে । |
| ৫) পরম প্রতিসরণাঙ্কের মান সর্বদাই একের চেয়ে বড় হয়। | ৫) আপেক্ষিক প্রতিসরণাঙ্কের মান একের চেয়ে বড় বা ছোট হতে পারে |
| ৬) পরম প্রতিসরণাঙ্ক সরাসরি নির্ণয় করা যায়। | ৬) a ও b মাধ্যমে পরম প্রতিসরণাঙ্ক যথাক্রমে যদি μa এবং μb হয় তবে a মাধ্যমের সাপেক্ষে b মাধ্যমের প্রতিসরণাঙ্ক = μb = μb/μa |
আপেক্ষিক প্রতিসরণাঙ্কের ব্যাখ্যা (Explanation of Relative Refractive Index) :
মনে করি বায়ু (a), পানি (w), ও কাচ (g) তিনটি স্বচ্ছ ভিন্ন মাধ্যম পরস্পর সমারাল ভাবে সজ্জিত আছে (চিত্র)। একটি এক বর্ণের আলোক PQ রশি¥ a ও w মাধ্যমে বিভেদ তলে অভিলম্বের সাথে । কোণে আপতিত হয়ে । কোণে QR পথে প্রতিসরিত হলো। এই প্রতিসরিত আলোক রশি¥ w ও g মাধ্যমের বিভেদ তলে অভিলম্বের সাথে ।” কোণে আপতিত হয়ে। কোণে RS পথে প্রতিসরিত হলো (যেহেতু a ও w এবং w ও g এর বিভেদ তলদ্বয় সমাড় রাল তাই অভিলম্বদ্বয়ও সমাাল)। এই প্রতিসরিত আলোক রশ্মি g ও a মাধ্যমের বিভেদ তলে অভিলম্বের সাথে।’ কোণে আপতিত হয়ে i কোণে ST পথে নির্গত হবে, কারণ PQ ও ST আলোক রশ্মি একই মাধ্যমে অবস্থিত তাই রশ্মিদ্বয় সমাাল।

চিত্রানুযায়ী, a মাধ্যমের সাপেক্ষে w মাধ্যমের প্রতিসরণাঙ্ক স্টেলের সূত্রানুসারে লেখা যায়, aμw = sini/sinr
অনুরূপভাবে w মাধ্যমের সাপেক্ষে g মাধ্যমের এবং g মাধ্যমের সাপেক্ষে a মাধ্যমের প্রতিসরণাঙ্ক যথাক্রমে,
wμg = sin r /sin r’ = এবং gμa = sin r’/ sin i
উপরের সমীকরণ তিনটিকে গুণ করে লেখা যায়,
aμw X wXg X gμa = sin i/ sin r X sin r’/ sin r X sin r’/sin i = 1
বা, aμw X wXg X 1/aμg =1 (যেহেতু gμa = 1/aμg)
সুতরাং, wμg = aμg/aμw ……………….(4)
(4) সমীকরণটি আপেক্ষিক প্রতিসরণাঙ্কের সমীকরণ নির্দেশ করে।
GLb a gva‡g Av‡jvi†eM ca n‡j a gva‡gicÖwZmiYv¼µa = Co/Са
Ges b gva tg Av‡jvi teM c, n‡j b gva‡gi cÖwZmiYv¼µb = Са/Сь
Zvn‡j, μb/μa = Ca/Сь ……………….(5)
(5) নং সমীকরণটি প্রমাণ করে কোনো মাধ্যমের পরম প্রতিসরণাঙ্ক ঐ মাধ্যমে আলোর বেগের ব্যানুপাতিক ।
Avevi, 4 সমীকরণ অনুসারে, aμb = μb/μa = Ca/Сь
ev, aμb = Ca/Сь ……………….(6)
Avevi, +matji mylvbymv‡i μb = sin i /sin r
myZivs Ca/Cb = sin i/sin r
ev, μasin i = μbsinr ……………….(7)
Avevi, aμb = sin i/sin r = μb/μa
ev, μa sini = μb sin r ……………….(8)
(8) সমীকরণটি স্নেলের সূত্রের সাধারণ রূপ নির্দেশ করে ।
সংকট কোণ ও পূর্ণ অভ্যীণ প্রতিফলন (Critical Angle and Total Internal Reflection):
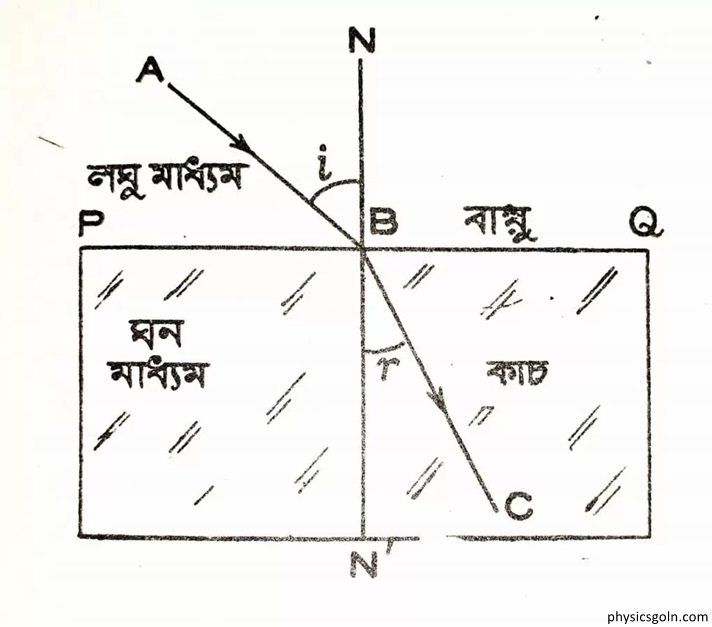
আলোক রশ্মি যখন ঘন মাধ্যম থেকে হালকা মাধ্যমে প্রবেশ করে তখন হালকা মাধ্যমে আলোক রশ্মি অভিলম্ব থেকে দূরে সরে যায়। তাই হালকা মাধ্যমে প্রতিসরণ কোণ সর্বদা আপতন কোণ অপেক্ষা বড় হয়। আপতন কোণ বাড়তে থাকলে প্রতিসরণ কোণও বাড়তে থাকে। ঘন মাধ্যমে আপতন কোণ বাড়তে বাড়তে এমন এক অবস্থায় আসে যখন প্রতিসরিত রশ্মি বিভেদতল দিয়ে গমন করে। অর্থাৎ প্রতিসরিত রশ্মি অভিলম্বের সাথে সমকোণে থাকে। ঘন মাধ্যমের এই কোণকে সংকট কোণ বলে। সংকট কোণকে সাধারণত ৪. প্রকাশ করা হয়। সংকট কোণের চেয়ে বড় কোণে আলোক রশ্মি ঘন মাধ্যমে আপতিত হলে আলোক রশ্মি বিন্দু মাত্র হালকা মাধ্যমে প্রতিসরিত না হয়ে বিভেদতল দিয়ে সম্পূর্ণরূপে প্রতি প্রতিফলিত হয়। একে পূর্ণ অভ্যীণ প্রতিফলন বলে ।

সংকট কোণঃ
এক জোড়া নির্দিষ্ট স্বচ্ছ সমসত্ব মাধ্যমের একটি নির্দিষ্ট বর্ণের আলোক রশ্মি ঘন মাধ্যমে অভিলম্বের সাথে যে কোণে অপতিত হলে প্রতিসরিত রশ্মি বিভেদ তল দ্বারা গমন করে, ঘন মাধ্যমের সেই কোণকে সংকট কোণ চিত্রে a হালকা মাধ্যম এবং b ঘন মাধ্যম। মনে করি ঘন মাধ্যমে PO2 আলোক রশ্মি O2 বিন্দুতে অংকিত অভিলম্বের সাথে বলে। সংকট কোণকে সাধারণতঃ ৪. প্রকাশ করা হয়।
8c †কাণে আপতিত হওয়ায় বিভেদ তল দিয়ে O2Q2 পথে অভিলম্বের সাথে 90° প্রতিসরিত হলো।
প্রতিসরণের সূত্রানুসারে, aμb = sin i/ sin r
বা, aμb = sin 90/ sin8c
বা, aμb = 1/ sin8c ……………….(9)
এটাই প্রতিসরণাংকের সাথে সংকট কোণের সম্পর্ক।
পূর্ণ অভ্যীণ প্রতিফলন (Total Internal Reflection) :
এক জোড়া নির্দিষ্ট স্বচ্ছ সমসত্ব মাধ্যমে একটি নির্দিষ্ট বর্ণের আলোক রশ্মি ঘন মাধ্যম থেকে হালকা মাধ্যমে যাবার সময় যদি দুই মাধ্যমের বিভেদ তলে সংকট কোণের চেয়ে বড় কোণে আপতিত হয় তবে আলোক রশ্মি হালকা মাধ্যমে বিন্দুমাত্র প্রতিসৃত না হয়ে সম্পূর্ণরূপে বিভেদ তল দ্বারা ঘন মাধ্যমে প্রতিফলিত হয়। একে পূর্ণ অভ্যীণ প্রতিফলন বলে ।
পূর্ণ অভ্যীণ প্রতিফলনের শর্ত ঃ-
পূর্ণ অভ্যীণ প্রতিফলনের শর্ত দুইটি ।
১। আলোক রশ্মি অবশ্যই ঘন মাধ্যম থেকে হালকা মাধ্যমের দিকে যেতে হবে।
২। এক জোড়া নির্দিষ্ট সচ্ছ সমসত্ব মাধ্যম ও একটি নির্দিষ্ট বর্ণের আলোক রশ্মিকে সংকট কোণের চেয়ে বড় কোণে আপতিত হতে হবে।
উদাহরণ-১:
একটি স্বচ্ছ মাধ্যমের প্রতিসরণাঙ্ক 1.65 হলে ঐ মাধ্যমে আলোর বেগ বের করন। শূন্যস্থানে আলোর বেগ, Co = 3×108 ms-1
সমাধান:
দেয়া আছে,
μ=1.65, co =3×10 ms-1 এবং v =?
আমরা জানি,
μ = Co/Cm
বা, Cm = Co/μ = (3×108)/1.65 = =1.82×108ms-1
উত্তর: 1.82×108 ms -1
উদাহরণ ২:
কাচের ও পানির প্রতিসরণাঙ্ক যথাক্রমে 3/2 এবং । পানির সাপেক্ষে কাচের প্রতিসরণাঙ্ক বের করন।
সমাধানঃ
দেয়া আছে, aμg = 3/2, aμw = 4/3, wμg = ?
আমরা জানি,
wμg = aμg/aμw
অতএব,
wμg = 3/2 x 3/4 = 9/8
উ: 9/8
উদাহরণ ৩:
পানির প্রতিসরণাঙ্ক হলে পানির সংকট কোণ বের করন।
সমাধানঃ
দেয়া আছে, μ = 4/3, 8c = ?
আমরা জানি, μ = 1/ sin8c
বা, sin8c = 1/μ = 3/4 = 0.75
বা, sin8c = sin-1 0.75 = 48.6°
উ: 48.6°
সার-সংক্ষেপ :
প্রতিসরণাঙ্কঃ
এক জোড়া নির্দিষ্ট স্বচ্ছ সমসত্ব মাধ্যম এবং তীর্যক ভাবে আপতিত নির্দিষ্ট বর্ণের একটি আলোকরশ্মির জন্য আপাতন কোণের সাইন ও প্রতিসরণ কোণের সাইনের অনুপাত একটি ধ্র“ব সংখ্যা। এই ধ্র“ব সংখ্যাকে প্রথম মাধ্যমের সাপেক্ষে দ্বিতীয় মাধ্যমের প্রতিসরণাঙ্ক বলে।
পরম প্রতিসরণাঙ্কঃ
শূন্য মাধ্যমের সাপেক্ষে কোন স্বচ্ছ সমসত্ব মাধ্যমের প্রতিসরণাঙ্ককে ঐ মাধ্যমের পরম প্রতিসরণাঙ্ক বলে।
আপেক্ষিক প্রতিসরণাঙ্কঃ
এক স্বচ্ছ সমসত্ব মাধ্যমের সাপেক্ষে অপর কোন স্বচ্ছ সমসত্ব মাধ্যমের প্রতিসরণাঙ্ককে প্রথম মাধ্যমের সাপেক্ষে দ্বিতীয় মাধ্যমের আপেক্ষিক প্রতিসরণাঙ্ক বলে।
সংকট কোণঃ
এক জোড়া নির্দিষ্ট স্বচ্ছ সমসত্ব মাধ্যমের একটি নির্দিষ্ট বর্ণের আলোক রশ্মি ঘন মাধ্যমে অভিলম্বের সাথে যে কোণে অপতিত হলে প্রতিসরিত রশ্মি বিভেদ তল দ্বারা গমন করে, ঘন মাধ্যমের সেই কোণকে সংকট কোণ বলে ।
পূর্ণ অভ্যরীণ প্রতিফলনঃ
এক জোড়া নির্দিষ্ট স্বচ্ছ সমসত্ব মাধ্যমে একটি নির্দিষ্ট বর্ণের আলোক রশ্মি ঘন মাধ্যম থেকে হালকা মাধ্যমে যাবার সময় যদি দুই মাধ্যমের বিভেদ তলে সংকট কোণের চেয়ে বড় কোণে আপতিত হয় তবে আলোক রশ্মি হালকা মাধ্যমে বিন্দুমাত্র প্রতিসৃত না হয়ে সম্পূর্ণরূপে বিভেদ তল দ্বারা ঘন মাধ্যমে প্রতিফলিত হয়। একে পূর্ণ অভ্যীণ প্রতিফলন বলে ।
বহুনির্বাচনী প্রশ্ন:
নীচের উদ্দীপকটি পড়ুন এবং ১ ও ২ নং প্রশ্নের উত্তর দিন।
একটি কাচের শ্টাব পানিতে নিমজ্জিত আছে। দেয়া আছে ag = 1.5 এবং a = 1.33
১। কাচ ও পানির বিভেদতলে একটি আলোক রশ্মির জন্য সংকট কোণ কত?
ক. 44.8 °
খ. 52.7″
গ. 56.7°
ঘ. 62.5″
২। পানিও বায়ুর বিভেদতলে একটি আলোক রশ্মির জন্য সংকট কোণ কত?
ক. 44.8 °
খ. 52.7°
গ. 56.7°
ঘ. 62.5°
