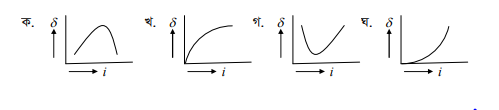প্রিজমে আলোর প্রতিসরণ

আজকে আমরা প্রিজমে আলোর প্রতিসরণ সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৬ জ্যামিতিক আলোকবিজ্ঞান এর অন্তর্ভুক্ত।

প্রিজমে আলোর প্রতিসরণ

প্রিজম (Prism):

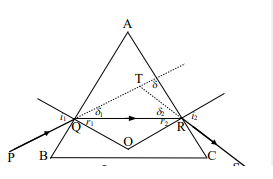
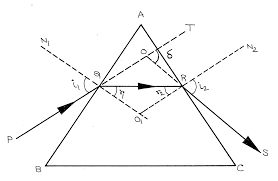
আলোকবিজ্ঞানে প্রিজম বলতে পরস্পরের সাথে আনত অদ্ভূত দুটি মসৃণ সমতল দিয়ে আবদ্ধ যে কোনো স্বচ্ছ মাধ্যমের অংশকে বোঝায়। এই তলগুলোকে বলা হয় প্রিজমের প্রতিসারক তল (refracting surface)। তলদুটির অনতি কোণকে প্রিজমের প্রতিসারক কোণ (refracting angle of the prism) বা সংক্ষেপে প্রিজম কোণ (angle of the prism) বলে। প্রতিসারক তলদ্বয় যে সরলরেখায় ছেদ করে তাকে প্রিজমের ধার ( edge of the prism) বলে। (৬.১৩) চিত্রে দেখানো প্রিজমের MPQN এবং MPRO প্রতিসারক তলদ্বয় MP ধার-এ মিলিত হয়েছে। ZNMO অথবা <PRQ হলো প্রতিসারক কোণ। N 2 প্রতিসারকের ধারের সাথে সমকোণে অবস্থিত যে কোনো সমতল ছেদকে প্রিজমের প্রধান ছেদ (principal section)। (৬.১৩) চিত্রে ABC হলো প্রধান ছেদ।

প্রিজমের প্রধান ছেদে আলোক রশ্মির গতিপথ ও ন্যূনতম বিচ্যুতি (Path of the Ray in the Principal section of a Prism and Minimum Daviation):

মনে করি ABC একটি প্রিজমের প্রধান ছেদ এবং A হলো প্রিজমের শীর্ষ কোণ বা প্রিজম কোণ। ABC প্রিজমের AB প্রতিসারক তলে PQ একটি আলোক রশ্মি Q বিন্দুতে অভিলম্বের সাথে i; কোণে আপতিত হয়ে ঘন মাধ্যমে ।; কোণে প্রতিসরিত হয়ে QR পথে গমন করে এবং পূর্ববর্তী রশ্মির সাথে ৪, কোণে বিচ্যুত হয়। এই প্রতিসরিত আলোক রশ্মি AC

প্রতিসারক তলে R wবন্দুতে অভিলম্বের সাথে 12 কোণে আপতিত হয়ে হালকা মাধ্যমে i, কোণে প্রতিসরিত হয়ে RS পথে নির্গত হয় এবং পূর্ববর্তী QR রশ্মির সাথে ঠ, কোণে বিচ্যুত হয়। সুতরাং, আপতিত রশ্মি PQ এর সাথে নির্গত রশ্মি RS এর মোট বিচ্যুতি 8 হলে,

81 +82=8 ………………………….(1)

[ত্রিভূজের বহিঃস্থ কোণ অস্থ বিপরীত কোণদ্বয়ের যোগফলের সমান]

চিত্রানুসারে, ∆QOR এর r1 + r2 + ∠QOR = π ………………………….(2)

আবার ∆QOR চতুর্ভুজের ∠A + ∠AQO + ∠QOR + ∠ARO = 2π

কিন্তু ∠AQO = ∠ARO = л/2 [QO এবং RO প্রতিসারক তলের উপর লম্ব ]

:. ∠A + ∠OOR = л ………………………….(3)

(2) এবং (3) সমীকরণ থেকে লেখা যায়, ri + r2 +∠QOR = ∠A + ∠QOR

বা, r1 + r2 = A …………………………(4)

আবার চিত্রানুসারে, i1 = r1 + 81 এবং i2 = r2 + 82 [বিপ্রতীপ কোণ বলে]

i1 + 12 = r1 + r2 + 81 + 82

উপরের সমীকরণটিকে (1) ও (4) নং সমীকরণের সাহায্যে লেখা যায়,

i1+i₂ = A + 8 …………………………(5)

প্রিজমের বিচ্যুতি কোণ (8) এর মান আপাতন কোণ (i1) এর উপর নির্ভর করে। আপাতন কোণ খুব ছোট হলে বিচ্যুতি কোণ বড় হয়। আপতন কোণ বাড়তে থাকলে বিচ্যুতি কোণ কমতে থাকে। বিচ্যুতি কোণের মান আপতন কোণের সাপেক্ষে কমতে কমতে একটি সর্বনিম্ন মানে পৌছানোর পর আপতন কোণ বৃদ্ধির সাথে সাথে বিচ্যুতি কোণ বাড়তে শুর করে। বিচ্যুতি কোণের এই সর্বনিম্ন মানকে সর্বনিম্ন বিচ্যুতি বলে। একে সূচিত করা হয়। (৬.১৫) নং i-6 লেখচিত্রে আপতন কোণের সাপেক্ষে বিচ্যুতি কোণের পরিবর্ত এবং সর্বনিম্ন বিচ্যুতি দেখানো হয়েছে।

(5) নং সমীকরণকে বর্গ করে পাই, (A + 8)2 = (i1+i2)2

বা, (A + 8)2 = (i1 – i2) + 4i1i2 ………………………..(6)

(6) নং সমীকরণে ৪ = 8m হলে বাম পক্ষের মান সর্বনিম্ন হবে। ডান পক্ষের মান সর্বনিম্ন হতে হলে (i1 -i2) = 0 হতে হবে,

তাহলে, যখন 8 = 8m তখন i1 – i2 = 0

অর্থাৎ i1 = i2 = i (ধরি ) ………………………..(7)

প্রতিসরণের সূত্রানুসারে, μ = sini1/sinr1 = sini2/sinr2

বা, sini1/sini2 = sinri/sinr2

(7) নং সমীকরণের মান বসালে, sinri/sinr2 =1

বা, sinri = sinr2

অর্থাৎ

ri = r2 =r (ধরি) ………………………..(8)

সুতরাং প্রিজমের সাপেক্ষে যখন আপতিত রশ্মি ও নির্গত রশ্মি প্রতিসাম্য ভাবে অবস্থিত থাকে অর্থাৎ যখন আপতন কোণ ও নির্গত কোণ সমান হয় তখন সর্বনিম্ন বিচ্যুতি ঘটে ।

(7) ও (8) নং সমীকরণের সর্বনিম্ন বিচ্যুতি শর্তগুলি (6) ও (5) নং সমীকরণে বসালে, i1 + i2 =i+i=2i= A +8m

বা, i= A+8m/ 2 ………………………..(9)

এবং r1 +r2 = r+r = 2r = A

বা, r = A/2 ………………………..(10)

প্রতিসরণের সূত্রানুসারে,  μ = sini/sinr

এখন (9) এবং (10) নং সমীকরণে i এবং r এর মান বসালে,

μ = {sin( A+8m)/2}/ 2 sinA/2 ………………………..(11)

(11) নং সমীকরণ হলো প্রিজমের প্রতিসরাংকের সাথে সর্বনিম্ন বিচ্যুতির সম্পর্ক।

 সর— প্রিজম এবং এর প্রতিসরাংকের সাথে বিচ্যুতি কোণের সম্পর্ক

যে প্রিজমের প্রতিসারক কোণ অত্যন্ড্র ক্ষুদ্র (10° এর নীচে) তাকে সর বা পাতলা প্রিজম বলে।

সর প্রিজমের আলোক রশ্মি যে কোন প্রতিসারক তলে প্রায় অভিলম্ব বরাবর আপতিত হয় অর্থাৎ আপতন কোণ i1 অত্যন্ড্র ক্ষুদ্র হয় ফলে প্রতিসরণ কোণ r1 ও r2 খুব ক্ষুদ্র হয়। (কারণ r1 + r2 = A এবং A < 10°)

আবার আমরা জানি ক্ষুদ্র হলে sin8 = 8 হয়।

সর— প্রিজমের ক্ষেত্রে প্রথম প্রতিসারক তলে প্রতিসরণের সূত্রানুসারে, μ= sin i1 /sinr1 =  i1 /r1

(কারণ ৪ খুব ছোট হলে sin 0 = 0 হয়)

বা, i1 = μr1 ………………………..(12)

এবং দ্বিতীয় প্রতিসারক তলে প্রতিসরণের সূত্রানুসারে, μ= sin i2 /sinr2 =  i2 /r2

বা, i2 = μr2 ………………………..(13)

আবার (5) নং সমীকরণ থেকে পাই, i1 + i2 =A+8

(12) ও (13) নং সমীকরণ থেকে পাই, μ(r1 + r2) =A+8

আবার, (4) নং সমীকরণের সাহায্যে লেখা যায়, μA – A = 8 (যেহেতু r1 + 12 = A)

বা, 8 =(μ-1)A ………………………..(14)

এটাই সর— প্রিজমের প্রতিসরণাংকের সাথে বিচ্যুতি কোণের সম্পর্ক।

উদাহরণ ১:

একটি সমবাহু প্রিজমের প্রতিসরণাঙ্ক 1.5 হলে এর ন্যূনতম বিচ্যুতি কোণ বের করন।

সমাধানঃ

দেয়া আছে, A = 60, μ = 1.5 এবং 8m =?

আমরা জানি,

μ = {sin( A+8m)/2}/  sinA/2

gvb emvtj, 1.5= {sin( 60°+8m)/2}/  sin60°/2 = {sin( 60°+8m)/2}/  sin30°

{sin( 60°+8m)/2}/0.5

ev, {sin( 60°+8m)/2}/2

= 1.5 x 0.5 = 0.75

= 60°+8m)/2sin-1 0.75

= 48.59°

ev8m sin-1 0.75 = 48.59° x 2-60° = 37.18°

AZGe  wePz wZ 37.18°

উ: 37.18°

উদাহরণ ২:

একটি প্রিজমের প্রতিসরণাঙ্ক 1.5 এবং me©wbga wePzwZ 38 ° হলে এর প্রিজম কোণ নির্ণয় করন। সমাধানঃ দেয়া আছে, A = 60, μ = 1.5, 8m = 38° এবং A = ?

আমরা জানি,

μ = {sin( A+8m)/2}/  sinA/2

gvb emvtj, 1.5 = {sin( A+38)/2}/  sinA/2

= {sin( A/2+19)}/  sinA/2

= {sin( A/2+cos 19°)} + cosA/2sin 19°/  sinA/2

ev, 1.5 =  {0.95 sinA/2+0.33 cos A/2}/ sinA/2

= 0.95+0.33 cotA/2

ev, cotA/2 = (1.5-0.95°)/0.33

= 1.67

ev, cot-¹1.67 = 30.9°

ev, A=61.8°

D: wcÖRg †KvY 61.8″

উদাহরণ ৩:

একটি সর— প্রিজমের প্রিজম কোণ 6° এবং প্রতিসরণাঙ্ক 1.5 । বিচ্যুতি কোণ বের করন।

সমাধানঃ

দেয়া আছে, A=6°,u= 1.5 এবং 6 =?

আমরা জানি, 6 =(u− 1 ) A

মান বসালে, 6 = (1.5-1)6° =3°

সুতরাং বিচ্যুতি কোণ 3°।

উ: 3°

সার-সংক্ষেপ :

 সর্বনিম্ন বিচ্যুতি:

আপাতন কোণ খুব ছোট হলে বিচ্যুতি কোণ বড় হয়। আপতন কোণ বাড়তে থাকলে বিচ্যুতি কোণ কমতে থাকে। বিচ্যুতি কোণের মান আপতন কোণের সাপেক্ষে কমতে কমতে একটি সর্বনিম্ন মানে পৌছানোর পর আপতন কোণ বৃদ্ধির সাথে সাথে বিচ্যুতি কোণ বাড়তে শুর“ করে। বিচ্যুতি কোণের এই সর্বনিম্ন মানকে সর্বনিম্ন বিচ্যুতি বলে।

প্রিজমের প্রতিসরণাঙ্কের সাথে সর্বনিম্ন বিচ্যুতির সম্পর্ক,

μ = {sin( A+8m)/2}/  sinA/2

wcÖRg†KvYJz© n‡j, S = (u – 1 ) A

বহুনির্বাচনী প্রশ্ন:

১। একটি সমদ্বিবাহু ও সমকোণী প্রিজমের অতিভূজ ছাড়া অন্য যে কোনো প্রতিসারক তলে একটি আলোক রশ্মি লম্ব ভাবে আপতিত হলে অপর প্রতিসারক তল দিয়ে কত কোণে নির্গত হবে?

ক. 0°

খ. 45°

গ. 90°

ঘ. 180 °

২। নীচের কোন লেখটি আপাতন কোণ ও বিচ্যুতি কোণের সম্পর্ক নির্দেশ করে?