স্বকীয় আবেশ ও পারস্পরিক আবেশ

আজকে আমরা স্বকীয় আবেশ ও পারস্পরিক আবেশ সম্পর্কে আলোচনা করবো। যা বাউবি এইচএসসি ২৮৭১ পদার্থ বিজ্ঞান ২য় পত্র ইউনিট ৪ তাড়িতচৌম্বক আবেশ ও দিক পরিবর্তী প্রবাহ এর অন্তর্ভুক্ত।

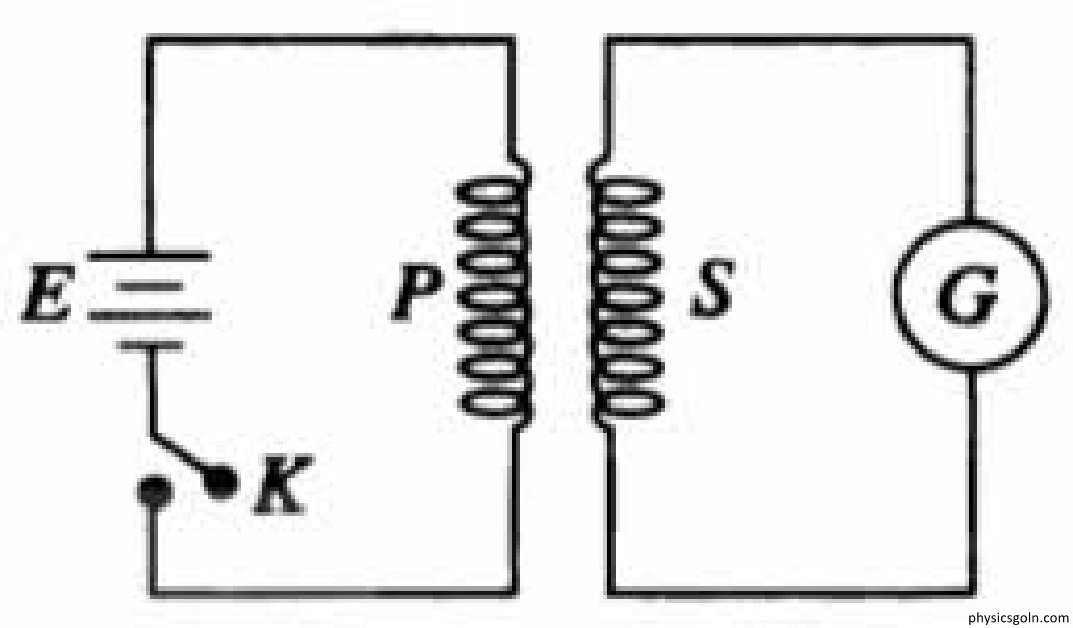
স্বকীয় আবেশ ও পারস্পরিক আবেশ

 স্বকীয় আবেশ (Self Induction)

যখন কোনো তার-কুলীর মধ্য দিয়ে তড়িৎ প্রবাহ পাঠানো হয়, তখন ঐ প্রবাহ একটি চৌম্বক ক্ষেত্র উৎপন্ন করে এবং চৌম্বক ক্ষেত্রের বলরেখাগুলো কু-লীটির বিভিন্ন পাকের সাথে জড়িয়ে পড়ে [চিত্র]। সুতরাং বলা যায়, ঐ কুলীতে তড়িৎ প্রবাহ শুর হওয়ার সময়, কুলী হঠাৎ নিজস্ব চৌম্বক বলরেখার সাথে জড়িত হয় এবং এর ফলে, কুলীতে একটি ক্ষণস্থায়ী বিপরীতমুখী তড়িচ্চালক শক্তি আবিষ্ট হয়ে প্রবাহমাত্রা বৃদ্ধিতে বাধা সৃষ্টি করে।

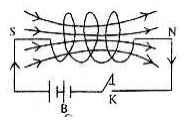
আবার কুলীতে তড়িৎ প্রবাহ বন্ধ করলে কুন্ডলীর সাথে জড়িত নিজস্ব চৌম্বক ক্ষেত্রের বলরেখাগুলো হঠাৎ অপসারিত হয় অর্থাৎকুলীর সাথে জড়িত বলরেখার পরিবর্তন ঘটে। তখন আবার কুলীতে একটি সমমুখী ক্ষণস্থায়ী তড়িচ্চালক শক্তি আবিষ্ট হয় এবং এর ফলে কুলীতে তড়িৎ s প্রবাহের অবলুপ্তি বিলম্বিত হয়।

অনুরূপভাবে, কুলীতে তড়িৎ প্রবাহ চালু থাকাকালীন যদি প্রবাহমাত্রার পরিবর্তন (হ্রাস বা বৃদ্ধি) করা হয়, তাহলে কুলীর সাথে জড়িত নিজস্ব চৌম্বক ক্ষেত্রের বলরেখার পরিবর্তন হয় এবং সাথে সাথে কুলীতে একটি ক্ষণস্থায়ী তড়িচ্চালক শক্তি উৎপত্তি হয়ে প্রবাহমাত্রার ঐ পরিবর্তনকে বাধা দেয়।

উপরোক্ত ক্ষেত্রসমূহ উৎপন্ন তড়িচ্চালক শক্তিকে বলা হয় স্বকীয় আবেশের কারণে আবিষ্ট ‘তড়িচ্চালক শক্তি’ (self induced e.m.f.)। তড়িৎ বর্তনীর যে ধর্মের ফলে ঐ বর্তনী প্রবাহমাত্রার পরিবর্তনের বির“দ্ধে বাধা সৃষ্টি করে তাকে ‘স্বকীয় আবেশ ধর্ম’ (self inductance) বলে এবং উপরিউক্ত ঘটনাকে বলা হয় স্বকীয় আবেশ (self induction) কুলীটিকে বলা হয় আবেশক (inductor)।
[প্রবাহমাত্রা স্থির থাকলে তড়িচ্চালক শক্তি আবিষ্ট হয় না ।]

সংজ্ঞাঃ

কোনো বর্তনীর নিজ প্রবাহের দ্বারা সৃষ্ট চৌম্বক ক্ষেত্রের মাত্রা পরিবর্তনের ফলে বর্তনীতে একটি তড়িচ্চালক শক্তি আবিষ্ট হয়। এ ঘটনা হল স্বকীয় আবেশ।

স্বকীয় আবেশযুক্ত বর্তনীকে বলা হয় ‘আবেশী বর্তনী’ (inductive circuit)।

পারস্পরিক আবেশ (Mutual Induction)

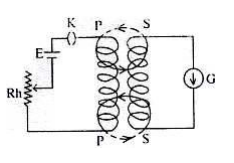
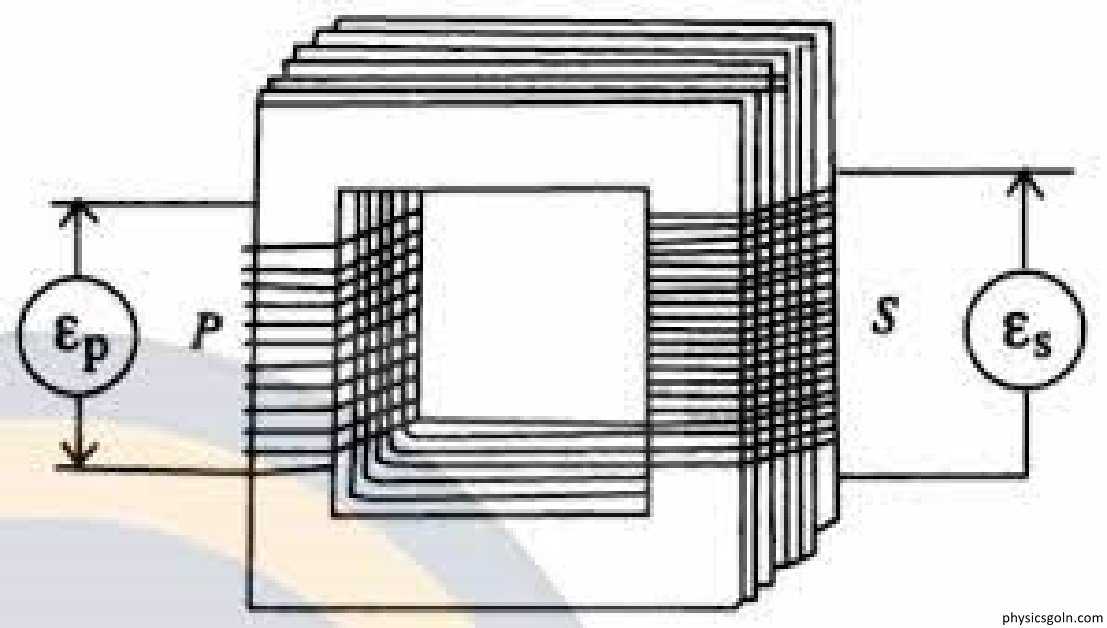
একটি কুলীতে তড়িৎ প্রবাহের পরিবর্তনের ফলে এর কাছাকাছি অবস্থিত অপর একটি কুলীতে আবিষ্ট তড়িচ্চালক শক্তির উদ্ভব হয় চিত্র]। দ্বিতীয় কুলীতে ফ্লাক্সের পরিবর্তনের ফলে এটি ঘটে।

প্রথম কুলীটিকে বলা হয় মুখ্য কুলী (primary coil) এবং দ্বিতীয়টিকে, অর্থাৎ যার মধ্যে তড়িচ্চালক শক্তি আবিষ্ট হয়, তাকে বলা হয় গৌণ কুলী ( secondary coil)। মুখ্য কুলীতে (PP) তড়িৎ প্রবাহ চালু করলে একটি চৌম্বক ক্ষেত্র সৃষ্টি হয়। ফলে চৌম্বক বলরেখার উৎপত্তি ঘটে। উৎপন্ন এ বলরেখাগুলো গৌণ কুলীর (SS) সাথে জড়িয়ে পড়ে ।

পাশাপাশি স্থাপিত দুটি কুলীর যেকোনো একটিতে তড়িৎ প্রবাহের পরিবর্তন ঘটলে অপরটিতে তড়িচ্চালক শক্তি আবিষ্ট হয়, এ ঘটনাকে পারস্পরিক আবেশ বলে।

আবেশ গুণাঙ্ক: স্বকীয় আবেশ গুণাঙ্ক (Coefficient of Self induction)

কোনো তার-কুলীর মধ্য দিয়ে বিদ্যুৎ প্রবাহিত হলে একটি চৌম্বক ক্ষেত্রের সৃষ্টি হয়। সৃষ্ট বলরেখার সংখ্যা তথা চৌম্বক ফ্লাক্স (φ) কুলীর মধ্য দিয়ে বিদ্যুৎ প্রবাহমাত্রার (I) সমানুপাতিক । অর্থাৎ,

φ α I

এ ফ্লাক্স কুলীর প্রতিটি পাকের সাথে জড়িত। কুলীর পাক সংখ্যা N হলে, কুলীর ফ্লাক্স সংযুক্তি (Flux linkage) বা মোট ফ্লাক্স হবে Nφ । সমীকরণ, (1) হতে,

Nφ α I

বা, Nφ = LI …………………(2)

এখানে, L একটি সমানুপাতিক ধ্রুবক। একে কুলীর স্বকীয় আবেশ গুণাঙ্ক বা স্বাবেশ গুণাঙ্ক বলা হয়। L এর মান কুলীর আকার, পাক সংখ্যা ইত্যাদির উপর নির্ভর করে। একটি নির্দিষ্ট কুলীর জন্য এটি ধ্রুবক।

(2) নং সমীকরণ হতে দেখা যায় যে, যখন I = l একক হয় তখন,

Nφ = L

অতএব, Lকে নিম্নরূপে সংজ্ঞায়িত করা যায়:

কোনো কুলীতে প্রবাহমাত্রা এক একক হলে, ঐ কুলীর সাথে জড়িত মোট ফ্লাক্স সংখ্যাগতভাবে এর স্বকীয় আবেশ গুণাঙ্কের সমান ।

আবিষ্ট তড়িচ্চালক শক্তিঃ

ফ্যারাডের সূত্র অনুসারে, আবিষ্ট তড়িচ্চালক শক্তি,

ε α -(d/dt)(Nφ)

= -d(d/dt)(LI)

বা, ε α –L(dl/dt) …………………(3)

(3) নং সমীকরণের ঋণাত্মক চিহ্ন এটাই বুঝাচ্ছে যে, আবিষ্ট তড়িচ্চালক শক্তি সর্বদা প্রবাহমাত্রার পরিবর্তনের বিরোধিতা করে, অর্থাৎ প্রবাহমাত্রা বৃদ্ধি পেলে এটি এর বৃদ্ধির বিরোধিতা করবে; আবার হ্রাস পেতে থাকলে, এটি ঐ হ্রাসের বির“দ্ধে কাজ করবে। ৪.৬ নং সমীকরণ অনুসারে,

L= – ε /(dI/dt) …………………(4)

উপরের সমীকরণটির মাধ্যমে স্বকীয় আবেশ গুণাঙ্কের বিকল্প সংজ্ঞা দেয়া যায়। সংজ্ঞাটি নিম্নরূপ :

এ সমীকরণে, dI/dt = 1 হলে ε = -L হয়। কাজেই, কোনো বর্তনীতে একক হারে প্রবাহমাত্রার পরিবর্তন হলে বর্তনীতে যে
তড়িচ্চালক শক্তি আবিষ্ট হবে সংখ্যাগতভাবে তা ঐ বর্তনীর স্বকীয় আবেশ গুণাঙ্কের সমান।

[ধারকের সংখ্যা তড়িৎ ক্ষেত্রের উপস্থিতির মতো আবেশকের (inductor) মধ্যে চৌম্বক ক্ষেত্রের উপস্থিতি বিশেষ তাৎপর্যপূর্ণ।]

স্বকীয় আবেশ গুণাঙ্কের একক

4 নং সমীকরণ অনুসারে, স্বকীয় আবেশ গুণাঙ্কের একক হচ্ছে,

V/As

বা, Vs/A

বা, VsA-1

এই একককে henry (H) নামে অভিহিত করা হয়।

1 H = 1 VsA-1 …………………(5)

কোনো কুলীতে প্রতি সেকে-ে 1 A হারে প্রবাহমাত্রার পরিবর্তন হলে যদি 1 V তড়িচ্চালক বল আবিষ্ট হয় তাহলে ঐ কুলীর স্বকীয় আবেশ গুণাঙ্ক হবে 1 henry।

henry এককটি বড় একক বলে সাধারণত milli henry (mH) এবং micro henry (UH) একক ব্যবহার করা হয়।

1mH = 10-3H

1uu = 10-6H

আবার, 2 নং সমীকরণ অনুসারে, স্বকীয় আবেশ গুণাঙ্কের একক হচ্ছে,

1H = 1 VsA-1 = 1 WbA-1 …………………(6)

পারস্পরিক আবেশ গুণাঙ্ক বা আবেশাঙ্ক (Coefficient of mutual induction or mutual inductance)

ধরা যাক, দুটি কুলী পাশাপাশি অবস্থিত (চিত্র) PP মুখ্য কুলী, SS গৌণ কুলী। এদের পাক সংখ্যা যথাক্রমে
N1 ও N2 |

ধরি, PP কুলীর মধ্য দিয়ে I তড়িৎ প্রবাহের ফলে সৃষ্ট চৌম্বক ক্ষেত্রের জন্য SS কুলীতে ফ্লাক্স =φ2 । φ2 পরিমাণ ফ্লাক্স গৌণ কুলীর প্রতিটি পাকের সাথে জড়িত হয়। অতএব, গৌণ কুলীতে মোট ফ্লাক্স সংযুক্তি =N2φ2। মুখ্য কুলীতে তড়িৎ প্রবাহ চললে গৌণ কুলীর সাথে জড়িত মোট ফ্লাক্স প্রবাহমাত্রার সমানুপাতিক হয়, অর্থাৎ,

N2 φ2 ∝ I1

বা, N2 φ2 = MI1

বা, M= N2φ2/I1 …………………(7)

এখানে, M একটি সমানুপাতিক ধ্রুবক। একে কুলীদ্বয়ের পারস্পরিক আবেশ গুণাঙ্ক বলে। M এর মান গৌণ কুলীর পাকসংখ্যা, কুলীদ্বয়ের মধ্যবর্তী দূরত্ব, আপেক্ষিক অবস্থান ও আকারের উপর নির্ভর করে।

আবিষ্ট তড়িচ্চালক শক্তি

ফ্যারাডের সূত্র অনুসারে, গৌণ কুলীতে আবিষ্ট তড়িচ্চালক শক্তি,

ε2 = -(d/dt)N2φ2 = – -(d/dt) (MI1) = – M (dI/dt)

বা, M=- ε2 /(dI1/dt)

(6) এবং (7) নং সমীকরণের সাহায্যে আমরা M-কে সংজ্ঞায়িত করতে পারি:

(ক) দুটি কুলীর মধ্যে একটিতে একক তড়িৎ প্রবাহের জন্য দ্বিতীয়টির সাথে যে মোট চৌম্বক ফ্লাক্স জড়িত হয়, তার সংখ্যাগত মান কুলী দুটির পারস্পরিক আবেশাঙ্কের সমান ।

(খ) দুটি কুলীর মধ্যে একটির মধ্য দিয়ে প্রবাহমাত্রার পরিবর্তনের হার একক হলে দ্বিতীয় কুলীতে যে তড়িচ্চালক শক্তির উদ্ভব হয়, তার সংখ্যাগত মান কুলী দুটির পারস্পরিক আবেশাঙ্কের সমান। M-এর একক L-এর এককের অনুরূপ; অর্থাৎ হেনরি (henry)।

গাণিতিক উদাহরণ

১। ঘনিষ্ঠভাবে জড়ানো 300 পাক বিশিষ্ট একটি কুলীর স্বকীয় আবেশ গুণাঙ্ক 5mh। কুন্ডুলীতে 6×10 7 A তড়িৎপ্রবাহ চালনা করলে কুটুলীর মধ্য দিয়ে অতিক্রান্ত্ চৌম্বক ফ্লাক্স কত?

এখানে,

N = পাক সংখ্যা = 300

L = স্বাবেশ গুণাঙ্ক = 5×10 H

I = তড়িৎ প্রবাহ = 6×103 A

আমরা জানি,

Nφ = LI

φ = LI/N

= (5×10-3 x 6 x 10-3)/300

= 10-7Wb

উ: 10-7 Wb

৪.৪। পাশাপাশি অবস্থিত দুটি কুলীর একটির মধ্য দিয়ে 0.01 S সময়ে তড়িৎ প্রবাহমাত্রা 0 হতে 10A-এ পরিবর্তন করার ফলে অপর কুলীতে 500 V তড়িচ্চালক শক্তি আবিষ্ট হয়। কুলীদ্বয়ের পারস্পরিক আবেশ গুণাঙ্ক কত?

এখানে

ε2 = আবিষ্ট তড়িচ্চালক শক্তি = 500 V

dI1 = প্রবাহমাত্রার পরিবর্তন = ( 10 – 0 ) A = 10A

dt = সময়ের পরিবর্তন = 0.01S.

আমরা জানি, গৌণ কুলীতে আবিষ্ট তড়িচ্চালক শক্তি,

ε2 = -M(dI/dt) = M(dI1/dt) (বিয়োগ চিহ্ন আগ্রাহ্য করে)

বা, M = ε2/(dI1/dt)

M = 500/(10/0.01)

= 500/1000

= 0.5

উ: 0.5 henry

সার-সংক্ষেপ :

স্বকীয় আবেশ:

কোনো বর্তনীর নিজ প্রবাহের দ্বারা-সৃষ্ট চৌম্বক ক্ষেত্রের মাত্রা পরিবর্তনের ফলে বর্তনীতে একটি তড়িচ্চালক শক্তি আবিষ্ট হয়। এ ঘটনাকে স্বকীয় আবেশ বলা হয়।

স্বকীয় আবেশ গুণাঙ্ক :

কোনো কুলীতে একক তড়িৎ প্রবাহিত হলে কুলীতে সংযুক্ত মোট চৌম্বক ফ্লাক্সকে ঐ কুলীর স্বকীয় আবেশ গুণাঙ্ক বলে। এর একক হেনরী ( henry).

পারস্পরিক আবেশ:

পাশাপাশি স্থাপিত দুটি কুলীর যেকোনো একটিতে তড়িৎ প্রবাহের পরিবর্তন ঘটলে অপরটিতে তড়িচ্চালক শক্তি আবিষ্ট হয়। এ ঘটনাকে পারস্পরিক আবেশ বলে।

পারস্পরিক আবেশ গুণাঙ্ক :

দুটি কুলীর মধ্যে একটির মধ্য দিয়ে প্রবাহমাত্রার পরিবর্তনের হার একক হলে দ্বিতীয় কুলীতে যে তড়িচ্চালক শক্তির উদ্ভব হয়, তার সংখ্যাগত মান কুলী দুটির পারস্পরিক আবেশ গুণাঙ্কের সমান।

বহুবিনাচনি প্রশ্নঃ

১। স্বকীয় আবেশ গুণাঙ্ক-

ক. L = –ε/(dI/dt)

খ. L = –(dI/dt)/ε

গ. L = –ε/(dI/dt)

ঘ. L = (dI/dt)/ε

২। 1 henry নিচের কোনটির সমান?

ক. 1VAS-1

খ. 1VS-1A-¹

গ. IVSA-¹

ঘ. 1ASV-1

৩। পারস্পরিক আবেশ গুণাঙ্ক :

ক. M = N2φ2/I1

খ. M = φ2I1/N2

গ. M = N2I1/φ2

ঘ. M = N2φ2I1

৪। কোনো কুলীতে তড়িৎ প্রবাহের হার 40A s হলে 8V তড়িচ্চালক শক্তি আবিষ্ট হয়। কুলীর স্বকীয় আবেশ গুণাঙ্ক-

ক. 5 H

খ. 0.5 H

গ. 0.2 H

ঘ. 2 H